Integrales que contienen potencias de secante y tangente
La potencia de la secante es par y positiva (2n) conservamos un factor de sec2x y se usa la fórmula sec2x = 1 + tg2x para expresar los demás factores en términos de tg x :
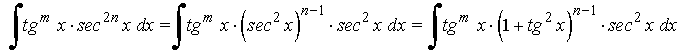
Ejemplo:
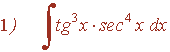
![]()
![]()
![]()
La potencia de la tangente es impar y positiva (2m+1) conservamos un factor de sec x·tg x y se usa la fórmula tg2x = sec2x - 1 para expresar los demás factores en términos de sec x :
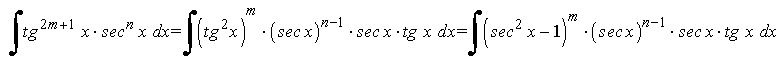
Ejemplo:
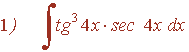
![]()
![]()
![]()
![]()
La potencia de la tangente es par y positiva (2m) y no hay secante convertimos un factor tg2x en términos de sec2x . Se desarrolla y se repite si es necesario:
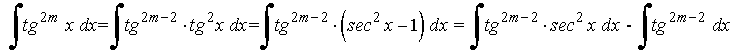
Ejemplo:
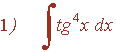
![]()
![]()
![]()
La potencia de la tangente es impar y positiva (2m+1) y no hay secante convertimos un factor tg2x en términos de sec2x . Se desarrolla y se repite si es necesario:
Ejemplo:
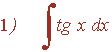
![]()
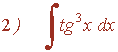
![]()
![]()
![]()
La potencia de la secante es impar y positiva (2n+1) y no hay tangente se resuelve por partes:
Ejemplo:
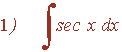
![]()
![]()
![]() Haga click para ir al resultado
Haga click para ir al resultado
Las siguientes integrales se pueden considerar inmediatas a partir de la deducciones anteriores:
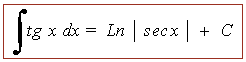
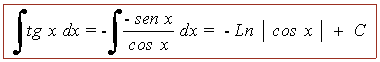
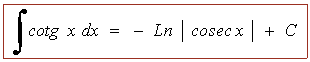
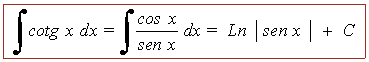
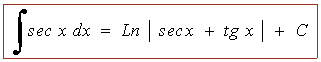
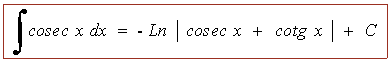


 INICIO
INICIO

