Ejercicios resueltos de integrales trigonométricas inmediatas I
Haga click en la correspondiente pestaña para ver la solución del ejercicio
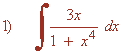
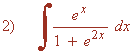
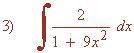
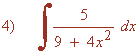
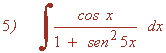
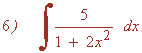
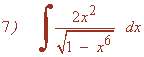
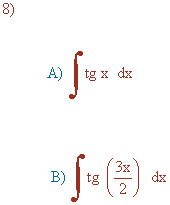
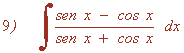
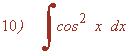
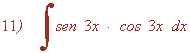
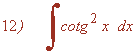
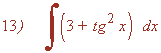
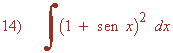
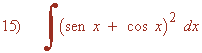
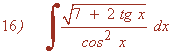
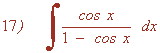
Ejercicios resueltos de integrales trigonométricas inmediatas II
Nota de clase
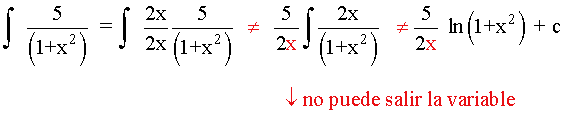
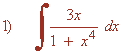
Observamos que la integral es muy parecida a la integral inmediata para el arcotangente.
Ver tabla de integrales inmediatas.
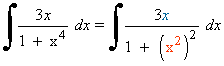
Observamos que la derivada de la función u=x2 es u'=2x , buscaremos tener dicha derivada dentro de la integral para aplicar directamente la regla para el arcotangente.
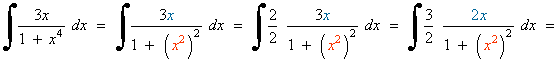
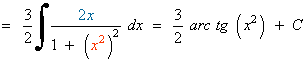
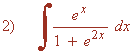
Observamos que la integral es muy parecida a la integral inmediata para el arcotangente.
Observamos que la derivada de la función u=ex es u'=ex , como tenemos la derivada dentro de la integral podemos aplicar directamente la regla para el arcotangente.
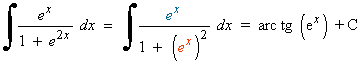
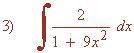
Operando un poco sobre la función observamos que la integral es muy parecida a la integral inmediata para el arcotangente.
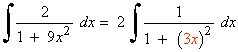
La derivada de la función u=3x es u'=3 , buscaremos tener dicha derivada dentro de la integral para aplicar directamente la regla para el arcotangente. Para ello multiplicamos por:
![]()
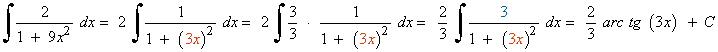
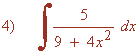
Operando un poco sobre la función observamos que la integral es muy parecida a la integral inmediata para el arcotangente.
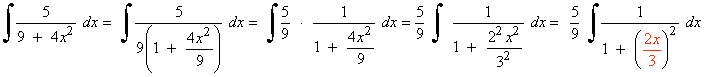
La derivada de la función u=2x/3 es u'=2/3 , buscaremos tener dicha derivada dentro de la integral para aplicar directamente la regla para el arcotangente. Para ello multiplicamos por:
![]()
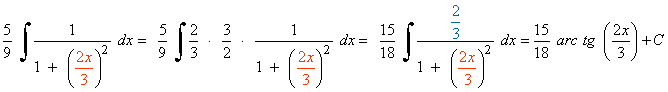
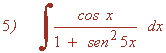
La integral es muy parecida a la integral inmediata para el arcotangente.
La derivada de la función u = sen 5x es u' = 5 cos 5x . Buscaremos tener dicha derivada dentro de la integral para aplicar la regla del arcotangente.
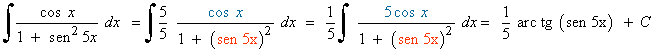
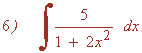
La integral es muy parecida a la integral inmediata para el arcotangente.
Se observa que 2 = (√2)2 , por lo que sustituimos en la integral.
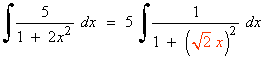
La derivada de la función u = √2x es u' = √2 . Multiplicamos por:
![]()
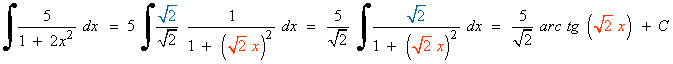
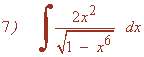
La integral es muy parecida a la integral inmediata para el arcoseno.
Se observa que x6 = (x3)2 , por lo que sustituimos en la integral.
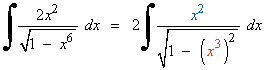
La derivada de la función u = x3 es u' = 3x2 , así que multiplicamos por:
![]()
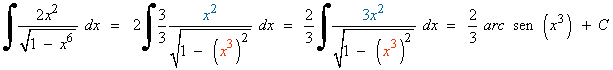
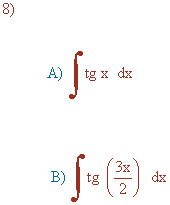
A) De más fácil a más complicada por tres métodos:
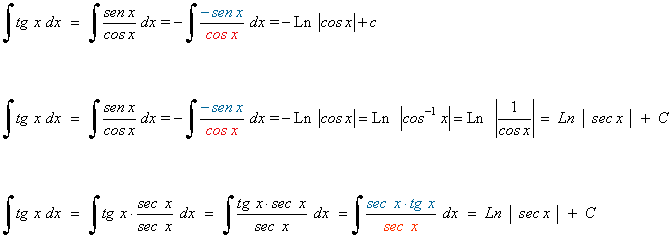
B)
La derivada de u = 3x/2 es u' = 3/2 . Multiplicamos por:
![]()
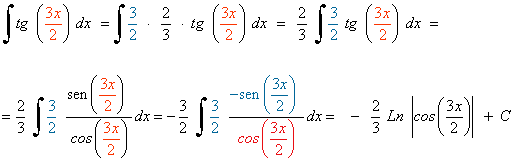
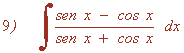
La derivada de u = sen x + cos x es u' = cos x - sen x . Buscaremos tener dicha derivada dentro de la integral para poder aplicar directamente la regla para el logaritmo.
Para ello multiplicamos por:
![]()
![]()
![]()
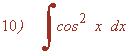
Aplicamos la fórmula de reducción de potencias para el coseno:
![]()
Ver página de fórmulas trigonométricas.
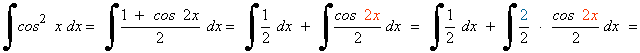
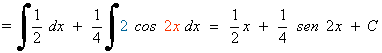
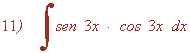
La derivada de la función u = sen 3x es u' = 3 cos 3x . Buscaremos tener dicha derivada dentro de la integral para poder aplicar la regla de la potencia. Para ello multiplicamos por:
![]()
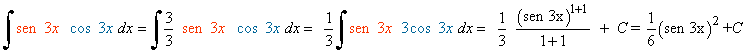
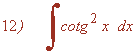
Podemos resolverla como una integral inmediata aplicando la fórmula para 1 + cotg2x . Tan sólo nos falta un +1 dentro de la integral.
Ver tabla de integrales inmediatas.
Restamos y sumamos la unidad dentro de la integral: - 1 + 1 = 0
![]()
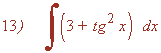
Podemos resolverla como una integral inmediata aplicando la fórmula para 1 + tg2x . Tan sólo nos falta un +1 dentro de la integral.
Ver tabla de integrales inmediatas.
Descomponemos el 3 en dos sumandos: 3 = 2 + 1
![]()
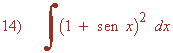
Descomponemos la integral:
![]()
La única integral que no es inmediata es la tercera, así que vamos a calcularla por separado
Para ello vamos a aplicar la fórmula trigonométrica para la reducción de potencias:
![]()
Ver página de fórmulas trigonométricas.
![]()
![]()
Terminamos de calcular nuestra integral:
![]()
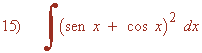
Descomponemos la integral realizando el cuadrado del binomio:
![]()
Aplicamos la fórmula fundamental de la trigonometría sen2 + cos2 =1 , y la fórmula del ángulo doble sen 2x = 2 sen x cos x .
Ver página de fórmulas trigonométricas.
![]()
![]()
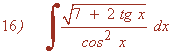
Escribimos la raíz en forma de potencia, aplicamos la fórmula de la secante.
![]()
Ver página de relaciones trigonométricas.
![]()
Observamos que: u = 7 + 2 tg x → u' = 2 sec2x
Buscaremos tener dicha derivada dentro de la integral para aplicar directamente la regla de la potencia. Para ello multiplicamos por:
![]()
![]()
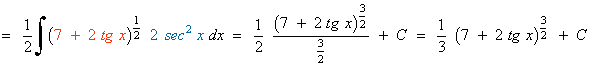
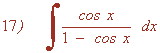
Multiplicamos por el conjugado del denominador (1 + cos x) y operamos:
![]()
Aplicamos la fórmula fundamental de la trigonometría sen2x + cos2x = 1 y descomponemos:
Ver página de fórmulas trigonométricas.
![]()
![]()
En la primera integral observamos que la derivada de u = sen x es u' = cos x , por lo que podemos aplicar directamente la regla de la potencia. Las otras dos integrales son inmediatas.
Ver tabla de integrales inmediatas.
![]()
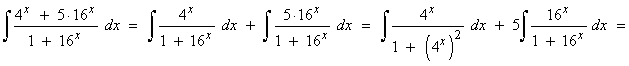
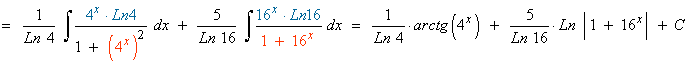


 INICIO
INICIO