Límites de una función en el infinito
Límites finitos en el infinito. Asíntota horizontal.
El límite de una función f(x) cuando x tiende a + ∞ , es un número real L cuando para valores muy grandes de x los valores de la función se aproximan al número L .
De manera más precisa, diremos que la función f(x) tiene por límite L cuando x → +∞ y lo representamos por:
![]()
si dado un ε > 0 existe un h tal que si x > h entonces | f(x) - L | < ε .
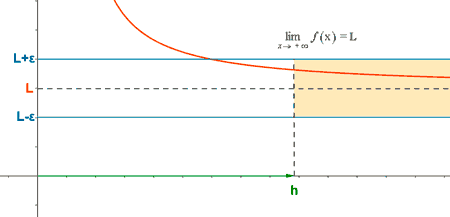
La función f tiene una asíntota horizontal en y = L .
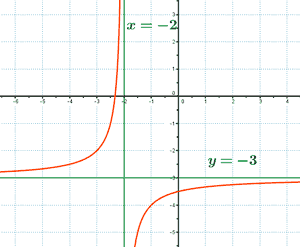
Ejemplo de asíntota horizontal
![]()
![]()
Límites infinitos en el infinito
Cuando no existe ningún número real L que verifique la condición anterior, puede suceder que f(x) → +∞ o ninguna de estas cosas.
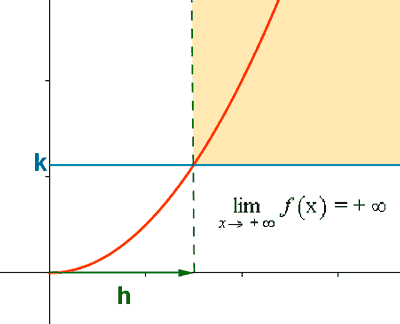
Así, diremos que f(x) → +∞ , y se escribe de la siguiente manera:
![]()
si dado un un número arbitrario K podemos encontrar otro número h tal que si x > h ⇒ f(x) > K .
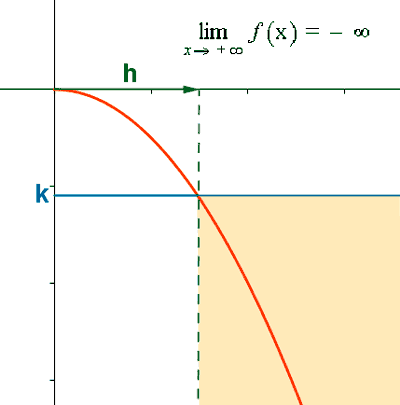
De manera similar podemos definir los siguientes límites:
![]()
Si dado un número arbitrario K podemos encontrar otro número h tal que si x > h ⇒ f(x) < K .
![]()
Si dado un número arbitrario K podemos encontrar otro número h tal que si x < h ⇒ f(x) > K .
![]()
Si dado un número arbitrario K podemos encontrar otro número h tal que si x < h ⇒ f(x) < K .
Ejemplos de límites ínfinitos en el infinito
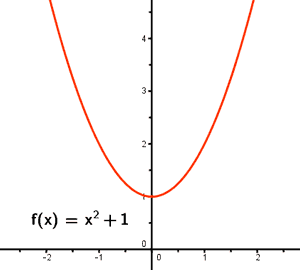
Si x toma valores muy grandes, la función f(x) toma valores tan grandes como queramos.
![]()
Si x toma valores muy pequeños, la función f(x) toma valores tan grandes como queramos.
![]()
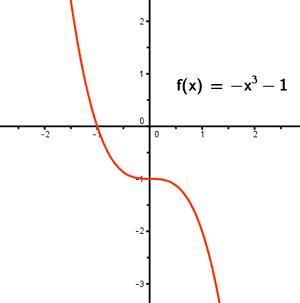
Si x toma valores muy grandes, la función f(x) toma valores tan pequeños como queramos.
![]()
Si x toma valores muy pequeños, la función f(x) toma valores tan grandes como queramos.
![]()
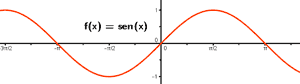
Aunque x tome valores grandes o muy pequeños, la función f(x) no tiende a ningún valor en concreto, ni crece ni disminuye indefinidamente.
![]()


 INICIO
INICIO

