Definición de límite de una función en un punto

La definición de límite de una función en un punto es la siguiente:

Se lee:    "El límite de la función   f(x)   cuando   x   tiende a   a   es igual a   L" .

Es equivalente a decir que para todo número épsilon (ε) mayor que cero, existe un número delta (δ), también mayor que 0, tal que para todo valor de   x   que cumpla que su diferencia con a, en valor absoluto, sea mayor que 0 y menor que delta, se cumple que la diferencia entre f(x) y L, también en valor absoluto, es menor que el número épsilon elegido.

También se puede concretar la definición anterior:

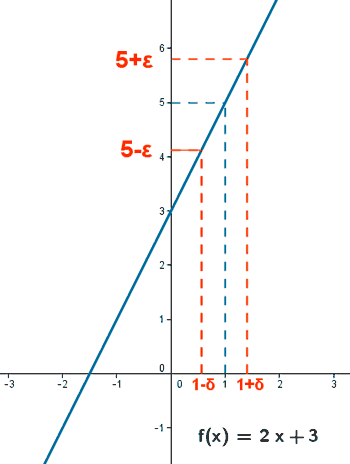
Una función   f(x)   tiende hacia   L   en un punto   a   cuando para todo entorno de   L   de radio   ε ,  E(L, ε) = (L - ε, L + ε) ,  hay un entorno de   a   de radio   δ ,  E(a, δ) = (a - δ, a + δ)  tal que para cualquier   x   de   E(a, δ)   su imagen   f(x)   está en   E(L, ε) .

Ejemplo de calculo de límite aplicando la definición:

Es decir, dado   ε > 0 ,  hay que ver que   |f(x) - L| < ε   siempre que   |x - a| < δ .

En nuestro caso   |(2x + 3) - 5| < ε      siempre que   |x - 1| < δ .

Como   |(2x + 3) - 5| < ε   ⇔   |2x - 2| < ε   ⇒   - ε < 2x - 2 < ε

Tenemos por lo tanto que:   - ε + 2 < 2x < ε + 2

Transformando la desigualdad llegamos a:

Por lo tanto, hemos demostrado que:

Por ejemplo, si tomamos   ε = 0,002, habrá que tomar valores de   x   que se distancien de   1   menos de   δ = 0,002 / 2 = 0,001 .  Es decir, valores de   x   tales que:   0,999 < x < 1,001