Límites laterales de una función en un punto
El límite de una función f(x) , cuando x tiende a un punto a por la izquierda , es un número real L1 , cuando para valores de x muy próximos a a y menores que a , los valores de la función se aproximan al número L1 .
De manera más precisa, diremos que la función f(x) tiene por límite L1 cuando x → a - y lo representamos por:
![]()
si para todo ε > 0 existe un δ > 0 tal que si 0 < a - x < δ entonces se tiene que |f(x) - L1| < ε
El límite de una función f(x) , cuando x tiende a un punto a por la derecha , es un número real L2 , cuando para valores de x muy próximos a a y mayores que a , los valores de la función se aproximan al número L2 .
De manera más precisa, diremos que la función f(x) tiene por límite L2 cuando x → a + y lo representamos por:
![]()
si para todo ε > 0 existe un δ > 0 tal que si 0 < x - a < δ entonces se tiene que |f(x) - L2| < ε
Límite de una función en un punto
El límite de una función en un punto existe si, y sólo si, existen los dos límites laterales en dicho punto y ambos coinciden.
![]()
Para que exista el límite de una función en x = a , tienen que existir los límites laterales y han de ser iguales.
Ejemplo de límite lateral de una función:
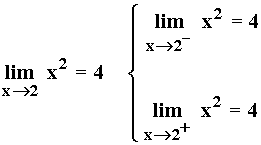
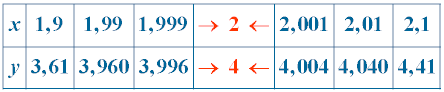
Cuando la variable independiente x se aproxima a 2 , tanto por la izquierda como por la derecha, la variable dependiente y se aproxima a 4 .
Hallar los límites laterales de la siguiente función a trozos en el punto de corte.
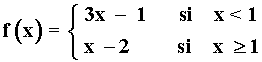
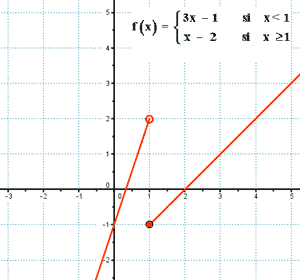
![]()
![]()
Los límites laterales existen pero no coinciden, por tanto:
![]()


 INICIO
INICIO

