Ejercicios de funciones exponenciales y logarítmicas
Resumen de las propiedades de la función exponencial ex
| 1 | La función exponencial es la inversa de la logarítmica: y = ex ⇔ x = Ln y |
|---|---|
| 2 | La función y = ex tiene por dominio R y por recorrido y > 0 |
| 3 | La función y = ex es continua, creciente e inyectiva en todo su dominio. |
| 4 | La función y = ex es cóncava hacia arriba en todo su dominio. |
| 5 | |
Resumen de las propiedades de la función logaritmo neperiano
| 1 | La función logarítmica es la inversa de la exponencial: y = Ln x ⇔ x = ey |
|---|---|
| 2 | La función y = Ln x tiene por dominio { x ∈ R | x > 0 } y por recorrido R . |
| 3 | La función y = Ln x es continua, creciente e inyectiva en todo su dominio. |
| 4 | La función y = Ln x es convexa o cóncava hacia abajo en todo su dominio. |
| 5 | |
Dadas las siguientes funciones, estudia todas sus características e indica sus asíntotas. Representa su gráfica.
f(x) = 2x g(x) = 2 - x = (1/2)x
1) Dominio:
El dominio de las funciones exponenciales es R.
Dom(f) = Dom(g) = R .
2) Recorrido:
El recorrido de las funciones exponenciales es (0, + ∞) .
Im(f) = Im(g) = (0, + ∞) .
3) Puntos de corte:
f(0) = 20 = 1 , el punto de corte con el eje Y es (0, 1).
g(0) = - 20 = 1 , el punto de corte con el eje Y es (0, 1).
La funciones f(x) y g(x) no cortan al eje X.
4) Crecimiento y decrecimiento:
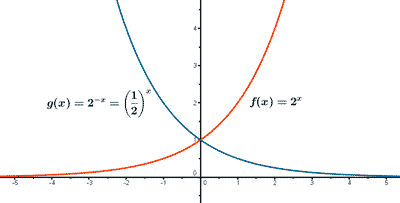
La función f(x) es creciente ya que a > 1 .
La función g(x) es decreciente ya que 0 < a < 1 .
5) Concavidad y convexidad:
Las funciones f(x) y g(x) son concavas.
6) Asíntotas:
Las funciones f(x) y g(x) tienen una asintota en el eje X.
7) Tabla de valores:
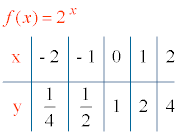
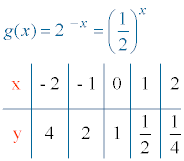
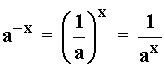
Dada la siguiente función, estudia todas sus características e indica sus asíntotas. Representa su gráfica.
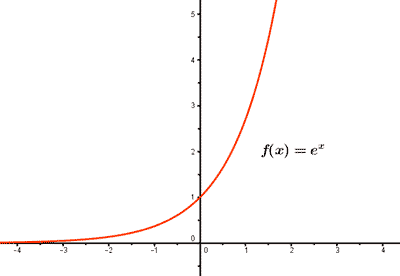
f(x) = ex
1) Dominio:
El dominio de las funciones exponenciales es R.
Dom(f) = R .
2) Recorrido:
El recorrido de las funciones exponenciales es (0, + ∞) .
Im(f) = (0, + ∞) .
3) Puntos de corte:
f(0) = e0 = 1 , el punto de corte con el eje Y es (0, 1).
La función f(x) no corta al eje X.
4) Crecimiento y decrecimiento:
La función f(x) es creciente ya que e > 1 .
5) Concavidad y convexidad:
Las función f(x) es concava.
6) Asíntotas:
Las función f(x) tiene una asintota en el eje X.
7) Tabla de valores:
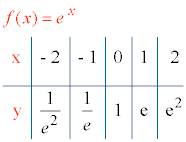
Dada la siguiente función, estudia todas sus características e indica sus asíntotas. Representa su gráfica.
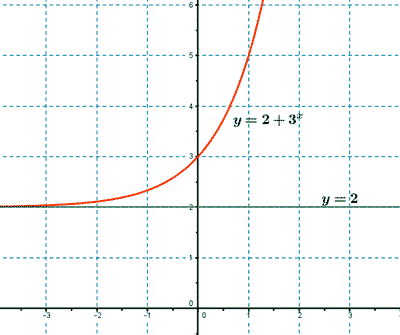
y = 2 + 3x
1) Dominio:
El dominio de las funciones exponenciales es R.
2) Recorrido:
Esta función es una traslación vertical de la función exponencial f(x) = 3x, cuyo recorrido es (0 , ∞).
Por tanto su recorrido queda trasladado verticalmente en dos unidades: (2, + ∞) .
3) Puntos de corte:
y = 2 + 30 = 2 + 1 = 3 , el punto de corte con el eje Y es (0, 3).
La función no corta al eje X.
4) Crecimiento y decrecimiento:
La función es creciente ya que a = 3 > 1 ( y = ax ).
5) Concavidad y convexidad:
Es cóncava por ser una función exponencial.
6) Asíntotas:
Esta función es una traslación vertical de la función exponencial f(x) = 3x, cuya asíntota está en el eje X.
Por tanto la asíntota de nuestra función queda trasaladada verticalmente a la recta y = 2 .
7) Tabla de valores:
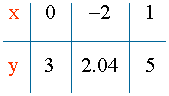
Dada la siguiente función, estudia todas sus características e indica sus asíntotas. Representa su gráfica.
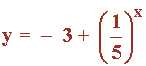
1) Dominio:
El dominio de las funciones exponenciales es R.
2) Recorrido:
Esta función es una traslación vertical de la función exponencial f(x) = (1/5)x, cuyo recorrido viene dado por (0 ,∞).
Por tanto, el recorrido de nuestra función queda trasladado verticalmente -3 unidades: (-3, + ∞) .
3) Puntos de corte:
Punto de corte con el eje Y:
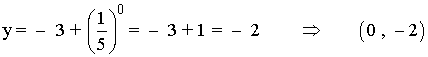
Punto de corte con el eje X:
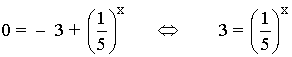
Aplicamos logaritmo en ambos miembros de la igualdad
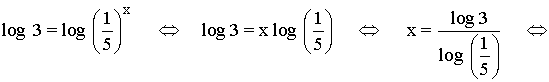
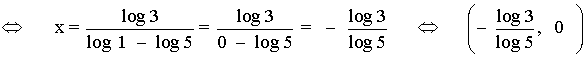
4) Crecimiento y decrecimiento:
La función es decreciente ya que a = 1/5 < 1 ( y = ax ).
5) Concavidad y convexidad:
Es cóncava por ser una función exponencial.
6) Asíntotas:
Esta función es una traslación vertical de la función exponencial f(x) = (1/5)x, cuya asíntota está en el eje X.
Por tanto la asíntota de nuestra función queda trasaladada verticalmente hacia abajo a la recta y = - 3.
7) Tabla de valores:
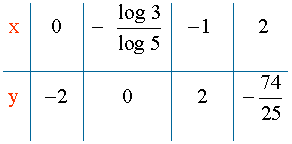
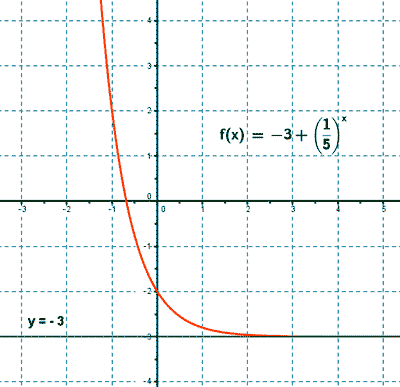
Dada la siguiente función, estudia sus características e indica sus asíntotas. Representa su gráfica.
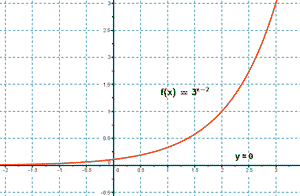
1) y = 3x - 2
Esta función es una traslación horizontal hacia la derecha de la función exponencial g(x) = 3x, es decir, nuestra función es:
f(x) = 3x - 2 = g(x - 2)
Punto de corte con el eje Y:
y = 30 - 2 = 3-2 = 1/9 ⇒ (0 , 1/9)
No corta al eje X.
La función g tiene su asíntota en el eje X.
Como nuestra función es una traslación horizontal de g (no vertical), su asíntota será la misma que la de g.
Por tanto, nuestra función tiene una asíntota en el eje X.
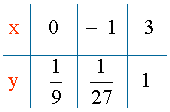
Dadas las siguientes funciones, estudia todas sus características e indica sus asíntotas. Representa su gráfica.
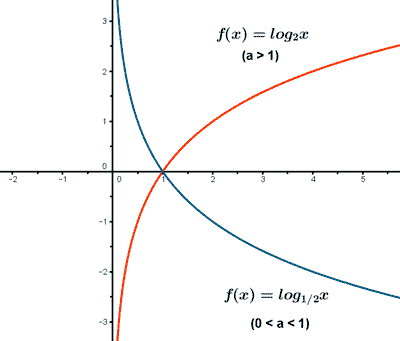
f(x) = log2x g(x) = log1/2x
![]()
1) Dominio:
El dominio de las funciones logarítmicas es (0, + ∞) .
Dom(f) = Dom(g) = (0, + ∞) .
2) Recorrido:
El recorrido de las funciones logarítmicas es R.
Im(f) = Im(g) = R .
3) Puntos de corte:
f(1) = log21 = 0 , el punto de corte con el eje X es (1, 0).
g(1) = log1/21 = 0 , el punto de corte con el eje X es (1, 0).
La funciones f(x) y g(x) no cortan al eje Y.
3) Crecimiento y decrecimiento:
La función f(x) es creciente ya que a > 1 .
La función g(x) es decreciente ya que 0 < a < 1 .
4) Concavidad y convexidad:
Las función f(x) es convexa ya que a > 1 .
Las función g(x) es concava ya que 0 < a < 1 .
5) Asíntotas:
Las funciones f(x) y g(x) tienen una asintota en el eje Y.
6) Tabla de valores:
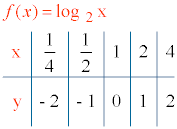
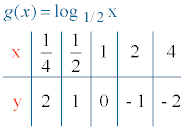
Dada la siguiente función, estudia todas sus características e indica sus asíntotas. Representa su gráfica.
f(x) = ln x
La función logarítmo neperiano es la inversa de y = ex .
Su gráfica es simétrica de y = ex respecto a y = x .
y = ex
x = ey
Por definición: y = ln x
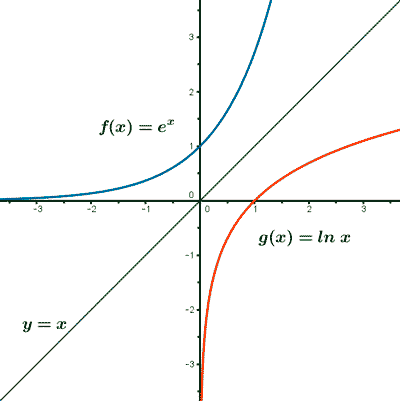
Dada la siguiente función, estudia todas sus características e indica sus asíntotas. Representa su gráfica.
y = 2 + log2 (x - 3)
1) Dominio:
Esta función es una traslación de la función logarítmica g(x) = log2x.
Por un lado, está traslada verticalmente en 2 unidades, y por otro, está trasladada horizontalmente hacia la derecha en 3 unidades. Es decir, nuestra función es:
f(x) = 2 + log2 (x - 3) = 2 + g(x - 3)
El dominio de g es (0 , ∞) , por tanto, el dominio de nuestra función es: (3 , ∞)
2) Recorrido:
Su recorrido viene dado por todos los números reales: R
3) Puntos de corte:
No corta al eje Y, ya que x = 0 no está en el dominio de la función: 0 ∉ (3 , ∞).
Punto de corte con el eje X:
0 = 2 + log2 (0 - 3) = 2 + log2 3 ⇒ ( 2 + log2 3 , 0)
4) Crecimiento y decrecimiento:
La función es creciente ya que a = 2 > 1 ( y = loga x) .
5) Concavidad y convexidad:
La función es convexa ya que a = 2 > 1 ( y = loga x) .
6) Asíntotas:
La función g(x) = log2 x tiene una asíntota en el eje Y.
Como nuestra función está trasladada horizontalmente hacia la derecha en 3 unidades con respecto a la función g , su asíntota también queda trasladada de la misma forma.
Por tanto, nuestra función tiene una asíntota vertical en x = 3 .
7) Tabla de valores:
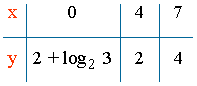
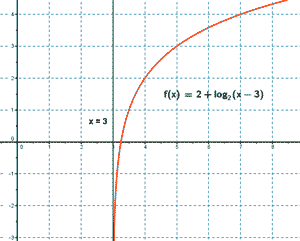
Dada la siguiente función, estudia todas sus características e indica sus asíntotas. Representa su gráfica.
y = - 3 + log1/2 (x + 2)
Esta función es una traslación de la función logarítmica g(x) = log1/2x.
Por un lado, está traslada verticalmente en -3 unidades, y por otro, está trasladada horizontalmente hacia la izquierda en 2 unidades. Es decir, nuestra función es:
f(x) = - 3 + log1/2 (x + 2) = - 3 + g(x + 2)
Punto de corte con el eje Y:
y = - 3 + log1/2 (0 + 2) = - 3 + log1/2 2 = - 3 + (-1) = - 4 ⇒ (0 , - 4)
Punto de corte con el eje X:
![]()
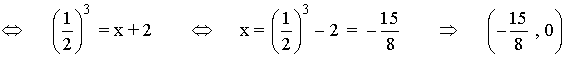
La función g tiene su asíntota en el eje Y.
Como nuestra función está trasladada horizontalmente hacia la izquierda en 2 unidades con respecto a la función g , su asíntota estará trasladada de la misma forma.
Por tanto, nuestra función tiene una asíntota vertical en x = -2 .
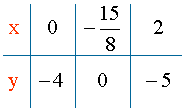
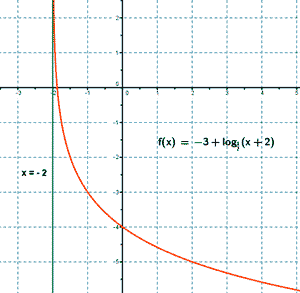


 INICIO
INICIO