Ejercicios de funciones a trozos II
Representa la siguiente función con todas sus características: y = Ent(x) + 3
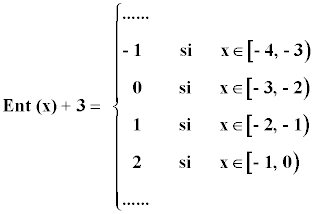
f (- 1) = Ent (- 1) + 3 = - 1 + 3 = 2
f (- 0,9) = Ent (- 0,9) + 3 = - 1 + 3 = 2
f (- 0,1) = Ent (- 0,1) + 3 = - 1 + 3 = 2
f (0,1) = Ent (0,1) + 3 = 0 + 3 = 3
f (0,9) = Ent(0,9) + 3 = 0 + 3 = 3
f (1) = Ent(1) + 3 = 1 + 3 = 4
f (1,1) = Ent(1,1) + 3 = 1 + 3 = 4
Dom(f) = R
Im(f) = Z
Ent(x) + 3 = { n + 3 si x ∈ [n , n+1) con n ∈ Z}
Puntos de corte:
• Para x = 0 tenemos que f(0) = 3 ⇒ El punto de corte es (0, 3)
• Para que f(x) = 0 ⇒ Ent(x) + 3 = 0 ⇒ Ent(x) = - 3 ⇒ Los puntos de corte son todos los puntos del intervalo [- 3, -2) .
Monotonía:
La función parte entera siempre toma valores constantes, por lo tanto no es creciente ni decreciente.
Máximos y mínimos:
No tiene máximos ni mínimos.
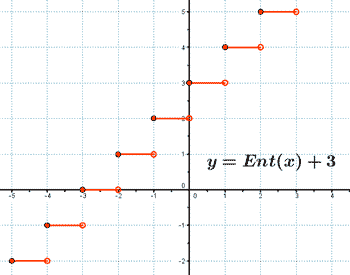
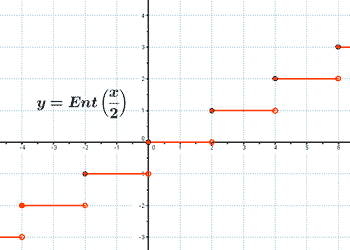
Representa la siguiente función con todas sus características: y = Ent(x/2)
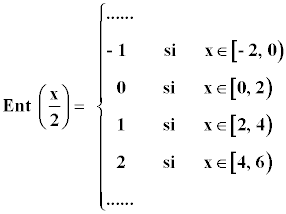
f (- 1) = Ent (- 0.5) = - 1
f (- 0,8) = Ent (- 0,4) = - 1
f (- 0,2) = Ent (- 0,1) = - 1
f (0,2) = Ent (0,1) = 0
f (0,8) = Ent(0,4) = 0
f (1) = Ent(0,5) = 0
f (3,6) = Ent(1,8) = 1
Dom(f) = R
Im(f) = Z
Ent(x/2) = { n si x/2 ∈ [n , n+2) con n ∈ Z }
Puntos de corte:
• Para x = 0 tenemos que f(0) = 0 ⇒ El punto de corte es (0, 0)
• Para que f(x) = 0 ⇒ Ent(x/2) = 0 ⇒ Los puntos de corte son todos los puntos del intervalo [0, 2) .
Monotonía:
La función parte entera siempre toma valores constantes, por lo tanto no es creciente ni decreciente.
Máximos y mínimos:
No tiene máximos ni mínimos.
Representa la siguiente función con todas sus características: y = Dec(x) + 2
f (- 3) = Dec(- 3) + 2 = - 3 - Ent(- 3) + 2 = - 3 - (- 3) + 2 = 2
f (- 2,9) = Dec(- 2,9) + 2 = - 2,9 - Ent(- 2,9) + 2 = - 2,9 - (- 3) + 2 = 2,1
f (- 2,1) = Dec(- 2,1) + 2 = - 2,1 - Ent(- 2,1) + 2 = - 2,1 - (- 3) + 2 = 2,9
f (- 0,2) = Dec(- 0,2) + 2 = - 0,2 - Ent(- 0,2) + 2 = - 0,2 - (- 1) + 2 = 2,8
f (0,2) = Dec(0,2) + 2 = 0,2 - Ent(0,2) + 2 = 0,2 - 0 + 2 = 2,2
f (1,2) = Dec(1,2) + 2 = 1,2 - Ent(1,2) + 2 = 1,2 - 1 + 2 = 2,2
f (8,2) = Dec(8,2) + 2 = 8,2 - Ent(8,2) + 2 = 8,2 - 8 + 2 = 2,2
Dom(f) = R
Im(f) = [2, 3)
Puntos de corte:
• Para x = 0 tenemos que f(0) = Dec(0) + 2 = 0 - Ent(0) + 2 = 0 - 0 + 2 = 2 ⇒ El punto de corte es (0, 2)
• Para y = 0 ⇒ Dec(x) + 2 = 0 ⇒ x - Ent(x) + 2 = 0 ⇒ x - Ent(x) ≠ - 2
Monotonía:
La función parte decimal es creciente en todo su dominio.
Máximos y mínimos:
La función tiene mínimos absolutos en todos los puntos de abscisa entera.
La función no tiene ni máximos absolutos ni relativos.
Periodicidad:
La función tiene periodo 1 ya que f(x + 1) = f(x)
Acotación:
La función está acotada superior e inferiormente.
La cota superior es 3 o cualquier número superior a 3.
La menor de todas las cotas superiores recibe el nombre de extremo superior o supremo, que en este caso es 3.
La cota inferior es 2 o cualquier número inferior a 2.
La mayor de todas las cotas inferiores recibe el nombre de extremo inferior o infimo, que en este caso es 2. Además es mínimo porque pertenece a la imagen de la función.
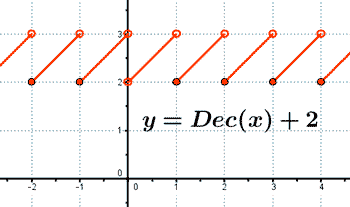
La gráfica corresponde a una traslación vertical hacia arriba dos unidades de la función f(x) = Dec(x)
y = f(x) + 2
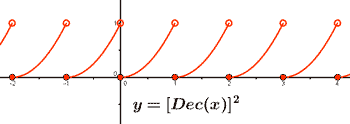
Representa la siguiente función con todas sus características: y = [Dec(x)]2 = [x - Ent(x)]2
f (0) = [Dec(0)]2 = [0 - Ent(0)]2 = 02 = 0
f (0,1) = [Dec(0,1)]2 = [0,1 - Ent(0,1)]2 = (0,1 - 0)2 = (0,1)2 = 0,01
f (0,5) = [Dec(0,5)]2 = [0,5 - Ent(0,5)]2 = (0,5 - 0)2 = (0,5)2 = 0,25
f (0,9) = [Dec(0,9)]2 = [0,9 - Ent(0,9)]2 = (0,9 - 0)2 = (0,9)2 = 0,81
f (1) = [Dec(1)]2 = [1 - Ent(1)]2 = (1 - 1)2 = 02 = 0
f (1,1) = [Dec(1,1)]2 = [1,1 - Ent(1,1)]2 = (1,1 - 1)2 = (0,1)2 = 0,01
Dom(f) = R
Im(f) = [0, 1)
Puntos de corte:
• Para x = 0 tenemos que f(0) = [Dec(0)]2 = [0 - Ent(0)]2 = 02 = 0 ⇒ El punto de corte es (0, 0)
• Para y = 0 ⇒ [Dec(x)]2 = [x - Ent(x)]2 = 0 ⇒ x - Ent(x)= 0 ⇒ x = Ent(x) ⇒ Los puntos de corte son (x, 0) con x ∈ Z
Monotonía:
La función parte decimal es creciente en todo su dominio.
Máximos y mínimos:
La función tiene mínimos absolutos en todos los puntos de abscisa entera.
La función no tiene ni máximos absolutos ni relativos.
Periodicidad:
La función tiene periodo 1 ya que f(x + 1) = f(x)
Acotación:
La función está acotada superior e inferiormente.
La cota superior es 1 o cualquier número superior a 1.
La menor de todas las cotas superiores recibe el nombre de extremo superior o supremo, que en este caso es 1.
La cota inferior es 0 o cualquier número inferior a 0.
La mayor de todas las cotas inferiores recibe el nombre de extremo inferior o infimo, que en este caso es 0. Además es mínimo porque pertenece a la imagen de la función.
Representa las siguientes funciones:
1) y = Dec(x) - 0,5
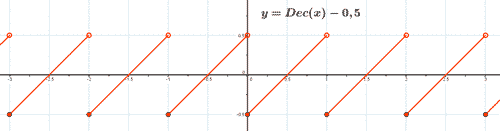
Esta función corresponde a una traslación vertical hacia abajo en 0,5 unidades de la función f(x) = Dec(x)
2) y = |Dec(x) - 0,5|

Esta función transforma los valores negativos de la anterior función en positivos
3) y = 0,5 - |Dec(x) - 0,5| = d(x, Z)

Esta función corresponde a una traslación horizontal hacia la derecha en 0,5 unidades de la función anterior
f (-2) = 0,5 - |Dec(-2) - 0,5| = .......... = 0
f (-1,9) = 0,5 - |Dec(-1,9) - 0,5| = .... = 0,1
f (-1,4) = 0,5 - |Dec(-1,4) - 0,5| = .... = 0,4
f (-0,3) = 0,5 - |Dec(-0,3) - 0,5| = .... = 0,3
f (0,1) = 0,5 - |Dec(0,1) - 0,5| = ....... = 0,1
f (1,1) = 0,5 - |Dec(1,1) - 0,5| = ....... = 0,1
⇒ d(-2, Z) = d(-2, -2) = 0
⇒ d(-1,9, Z) = d(-1,9, -2) = 0,1
⇒ d(-1,4, Z) = d(-1,4, -1) = 0,4
⇒ d(-0,3, Z) = d(-0,3, 0) = 0,3
⇒ d(0,1, Z) = d(0,1, 0) = 0,1
⇒ d(1,1, Z) = d(1,1, 1) = 0,1
Representa las siguientes funciones:
![]()
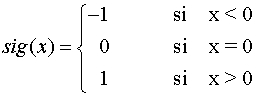
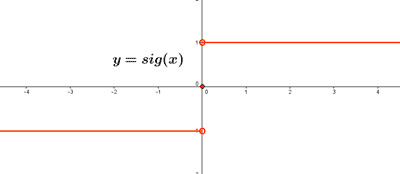
![]()
Escribimos la función dada como una función a trozos:
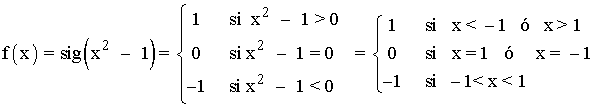
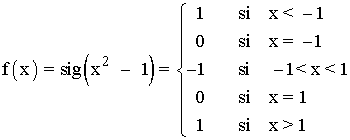
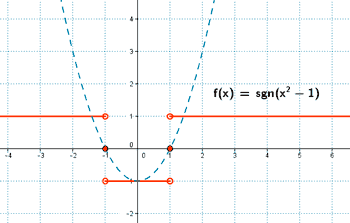


 INICIO
INICIO