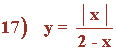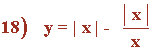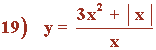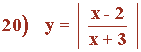Ejercicios de funciones con valor absoluto
Expresa como una función a trozos y dibuja su gráfica:
1) y = |x - 3|
2) y = |x| - 2
4) y = |x| + |x - 2|
5) y = |x + 3| + |x - 3|
6) y = |3x + 1| - |3 - x|
7) y = |x2 - 4|
8) y = | x2 + 2x - 15 |
9) y = |- x2 + 6x - 8|
10) y = |x|2 - 6|x| + 8
11) y = x2 - | x |
12) y = x2 + | x - 2|
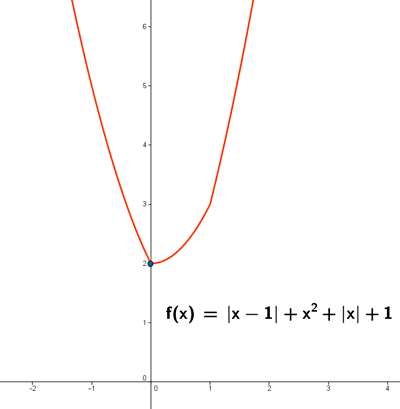
13) y = | x - 1 | + x2 + | x | + 1
14) y = x |x|
15) y = x|x - 4|
16) y = |x| / x
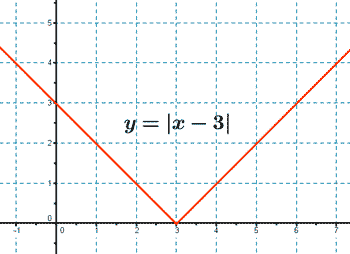
Representa la siguiente función con todas sus características: y = |x - 3|
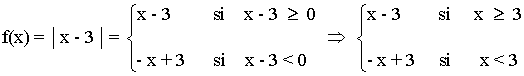
Dom(f) = R
Im(f) = [0, +∞)
Puntos de corte:
• Para x = 0 tenemos que f(0) = 3 ⇒ El punto de corte es (0, 3)
• Para que f(x) = 0 ⇒ 0 = x - 3 ⇒ x = 3 ⇒ El punto de corte es (3, 0)
Monotonía:
• La función es decreciente en el intervalo (-∞, 3) puesto que y = - x + 3 tiene pendiente negativa (m = - 1) .
• La función es creciente en el intervalo (3, +∞) puesto que y = x - 3 tiene pendiente positiva (m = 1) .
Máximos y mínimos:
La función posee un mínimo absoluto en el punto (3, 0) ya que f(x) ≥ 0 para cualquier valor de x .
Representa la siguiente función con todas sus características: y = |x| - 2
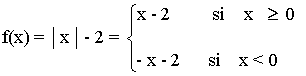
Dom(f) = R
Im(f) = [-2, +∞)
Puntos de corte:
• Para x = 0 tenemos que f(0) = - 2 ⇒ El punto de corte con el eje Y es (0, - 2)
• Para que f(x) = 0 ⇒ 0 = |x| - 2 ⇒ |x| = 2 ⇒ x = ±2 ⇒ Corta al eje X en los puntos (- 2, 0) y (2, 0)
Monotonía:
• La función es decreciente en el intervalo (-∞, 0) puesto que y = - x - 2 tiene pendiente negativa (m = - 1) .
• La función es creciente en el intervalo (0, +∞) puesto que y = x - 2 tiene pendiente positiva (m = 1) .
Máximos y mínimos:
La función posee un mínimo absoluto en el punto (0, - 2) ya que f(x) ≥ - 2 para cualquier valor de x .
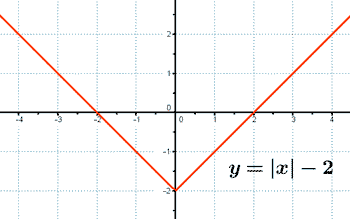
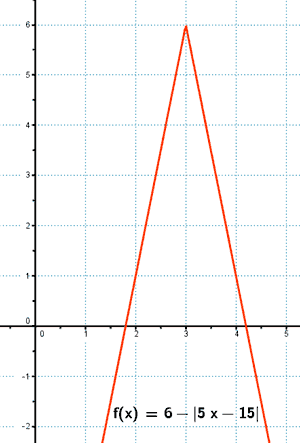
La gráfica es el resultado de trasladar verticalmente hacia abajo dos unidades a la función f(x) = |x|
Es decir, y = f(x) - 2 = |x| - 2
![]()
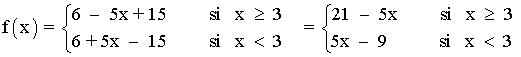
Exprese la siguiente función como una función definida a trozos: f(x) = |x| + |x - 2|
Estudiamos cada valor absoluto por separado:
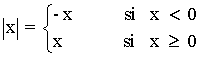
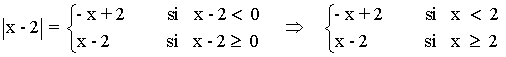
A continuación, estudiamos la suma de los valores de |x| y |x - 2| en los tres intervalos que se generan: (-∞ 0) , (0, 2) y (2, +∞) .
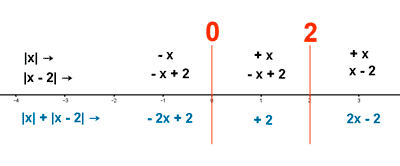
Por lo tanto la función queda definida de la siguiente forma:
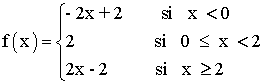
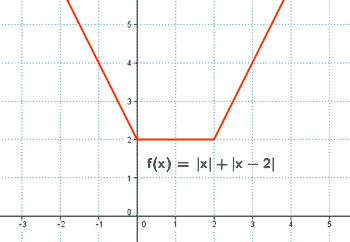
Representa la siguiente función con todas sus características: y = |x + 3| + |x - 3|
Estudiamos cada valor absoluto por separado:
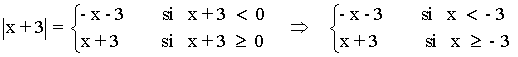
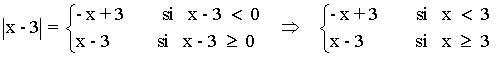
A continuación, estudiamos la suma de los valores de |x + 3| y |x - 3| en los tres intervalos que se generan: (-∞, -3) , (-3, 3) y (3, +∞) .
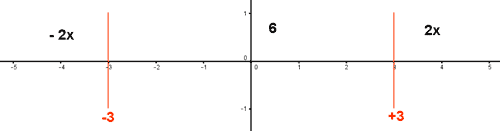
Por lo tanto la función queda definida de la siguiente forma:
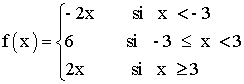
Dom(f) = R
Im(f) = [6 , +∞)
Puntos de corte:
• x = 0 ⇒ f(0) = 6 ⇒ No corta al eje Y
• f(x) = 0 ⇒ - 2x = 0 ⇒ x = 0 ⇒ No corta al eje X puesto que x = 0 no pertenece a dicho intervalo.
⇒ 6 ≠ 0 ⇒ No corta al eje X
⇒ 2x = 0 ⇒ x = 0 ⇒ No corta al eje X puesto que x = 0 no pertenece a dicho intervalo.
Monotonía:
• La función es decreciente en el intervalo (-∞, -3) puesto que y = -2x tiene pendiente negativa (m = -2) .
• La función no es creciente ni decreciente en el intervalo (-3, 3) puesto quees una función constante.
• La función es creciente en el intervalo (3, +∞) puesto que y = 2x tiene pendiente positiva (m = 2) .
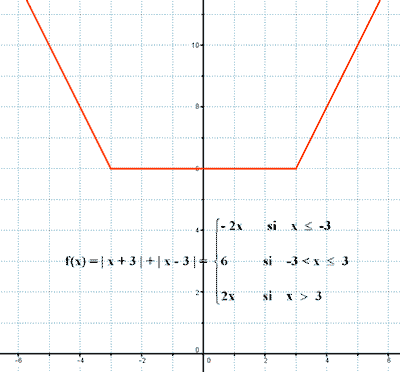
Representa la siguiente función con todas sus características: y = |3x + 1| - |3 - x|
Estudiamos cada valor absoluto por separado:
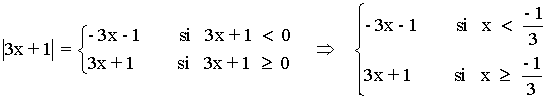
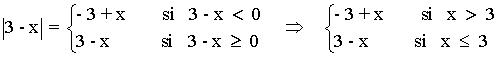
A continuación, estudiamos la suma de los valores de |3x + 1| y |3 - x| en los tres intervalos que se generan: (-∞, -1/3) , (1/3, 3) y (3, +∞) .
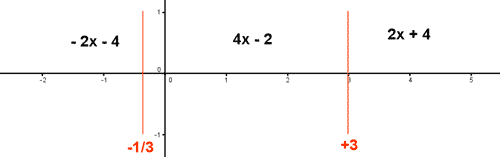
Por lo tanto la función queda definida de la siguiente forma:
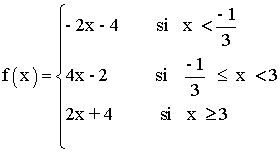
Dom(f) = R
Im(f) = [-10/3 , +∞) puesto que f(-1/3) = 2/3 - 4 = -10/3
Puntos de corte:
• x = 0 ⇒ f(0) = - 2 ⇒ Corta al eje Y en el punto (0 , -2)
• f(x) = 0 ⇒ - 2x - 4 = 0 ⇒ x = - 2 ⇒ Corta el eje X en el punto (-2, 0)
⇒ 4x - 2 = 0 ⇒ x = 1/2 ⇒ Corta al eje X en el punto (1/2, 0)
⇒ 2x + 2 = 0 ⇒ x = - 1 ⇒ No corta al eje X puesto que x = - 1 no pertenece a dicho intervalo.
Por lo tanto, los puntos de corte con el eje X son: (-2, 0) y (1/2, 0).
Monotonía:
• La función es decreciente en el intervalo (-∞, -1/3) puesto que y = -2x - 4 tiene pendiente negativa (m = -2) .
• La función es creciente en el intervalo (-1/3, 3) puesto que y = 4x - 2 tiene pendiente positiva (m = 4) .
• La función es creciente en el intervalo (3, +∞) puesto que y = 2x + 2 tiene pendiente positiva (m = 2) .
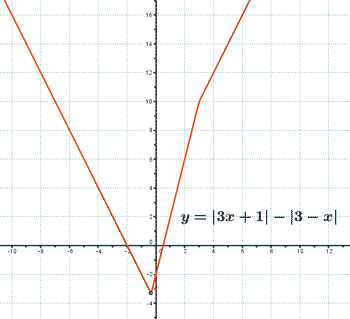
Representa la siguiente función con todas sus características: y = |x2 - 4|
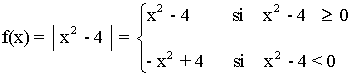
Resolvemos la inecuación: x2 - 4 ≥ 0
x2 - 4 = 0 ⇔ x2 = 4 ⇔ x = √4 ⇔ x = ± 2
A continuación estudiamos el signo en: A = (-∞, -2) B = (-2, 2) C = (2, +∞)
• Intervalo A: x = - 3 ⇒ x2 - 4 = (-3)2 - 4 = 9 - 4 > 0
• Intervalo B: x = 0 ⇒ x2 - 4 = (0)2 - 4 = - 4 < 0
• Intervalo C: x = 3 ⇒ x2 - 4 = (3)2 - 4 = 9 - 4 > 0
Por tanto, tendremos que x2 - 4 ≥ 0 en los intervalos A y C .
Y será x2 - 4 < 0 únicamente en el intervalo B .
La función queda por lo tanto de la siguiente manera:
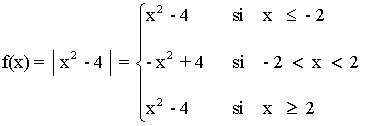
Dom(f) = R
Im(f) = [0, +∞)
Puntos de corte:
• Para x = 0 tenemos que f(0) = 4 ⇒ El punto de corte con el eje Y es (0, 4)
• Para que f(x) = 0 ⇒ Corta al eje X en los puntos (- 2, 0) y (2, 0)
Máximos y mínimos:
La función posee dos mínimos absolutos en los puntos (- 2, 0) y (2, 0) .
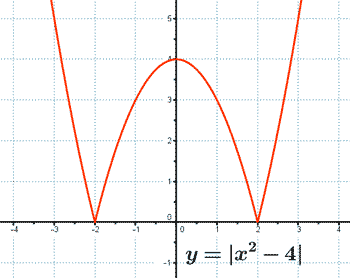
Sea la función: f(x) = | x2 + 2x - 15 |
a) Expresa f(x) como una función definida a trozos
b) Dibuja la gráfica de f(x)
a) Expresa la función f(x) como una función definida a trozos
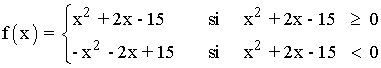
Para definir la función, tenemos que resolver la siguiente ecuación: x2 + 2x - 15 = 0
Las raíces de la ecuación son x = 3 y x = -5 , es decir, tenemos que estudiar como se comporta la función en los siguientes intervalos: (-∞, -5) , (-5, 3) y (3, +∞)
| Intervalo | (-∞, -5) | (-5, 3) | (3, +∞) |
|---|---|---|---|
| Punto de prueba | f(-6) > 0 | f(0) < 0 | f(4) > 0 |
| Signo de f (x) | + | - | + |
Por lo tanto la función queda definida de la siguiente forma:
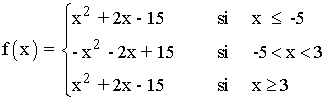
b) Dibuja la gráfica de f(x).
Las funciones que definen a f son polinómicas, por lo que son continuas en todo R , y en particular, lo son en sus intervalos de definición.
A continuación vamos a calcular los puntos de corte:
• Corte con el eje OX: f(x) = 0
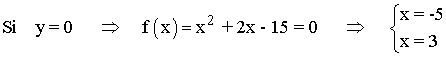
Los puntos de corte son: (-5, 0) y (3, 0)
• Corte con el eje OY: f(0)
![]()
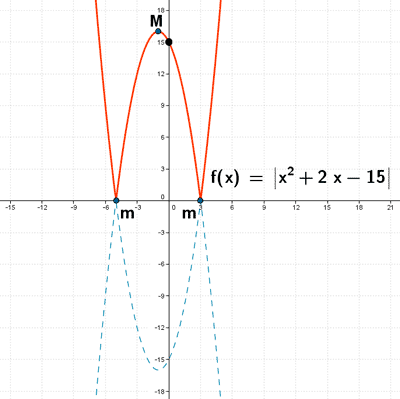
El punto de corte es: (0, 15)
Además, la función tiene un eje de simetría para x = - b / 2a . Es decir, x = -1 .
Para x = -1 tenemos que f(-1) = 16 . Por lo tanto el vértice es el punto V (-1, 16) .
Representa la siguiente función con todas sus características: y = |- x2 + 6x - 8|
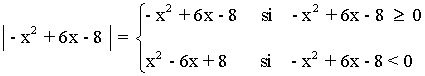
Resolvemos la inecuación: - x2 + 6x - 8 ≥ 0
- x2 + 6x - 8 = 0
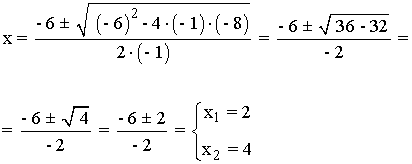
A continuación estudiamos el signo en: A = (-∞, 2) B = (2, 4) C = (4, +∞)
• Intervalo A: x = 0 ⇒ - x2 + 6x - 8 = - 8 < 0
• Intervalo B: x = 3 ⇒ - x2 + 6x - 8 = -(3)2 + 6·3 - 8 = 1 > 0
• Intervalo C: x = 5 ⇒ - x2 + 6x - 8 = -(5)2 + 6·5 - 8 = - 3 < 0
Por tanto, tendremos que - x2 + 6x - 8 ≥ 0 en el intervalo B.
Y será - x2 + 6x - 8 < 0 en los intervalos A y C .
La función queda por lo tanto de la siguiente manera:
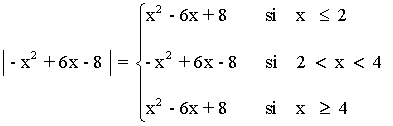
Dom(f) = R
Im(f) = [0, +∞)
Puntos de corte:
• x = 0 ⇒ f(0) = 8 ⇒ El punto de corte con el eje Y es (0, 8)
• f(x) = 0 ⇒ Corta al eje X en los puntos (2, 0) y (4, 0)
Máximos y mínimos:
La función posee dos mínimos absolutos en los puntos (2, 0) y (4, 0) .
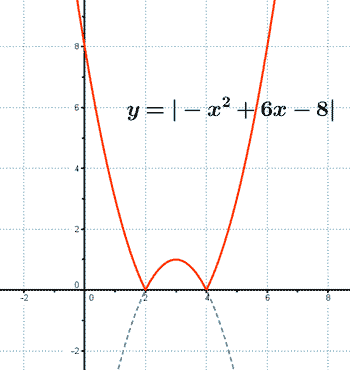
Representa la siguiente función con todas sus características: y = |x|2 - 6|x| + 8
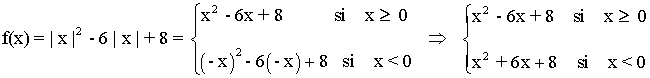
Dom(f) = R
Im(f) = [0, +∞)
Puntos de corte:
• x = 0 ⇒ f(0) = 8 ⇒ Corta al eje Y en el punto (0, 8).
• f(x) = 0 ⇒ x2 - 6x + 8 = 0 ⇒ Las soluciones son -4 y -2.
⇒ x2 + 6x + 8 = 0 ⇒ Las soluciones son 4 y 2
Por lo tanto, los puntos de corte con el eje X son: (-4, 0) (-2, 0) (2, 0) y (4, 0).
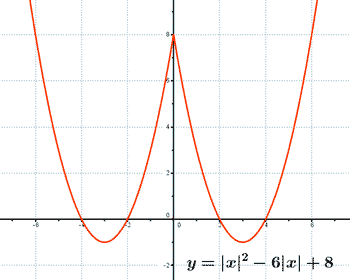
Si f(x) = x2 - 6x + 8 ⇒ f(|x|)= |x|2 - 6|x| + 8
Sea la función: f(x) = x2 - | x |
Vamos a expresarla como una función a trozos:
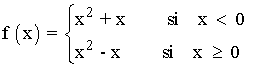
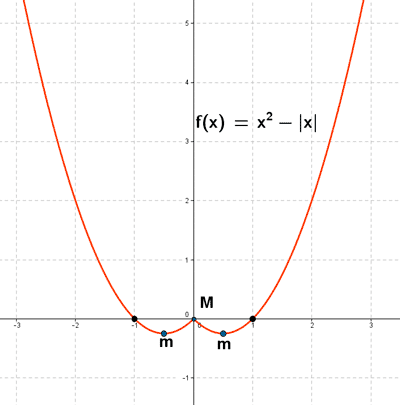
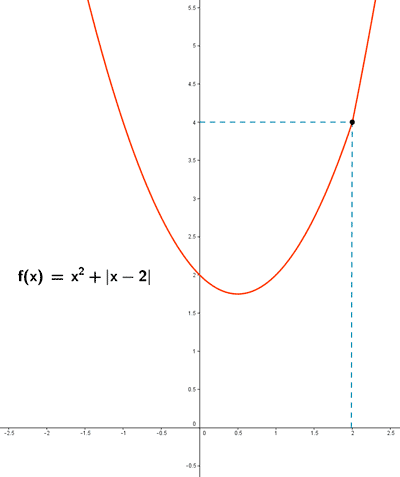
Sea la función: f(x) = x2 + | x - 2|
Definimos la función f por trozos:
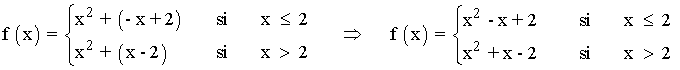
Sea la función: f(x) = | x - 1 | + x2 + | x | + 1
a) Expresa f(x) como una función definida a trozos
b) Representa la función
a) Expresa f(x) como una función definida a trozos
Al tratarse de una función definida como la suma de sumandos con valor absoluto, tenemos que estudiar los intervalos determinados por las soluciones de dichos sumandos:
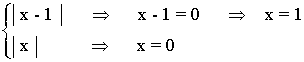
| Intervalo | (-∞, 0) | (0, 1) | (1, +∞) |
|---|---|---|---|
| |x - 1| | - x + 1 | - x + 1 | x - 1 |
| x2 | x2 | x2 | x2 |
| |x| | -x | +x | +x |
| +1 | +1 | +1 | +1 |
| |x - 1|+x2+|x|+1 | x2 - 2x + 2 | x2 + 2 | x2 + 2x |
Por lo tanto, nuestra función queda definida de la siguiente manera:
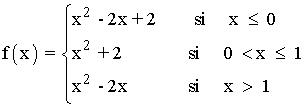
b) Representa la función
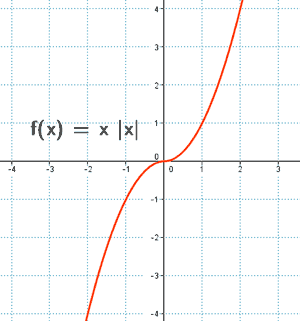
Representa la siguiente función con todas sus características: y = x |x|
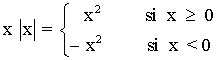
Dom(f) = R
Im(f) = R
Puntos de corte:
• Para x = 0 tenemos que f(0) = 0 ⇒ El punto de corte es (0, 0)
• Para que f(x) = 0 ⇒ 0 = x|x| ⇒ x = 0 ⇒ El punto de corte es (0, 0)
Monotonía:
La función es creciente en todo su dominio, es decir, es creciente en todo R .
Máximos y mínimos:
Como es creciente en todo R , no tiene ni máximos ni mínimos.
Simetría:
f(-x) = - x |-x| = - x |x| = - (x|x|) = - f(x)
Tiene simetría impar.
Funciones pares e impares con valor absoluto
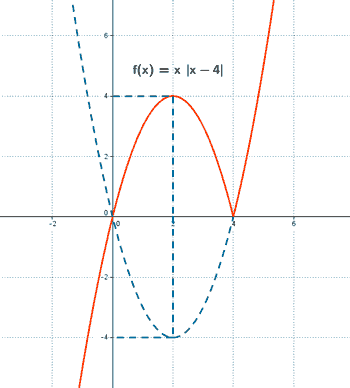
Sea f: R → R la función definida por f(x) = x|x - 4| .
Definimos la función f por trozos:
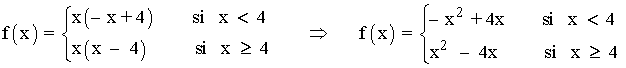
Hallamos los puntos de corte con los ejes:
• Si x = 0 : y = f(0) ⇒ y = 0 ⇒ (0 , 0)
• Si y = 0 : - x2 + 4x = 0 ⇒ x(- x + 4) = 0 ⇒ x = 0 ó x = 4 ⇒ (0 , 0) , (4 , 0)
x2 - 4x = 0 ⇒ x(x - 4) = 0 ⇒ x = 0 ó x = 4 ⇒ (0 , 0) , (4 , 0)
Ambas ramas de f son funciones polinómicas de segundo grado, por lo que son parábolas. Para dibujarlas vamos a calcular sus respectivos vértices:
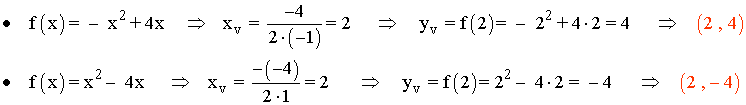
Representa la siguiente función con todas sus características: y = |x| / x
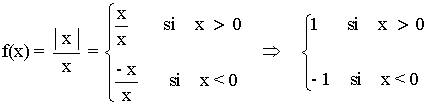
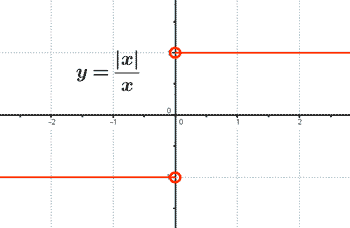
Dom(f) = R - {0}
Im(f) = {-1, 1}
Puntos de corte:
• La función no está definida en x = 0 ⇒ No corta al eje Y.
• f(x) ≠ 0 ⇒ No corta al eje X .
Sea la función:
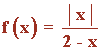
a) Expresa la función f como una función a trozos e indica el dominio de la función.
b) Representa la función.
a) Expresa la función f como una función a trozos e indica el dominio de la función.
Antes de nada, definimos la función f por trozos:
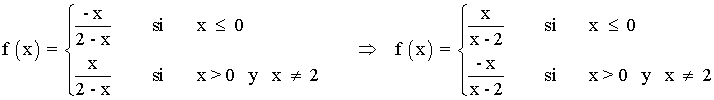
Las funciones que definen a f son racionales, por lo que son continuas excepto en los puntos que se anula el denominador. Por tanto, la función f es continua en: (-∞ , 2) ∪ (2 , ∞)
Dom (f) = R - {2}
d) Representa la función
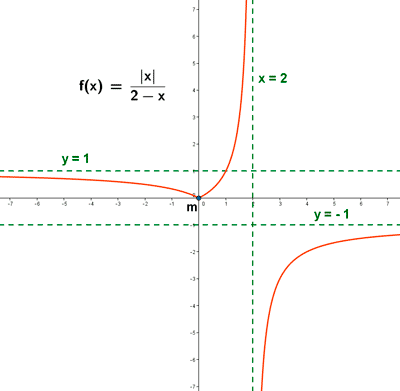
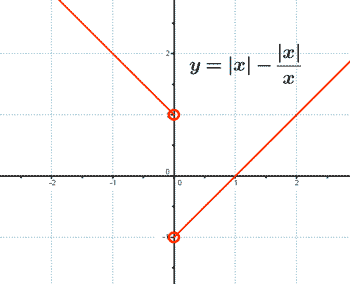
Representa la siguiente función con todas sus características:
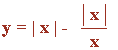
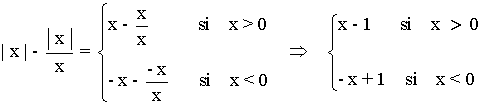
Dom(f) = R - {0}
Im(f) = (-∞, 0) ∪ (0, +∞)
Puntos de corte:
• La función no está definida en x = 0 ⇒ No corta al eje Y.
• f(x) = 0 ⇒ x - 1 = 0 ⇒ x = 1 ⇒ Corta al eje X en el punto (1, 0)
Monotonía:
• La función es decreciente en el intervalo (-∞, 0) puesto que y = - x + 1 tiene pendiente negativa (m = - 1) .
• La función es creciente en el intervalo (0, +∞) puesto que y = x - 1 tiene pendiente positiva (m = 1) .
Representa la siguiente función con todas sus características:
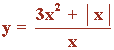
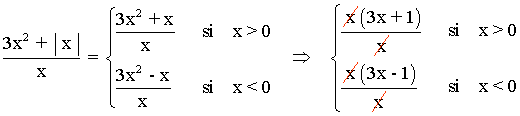
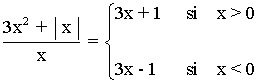
Dom(f) = R - {0}
Im(f) = (-∞, -1) ∪ (1, +∞)
Puntos de corte:
• La función no está definida en x = 0 ⇒ No corta al eje Y.
• f(x) = 0 ⇒ No está definido en el dominio.
Monotonía:
• La función es creciente en el intervalo (-∞, 0) puesto que y = 3x - 1 tiene pendiente positiva (m = 3) .
• La función es creciente en el intervalo (0, +∞) puesto que y = 3x + 1 tiene pendiente positiva (m = 3) .
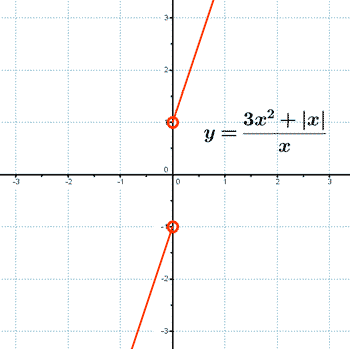
Representa la siguiente función con todas sus características:
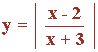
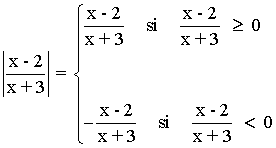
Para estudiar el signo tenemos que resolver las siguientes ecuaciones:
x - 2 = 0 ⇒ x = 2
x + 3 = 0 ⇒ x = - 3
A continuación estudiamos el signo en: A = (-∞, -3) B = (-3, 2) C = (2, +∞)
• Intervalo A: x = - 4 ⇒ f(-4) = 6 > 0
• Intervalo B: x = 0 ⇒ f(0) = - 2/3 < 0
• Intervalo C: x = 4 ⇒ f(4) = 2/5 > 0
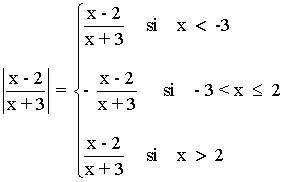
Dom(f) = R - {3}
Im(f) = [0 , +∞)
Puntos de corte:
• x = 0 ⇒ f(0) = - 2/3 ⇒ Corta al eje Y en el punto (0 , -2/3)
• f(x) = 0 ⇒ x - 2 = 0 ⇒ x = 2 ⇒ Corta el eje X en el punto (2, 0)
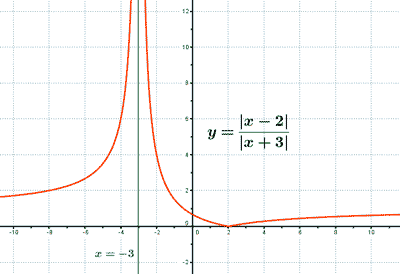
Asíntotas:
Posee una asíntota vertical en x = - 3 (valor que anula al denominador)


 INICIO
INICIO