Ejercicios de interpretación geométrica de la derivada
Líneas rectas

![]()
![]()
![]()
![]()
![]()
Curvas
![]()
![]()
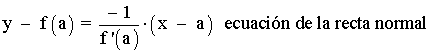
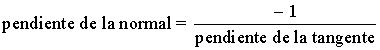
Calcula las ecuaciones de las rectas tangente y normal a la curva f(x) = x2 - 4 en el punto (1, -3) .
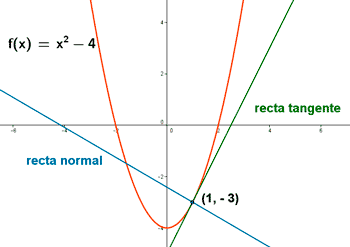
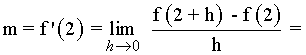
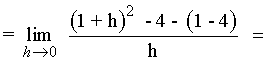
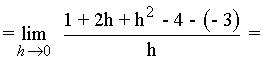
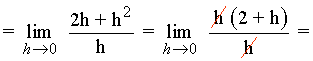
![]()
La ecuación de la recta tangente es:
![]()
![]()
![]()
![]()
Y la ecuación de la recta normal:
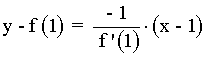
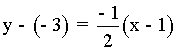
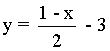
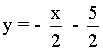
Calcula las ecuaciones de las rectas tangente y normal a la curva f(x) = -6/x en el punto (-2, 3) .
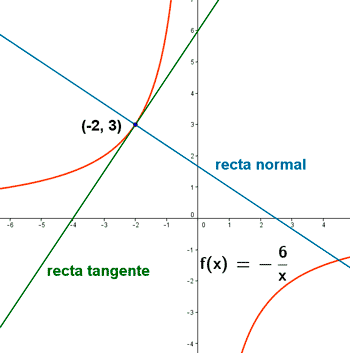
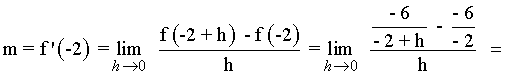
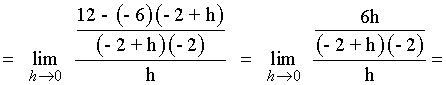
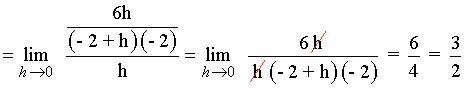
La ecuación de la recta tangente es:
![]()
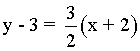
![]()
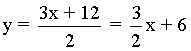
Y la ecuación de la recta normal:
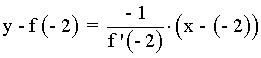
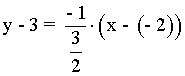
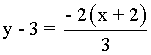
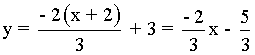
Hallar el ángulo que la tangente a la curva y = 1/(x -1) forma con el eje OX , en el punto de abscisa x = 2 .
Sabemos que: tg α = f '(2)
Calculamos la derivada de la curva:
![]()
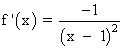
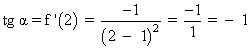
Despejamos el ángulo α aplicando la inversa de la tangente:
tg α = - 1 ⇔ α = 135º
¿Qué ángulo forma la tangente a la curva y = x /(1 + x2) en el origen de coordenadas y el eje OX?
Calculamos la derivada de la curva:
![]()
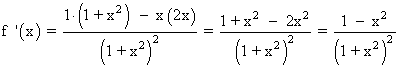
El punto del origen de coordenadas (y = 0) y eje OX (x = 0) es el punto: P(0 , 0)
Por tanto, para calcular el ángulo de la tangente en dicho punto hacemos:
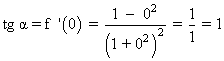
Para saber el ángulo α aplicamos la inversa de la tangente:
tg α = 1 ⇔ α = 45º
Resuelve:
a) ¿En qué puntos la derivada de la función y = x3 + 3x2 - 9x + 5 toma el valor cero?
b) ¿Cómo será la recta tangente a esta curva en dichos puntos?
c) Halla las ecuaciones de dichas tangentes.
a) ¿En qué puntos la derivada de la función y = x3 + 3x2 - 9x + 5 toma el valor cero?
Calculamos primero la derivada de dicha función:
y' = 3x3-1 + 3·2x2-1 - 9 = 3x2 + 6x - 9
Veamos ahora para qué valores de x , la derivada vale cero:
y' = 0 ⇔ 3x2 + 6x - 9 = 0
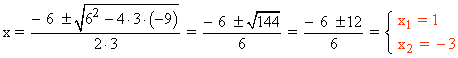
b) ¿Cómo será la recta tangente a esta curva en dichos puntos?
Las rectas tangentes en dichos puntos serán rectas horizontales, ya que sus pendientes son nulas.
c) Halla las ecuaciones de dichas tangentes.
Para x = 1
y - f(1) = f '(1) · (x - 1)
y - 0 = 0 · (x - 1)
y = 0
Para x = - 3
y - f(-3) = f '(-3) · [ x - (-3) ]
y - 32 = 0 · (x + 3)
y = 32
¿Cómo se hallan los puntos de la gráfica de la función en los cuales la tangente es paralela al eje OX? Aplíquese al ejemplo y = x3 - 3x .
La ecuación de la recta del eje OX es: y = 0
Por tango, en la forma pendiente - ordenada en el origen, la pendiente es el coeficiente de la x (y = mx + n) : m = 0
Si la tangente es paralela al eje OX deberá tener su misma pendiente: m = y' = f '(x) = 0
Calculamos los puntos que nos piden:
y = x3 - 3x
m = y' = 3x2 - 3 = 0 ⇔ 3x2 = 3 ⇔ x2 = 1 ⇔ x = ± 1
Si x = 1 ⇒ f(1) = 13 - 3·1 = - 2
Si x = -1 ⇒ f(-1) = (-1)3 - 3·(-1) = 2
Luego los puntos son: A(1 , -2) , B(-1 , 2)
La ecuación de la recta tangente en cada punto es:
y - f(1) = f '(1)(x - 1) ⇔ y + 2 = 0 ⇔ y = - 2
y - f(-1) = f '(-1)(x + 1) ⇔ y - 2 = 0 ⇔ y = 2
¿En qué punto la recta tangente a la gráfica de la función y = x2 + 5x - 6 es paralela a la bisectriz del primer cuadrante? Halla la ecuación de dicha tangente.
La bisectriz del primer cuadrante es la recta y = x .
Por tango, en la forma pendiente - ordenada en el origen, la pendiente es el coeficiente de la x (y = mx + n) : m = 1
Para que la tangente que buscamos sea paralela a la bisectriz, deberá tener su misma pendiente. Por tanto:
m = f '(x) = 2x + 5 ⇔ 1 = 2x + 5 ⇔ 1 - 5 = 2x ⇔ - 4 = 2x ⇔ x = - 2
Calculamos la ordenada:
x = - 2 , f(x) = x2 + 5x - 6 ⇒ f(-2) = (-2)2 + 5·(-2) - 6 = 4 - 10 - 6 = - 12
Por tanto, la recta tangente será paralela a dicha bisectriz en el punto (-2 , -12) .
Hallamos la ecuación de la recta tangente en el punto obtenido:
y - f(-2) = f '(-2)·[x - (-2) ]
y - (-12) = 1 · (x + 2)
y + 12 = x + 2
y = x - 10
Sea la curva dada por la función:
![]()
a) La recta tangente a la gráfica de la curva en el punto P que tiene de abscisa el valor x = 3.
b) El punto de corte entre la tangente hallada en el apartado anterior y la asíntota horizontal de la curva.
a) La recta tangente a la gráfica de la curva en el punto P que tiene de abscisa el valor x = 3.
La ecuación de la recta tangente a una curva en la abscisa x = 3 es de la forma:
y - f(3) = m (x - 3)
Calculamos f(3) y m :
![]()
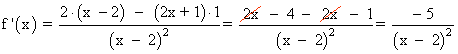
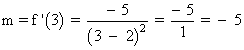
La ecuación de la recta tangente en P es:
y - 7 = (-5)(x - 3)
y - 7 = - 5x + 15
y = - 5x + 22
b) El punto de corte entre la tangente hallada en el apartado anterior y la asíntota horizontal de la curva.
La asíntota horizontal de la curva será aquel valor de x que anule al denominador de la función: x - 2 = 0 ⇔ x = 2
Por tanto, la ecuación de la asíntota horizontal es: y = 2
Queremos hallar el punto de corte entre la tangente y dicha asíntota horizontal, es decir, queremos calcular el punto que verifica ambas ecuaciones de las rectas.
Para ello resolvemos el sistema formado por ambas ecuaciones:
![]()
Luego el punto que buscamos es: P (4 , 2)
Obtenga una ecuación de la recta tangente a la gráfica de la función seno en el punto (π , 0) .
Consideremos pues la función f(x) = sen x .
La ecuación de la recta tangente a f en el punto dado es de la forma:
y - f(π) = f '(π) (x - π)
Calculamos f(π) y f '(π) :
f(π) = sen (π) = 0
f '(x) = cos x
f '(π) = cos (π) = - 1
Luego la ecuación de la recta tangente queda:
y - 0 = (-1)· (x - π) ⇒ y = - x + π
Encontrar la ecuación de la recta tangente a la gráfica de f(x) = 2 cos x + sen 2x en el punto (2π , 1) .
La ecuación de la recta tangente a f en el punto dado es de la forma:
y - f(2π) = f '(2π) (x - 2π)
Calculamos f(2π) y f '(2π) :
f(2π) = 2 cos (2π) + sen (2·2π) = 2 · 1 + 0 = 2
f '(x) = - 2 sen x + 2 cos 2x
f '(2π) = - 2 sen (2π) + 2 cos (2·2π) = - 2 · 0 + 2 · 1 = 2
Luego la ecuación de la recta tangente queda:
y - 2 = 2 (x - 2π) ⇒ y - 2 = 2x - 4π ⇒ y = 2 + 2x - 4π
Hallar las ecuaciones de las tangentes a la elipse en los puntos de abscisa x0 = 1 :
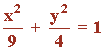
Obtenemos las ordenadas del punto de abscisa x0 = 1 , es decir, calculamos y(1):
![]()
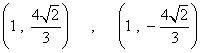
Para hallar la pendiente en dichos puntos, tenemos que derivar implícitamente la ecuación de la elipse:
![]()
Despejamos y' :
![]()
Calculamos y '(1) :
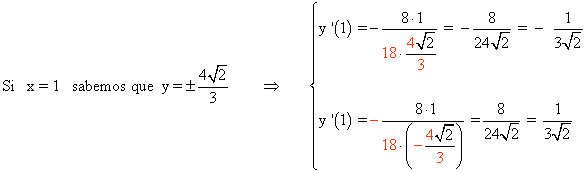
Entonces, las rectas tangentes a la elipse por dichos puntos son:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Halla las ecuaciones de la recta tangente y de la recta normal a la gráfica de la función g(x) = |x2 - 16| en los puntos de abscisa: x = 3 , x = 4
Lo hacemos para el punto x = 3 :
Calculamos f(3) y f '(3) :
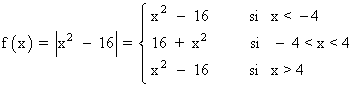
f(3) = | 32 -16| = | - 7 | = 7
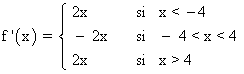
f '(3) = - 2 · 3 = - 6
Luego la ecuación de la recta tangente es:
y - f(3) = f '(3)(x - 3) ⇒ y - 7 = (- 6) (x - 3) ⇒ y - 7 = - 6x + 18 ⇒ y = - 6x + 25
Y la ecuación de la recta normal:
![]()
Lo hacemos para el punto x = 4 :
Calculamos f(4) y f '(4) :
f(4) = | 42 -16| = |0 | = 0
Estudiamos la diferenciabilidad de la función en el punto x = 4 .
La función es continua en todo punto, en particular lo es en x = 4.
Veamos si las derivadas laterales en x = 4 coinciden:
f '(4- ) = - 2 · 4 = - 8
f '(4+) = 2 · 4 = 8
f '(4- ) ≠ f '(4+) ⇒ la función f no es derivable en x = 4
No podemos calcular las rectas tangente y normal a f en dicho punto.


 INICIO
INICIO