Estudio de la derivabilidad de una función
SELECTIVIDAD
Sea f la función definida por:
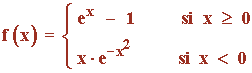
Estudia la derivabilidad de f en x = 0 y, si es posible, calcula la derivada de f en dicho punto.
Para estudiar la derivabilidad de la función en un punto, primero tenemos que ver si es continua en dicho punto.
Para que f sea continua en x = 0 , sus límites laterales tienen que coincidir:
f(0) = e0 - 1 = 1 - 1 = 0
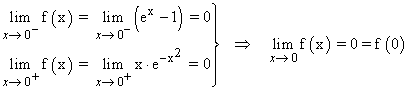
Luego f es continua en x = 0.
Tanto si x < 0 , como si x > 0 , la función f es derivable en dichos intervalos, y su derivada en cada caso es:
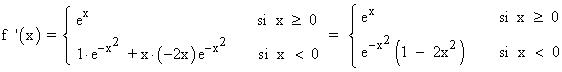
Veamos si f es derivable en x = 0 calculando sus derivadas laterales:
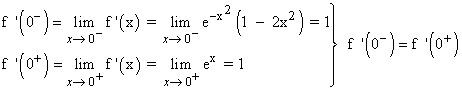
Luego la función f es derivable en x = 0 , y la derivada en dicho punto vale: f '(0) = 1
SELECTIVIDAD
Sea f:(0 , 2) → R la función definida por:
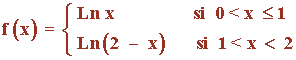
siendo Ln la función logaritmo neperiano.
Estudia la derivabilidad de f en el punto x = 1 .
Para estudiar la derivabilidad de la función en un punto, primero tenemos que ver si es continua en dicho punto.
Para que f sea continua en x = 1 , sus límites laterales tienen que coincidir:
f(1) = Ln 1 = 0
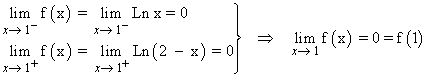
Luego f es continua en x = 1 .
Veamos si es derivable:
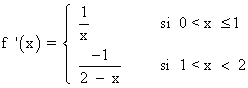
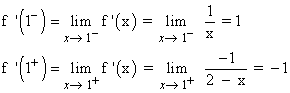
Como f '(1- ) ≠ f '(1+ ) , la función f no es derivable en x = 1 .
SELECTIVIDAD
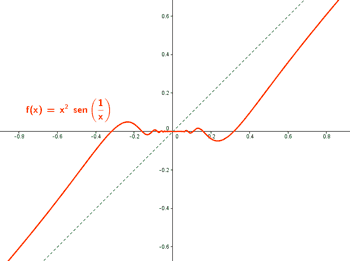
Sea f: R → R la función definida por:
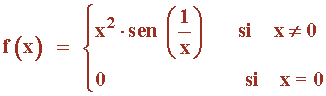
Estudiar la continuidad de f.
Estudiar la derivabilidad de f.
Continuidad:
Para x ≠ 0 la función f es continua por ser el producto de funciones continuas.
Para ver si es continua en x = 0 estudiamos el límite:
f(0) = 0
Observamos que la función sen(1/x) está acotada: -1 ≤ sen (1/x) ≤ 1 ⇔ |sen(1/x)| ≤ 1
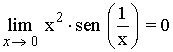
Por tanto:
![]()
La función f es continua en todo R .
Derivabilidad:
Para x ≠ 0 la función f es derivale por ser producto de dos funciones derivables.
Para ver si es derivable en x = 0 estudiamos el límite:
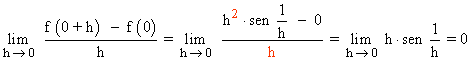
Al igual que antes, se ha tenido en cuenta que la función seno es una función acotada.
Como el límite existe y coincide con f ' (0) = 0, tenemos que la función es derivable en x = 0.
Por tanto, la función es derivable en todo R , siendo:
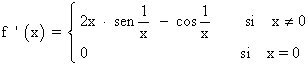
SELECTIVIDAD
Se sabe que la función f : [0 , 5] → R definida por:
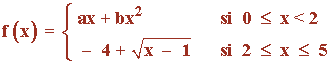
es derivable en el intervalo (0 , 5) .
a) Calcula las constantes a y b .
b) Halla la ecuación de la recta tangente a la gráfica de f en el punto de abscisa x = 2 .
a) Calcula las constantes a y b .
Si la función es derivable en el intervalo (0 , 5), en particular lo es en el punto de abscisa x = 2. Además, como f es derivable en x = 2 , necesariamente es continua en dicho punto.
Imponiendo las condiciones de derivabilidad y continuidad de f en x = 2 obtenemos que:
f continua en x = 2:
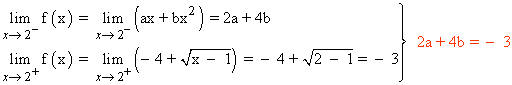
f es derivable en x = 2:
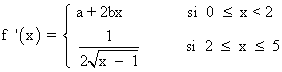
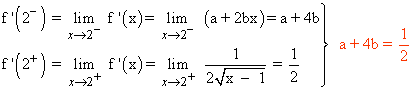
Resolviendo el sistema formado por ambas ecuaciones obtenemos los valores de a y b :
a = - 7/2 , b = 1
b) Halla la ecuación de la recta tangente a la gráfica de f en el punto de abscisa x = 2 .
La ecuación de la recta tangente es:
y - f(2) = f '(2)(x - 2)
Calculamos f(2) y f '(2) :
Si x = 2 ⇒ f(2) = - 3
f '(2) = 1/2
Luego:
y - (-3) = 1/2(x - 2) ⇒ y + 3 = x/2 - 1 ⇒ y = x/2 - 4
Sea la función:
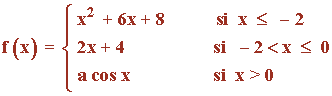
a) Estudia su continuidad en toda la recta real en función de a .
b) Estudia su derivabilidad en toda la recta real en función de a .
c) Para a = 4 , haz un dibujo aproximado de su gráfica.
Si x < 2 , la función f está definida como una función polinómica, por tanto, es continua y además derivable en dicho intervalo.
Si 2 < x < 0 , la función está definida como un polinomio, por lo que también es continua y derivable en éste intervalo.
Si x > 0 , tenemos que f(x) = a cos x, que también es continua y derivable en dicho intervalo.
Veamos ahora la continuidad y derivabilidad de f en los puntos de unión de dichas ramas:
x = - 2 , x = 0
Continuidad:
f(-2) = (-2)2 + 6(-2) + 8 = 4 - 12 + 8 = 0
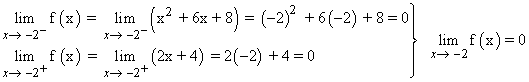
Como los límites laterales coinciden, la función es continua en x = -2 para cualquier valor de a .
f(0) = 2·0 + 4 = 4
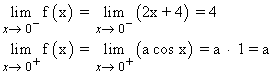
Para que la función sea continua en x = 4 , los límites laterales en dicho punto tienen que coincidir.
Por tanto, si a = 4 la función sí es continua en x = 4 .
Derivabilidad:
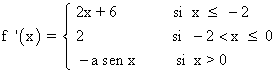
Calculamos las derivadas laterales en cada caso: x = -2 , x = 0
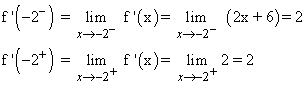
Como f(-2- ) = f(-2+ ) , la función es derivable en x = 2 para cualquier valor de a .
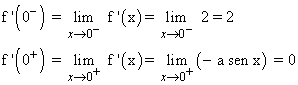
Como f(0- ) ≠ f(0+ ) , la función no es derivable en x = 0 , para ningún valor de a .
Conclusión:
• Si a = 4 , la función es continua en todo R , y si a ≠ 4 , la función es continua en R - {0} .
• La función f es derivable en R - {0} , para todo valor de a .
Hacemos un dibujo aproximado de su gráfica para a = 4 :
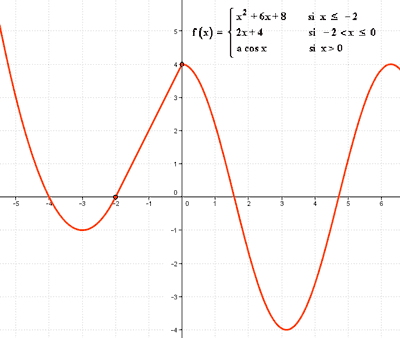
Dada la función:
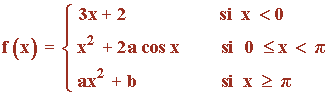
a) Calcular los valores de a y b para que f sea continua para todo valor de x .
b) Estudiar la derivabilidad de f para los valores de a y b obtenidos en el apartado anterior.
Si x < 0 ó si x > π , la función f está definida como funciones polinómicas, por tanto, es continua y además derivable en dichos intervalos.
Si 0 < x < π , la función f está definida como suma de una función polinómica y una trigonométrica (ambas continuas y derivables), por tanto, f es continua y además derivable en dicho intervalo.
Veamos ahora la continuidad y derivabilidad de f en los puntos de unión de dichas ramas:
x = 0 , x = π
Continuidad:
f(0) = 0 + 2a·1 = 2a
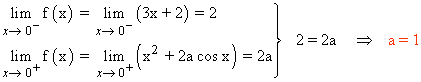
Para que la función sea continua en x = 0 , los límites laterales en dicho punto tienen que coincidir.
f(π) = aπ2 + b
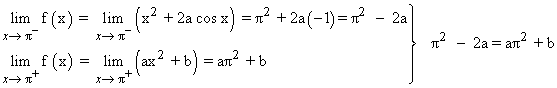
Para que la función sea continua en x = π , los límites laterales en dicho punto tienen que coincidir.
Como a = 1 , podemos obtener el valor de b de la segunda ecuación:
π2 - 2a = aπ2 + b ⇒ π2 - 2 = π2 + b ⇒ b = - 2
Luego si a = 1 y b = - 2 , la función es continua para todo valor de x .
Derivabilidad:
Teniendo en cuenta que a = 1 y b = -2 , tenemos:
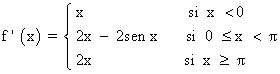
Calculamos las derivadas laterales en cada caso: x = 0 , x = π
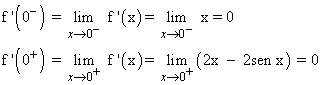
Como f(0- ) = f(0+ ) , la función es derivable en x = 0 .
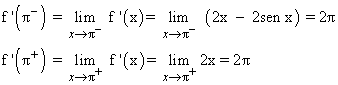
Como f(π- ) = f(π+ ) , la función es derivable en x = π .
Conclusión:
• Si a = 1 y b = - 2 , la función es continua para todo x .
• Si a = 1 y b = - 2 , la función es derivable para todo x .
SELECTIVIDAD
Sea f una función definida por:
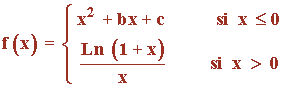
a) Obtener c para que f sea continua en x = 0 .
b) Obenter b para que f sea derivable en x = 0 .
a) Obtener c para que f sea continua en x = 0 .
Para que f sea continua en x = 0 los límites laterales tienen que coincidir con f(0) :
f(0) = 0 + 0 + c = c
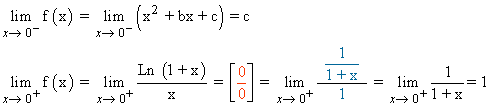
Para resolver la indeterminación 0/0 hemos aplicado la regla del l'Hôpital.
Por tanto: c = 1
b) Obenter b para que f sea derivable en x = 0 .
Para que f sea derivable en x = 0 , las derivadas laterales en dicho punto tienen que coincidir.
Si x ≤ 0 : f(x) = x2 + bx + c ⇒ f '(x) = 2x + b
f '(0- ) = b
Si x > 0 :
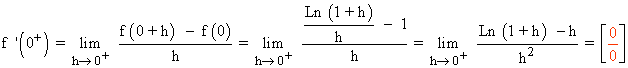
Para resolver la indeterminación aplicamos la regla de l'Hôpital dos veces:
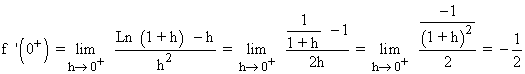
Por tanto, f es derivable en x = 0 si :
f '(0- ) = f(0+ ) ⇔ b = - 1/2
Para calcular la derivada lateral en 0+ hemos aplicado la definición de derivada en un punto, pero tambíen podríamos haber calculado la derivada por la regla correspondiente y depués haber hallado el límite.
Para calcular dicho límite habrá que aplicar dos veces la regla de l'Hôpital.
Conclusión:
Si c = 1 y b = -1/2 la función es continua y derivable en x = 0.
SELECTIVIDAD
Considera la función f: (-∞ , 10) → R definida por:
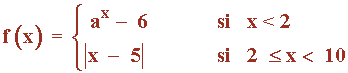
a) Determina el valor de a sabiendo que f es continua (y que a > 0).
b) Esboza la gráfica de f .
c) Estudia la derivabilidad de f .
a) Determina el valor de a sabiendo que f es continua (y que a > 0).
Reescribimos la función:
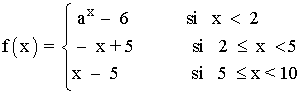
Las funciones que definen f son continuas en todo R , y en particular lo son en sus respectivos intervalos de definición.
Como nos afirman que la función f es continua, en particular lo es en los puntos de unión:
x = 2 , x = 5
En cada caso se tiene que cumplir:
![]()
x = 2
f(2) = - 2 + 5 = 3
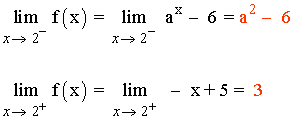
Para que el límite cuando x → 2 exista los límites laterales tienen que coincidir:
![]()
Si a = 3 > 0 se cumple la condición de continuidad:
![]()
x = 5
f(5) = 5 - 5 = 0
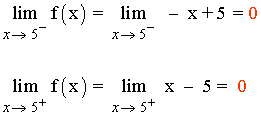
Como los límites laterales coinciden, el límite cuando x → 5 existe y vale:
![]()
Por tanto, para que la función sea continua en (-∞ , 10) tiene que ser a = 3 .
b) Esboza la gráfica de f.
Hallamos los puntos de corte con los ejes:
• Si x = 0 : y = f(0) = 30 - 6 = 1 - 6 = - 5 ⇒ (0 , -5)
• Si y = 0 : 3x - 6 = 0 3x = 6 ⇒ log3 6 = x ⇒ (log3 6 , 0)
- x + 5 = 0 ⇒ x = 5 ⇒ (5 , 0)
x - 5 = 0 ⇒ x = 5 ⇒ (5 , 0)
Como la función es continua en los puntos de unión, podemos hallar dichos puntos:
• x = 2 : f(2) = - 2 + 5 = 3 ⇒ (2 , 3)
• x = 5 : f(5) = 5 - 5 = 0 ⇒ (5 , 0)
La función f no tiene asíntotas verticales. Veamos si tiene horizontales:
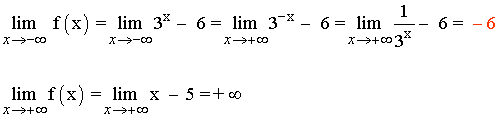
Hay una asíntota horizontal en y = -6.
Como hay asíntota horizontal, no hay oblicua.
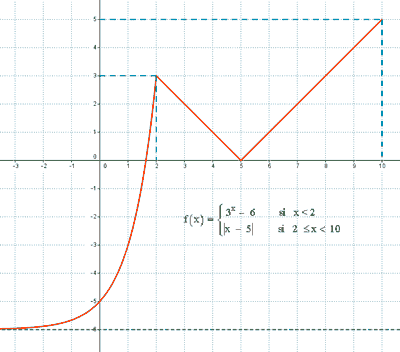
c) Estudia la derivabilidad de f .
La función f es derivable en cada rama, por estar definida por funciones polinómicas y exponenciales.
La derivada de la función en en cada rama, teniendo en cuenta que a = 3, es:
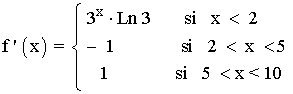
Veamos si es derivable en x = 2 y en x = 5 calculando sus correspondientes derivadas laterales.
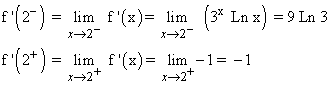
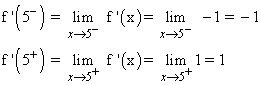
Como las derivadas laterales no coinciden, la función no es derivable en x = 2 , ni tampoco en x = 5.
La función es derivable en: (-∞ , 10] - {2 , 5}
SELECTIVIDAD
Sea f: R → R la función continua definida por:
donde a es un número real.
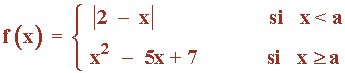
a) Determina a .
b) Halla la función derivada de f .
a) Determina a .
Las funciones que definen a f son funciones continuas en todo R , en particular, en sus respectivos intervalos de definición.
Tenemos que estudiar la continuidad en el punto de unión. Según el valor de a , la función f se define:
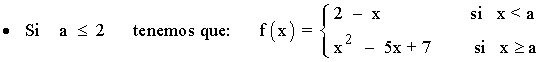
f(a) = a2 - 5a + 7
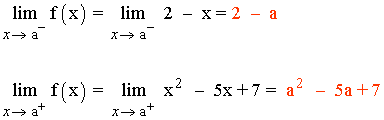
Para que el límite cuando x → a exista los límites laterales tienen que coincidir:
![]()
Por tanto, si a ≤ 2 la función no puede ser continua en a .
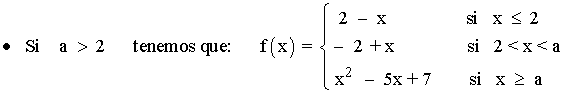
Tenemos que estudiar la continuidad en los puntos: x = 2 , x = a
x = 2
f(2) = 2 - 2 = 0
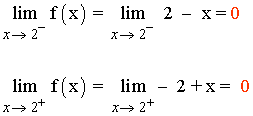
Como los límites laterales coinciden, el límite cuando x → 2 existe y vale:
![]()
Luego la función f es continua en x = 2 .
x = a
f(a) = a2 - 5a + 7
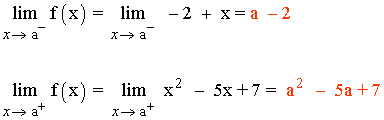
Para que el límite cuando x → a exista los límites laterales tienen que coincidir:
![]()
Si a = 3 los límites laterales coinciden, y por tanto, el límite cuando x → a existe y vale:
![]()
Luego la función f es continua en x = a .
Conclusión:
• Si a ≤ 2 : la función es continua en (-∞ , a) ∪ (a , ∞)
• Si a > 2 : la función es continua en todo R .
b) Halla la función derivada de f .
a ≤ 2 :
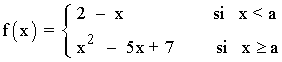
La función es derivable en cada rama por estar definida por funciones polinómicas, y su derivada es:
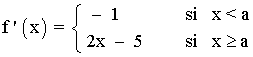
a > 2 :
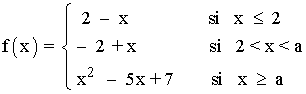
La función es derivable en cada rama por estar definida por funciones polinómicas, y su derivada es:
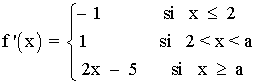
SELECTIVIDAD
a) Determina si la función f(x) = |x| - x es derivable en x = 0 .
b) De entre todos los números reales positivos x , y que suman 15 encuentra aquellos para los que el producto x2y es máximo.
a) Determina si la función f(x) = |x| - x es derivable en x = 0 .
En primer lugar reescribimos la función:
![]()
Las funciones que definen a f son continuas en todo R , por lo que si x < 0 o si x > 0 , la función f es continua. Veamos si f es continua en x = 0 :
f(0) = 0
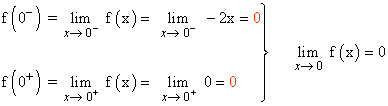
Como el límite cuando x → 0 coincide con f(0) tenemos que la función también es continua en x = 0 . Luego f es continua en todo R .
Las funciones que definen a f son derivables en todo R , por lo que si x < 0 o si x > 0 , la función f es derivable, y :
![]()
Veamos si f es derivable en x = 0:
f ' (0-) = -2 f ' (0+) = 0
Como f ' (0- ) ≠ f ' (0+) la función no es derivable en x = 0 .
b) De entre todos los números reales positivos x , y que suman 15 encuentra aquellos para los que el producto x2y es máximo.
La relación entre las variables x , y es: x + y = 15
Despejamos una de las variables: y = 15 - x
La función a maximizar es : f = x2y
Sustituimos el valor de y en dicha función, quedándonos f en función de x :
f = x2y = x2(15 - x) = 15x2 - x3 ⇒ f(x) = 15x2 - x3
Para encontrar los valores que maximizan a f tenemos que calcular su derivada e igualarla a 0 :
f ' (x) = 15·2x - 3x2 = 30x - 3x2 = 0
Resolvemos la ecuación:
30x - 3x2 = 0 ⇔ 3x(10 - x) = 0 ⇔ 3x = 0 o 10 - x = 0 ⇔ x = 0 o x = 10
Como nos exigen que x sea un número real positivo (x > 0) descartamos el resultado x = 0.
Vamos a comprobar que x = 10 es un máximo:
f ''(x) = 30 - 6x
f ''(10) = 30 - 6·10 = - 30 < 0 ⇒ x = 10 es un máximo de la función f


 INICIO
INICIO