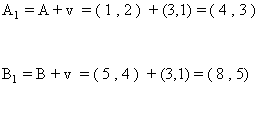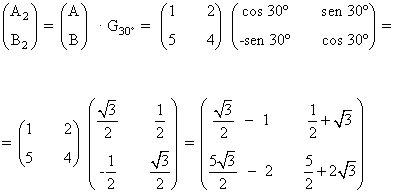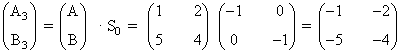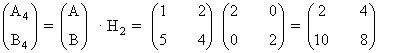Ejercicios y problemas de movimientos en el plano
Traslación con vector guía (a,b)
| Expresión analítica | Expresión matricial | Gráfica |
|---|---|---|
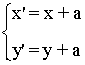 |
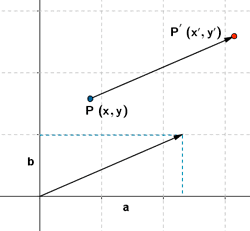 |
Simetría respecto del eje X
| Expresión analítica | Expresión matricial | Gráfica |
|---|---|---|
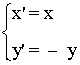 |
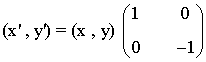 |
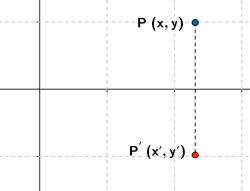 |
Simetría respecto del eje Y
| Expresión analítica | Expresión matricial | Gráfica |
|---|---|---|
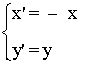 |
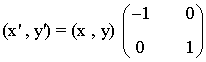 |
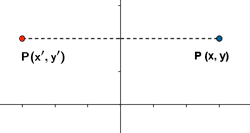 |
Simetría respecto del origen
| Expresión analítica | Expresión matricial | Gráfica |
|---|---|---|
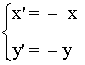 |
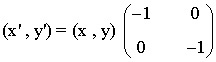 |
 |
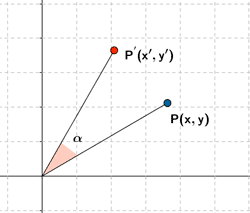
Giro de centro O y ángulo α
| Expresión analítica | Expresión matricial | Gráfica |
|---|---|---|
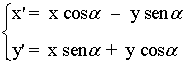 |
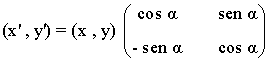 |
 |
Homotecia de centro O y razón k ≠ O
| Expresión analítica | Expresión matricial | Gráfica |
|---|---|---|
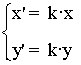 |
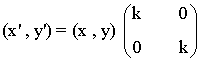 |
 |
1) Dado el punto A de coordenadas ( 4 , -3) halla las coordenadas del punto transformado en los siguientes movimientos:
1. Una traslación con vector guía v = ( 2 , 4 )
2. Un giro de centro el origen y amplitud 60º
3. Una simetría respecto del origen
4. Una homotecia de centro el origen y razón 1.5
2) Dado el segmento de extremos A = ( 1 , 2 ) y B = ( 5 , 4 ) halla el segmento transformado en los siguientes movimientos:
1. Una traslación con vector guía v = ( 3 , 1 ).
2. Un giro de centro el origen y amplitud 30º.
3. Una simetría respecto del origen.
4. Una homotecia de centro el origen y razón 2.
3) El rectángulo de la figura tiene por vértices A = ( 2, 1 ) B = (5 , 1) C = ( 5, 3 ) D = ( 2, 3 ). Estas coordenadas pueden escribirse matricialmente como:
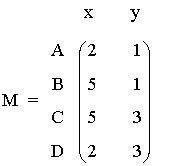
¿Cómo se modifica el rectángulo inicial al aplicarle las transformaciones asociadas a las siguientes matrices?
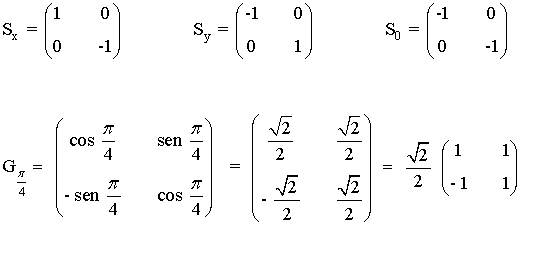
4) Dado el punto A = (-2, 3), hallar su transformado mediante los siguientes movimientos:
1. Una traslación con vector director v = ( 3 , 2 ) primero y un giro con centro el origen y amplitud 180º después.
2. Un giro de centro el origen y amplitud 180º y una traslación con vector guía v = ( 3 , 2 ).
3. ¿Has obtenido los mismos resultados?
5) Un triángulo tiene por vértices a los puntos A=(2,1) B=(6,1) C=(4,4).
¿Cómo se modifica el triángulo inicial al aplicarle las transformaciones dadas por las siguientes matrices?

6) Hallar las matrices asociadas a los siguientes movimientos sucesivos
1. Primero un giro de centro el origen y amplitud 45º y después una simetría respecto del eje Y.
2. Una simetría respecto del eje Y primero y un giro de centro el origen y amplitud 45º después.
¿Qué puede observarse? Responde de forma razonada
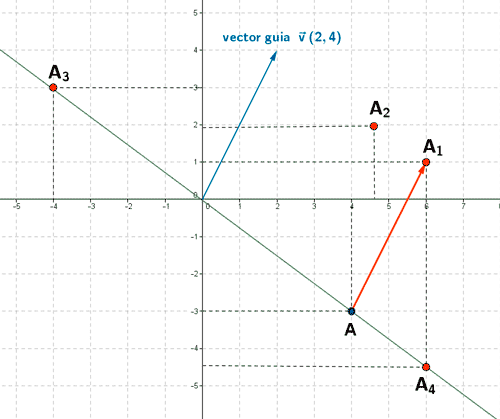
1) Dado el punto A de coordenadas ( 4 , -3) halla las coordenadas del punto transformado en los siguientes movimientos:
1. Una traslación con vector guía v = ( 2 , 4 ).
2. Un giro de centro el origen y amplitud 60º.
3. Una simetría respecto del origen.
4. Una homotecia de centro el origen y razón 1.5 .
- A1 = A + v = (4, -3) + (2 , 4) = (6, 1)
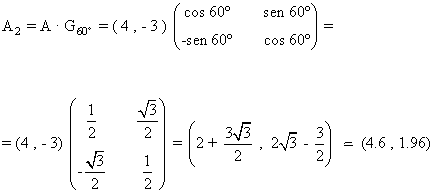
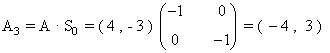
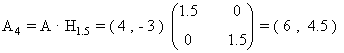
2) Dado el segmento de extremos A = ( 1 , 2 ) y B = ( 5 , 4 ) halla el segmento transformado en los siguientes movimientos:
1. Una traslación con vector guía v = ( 3 , 1 ).
2. Un giro de centro el origen y amplitud 30º.
3. Una simetría respecto del origen.
4. Una homotecia de centro el origen y razón 2.
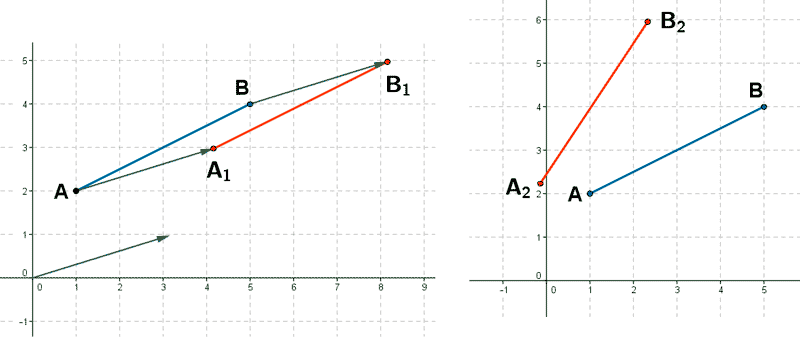
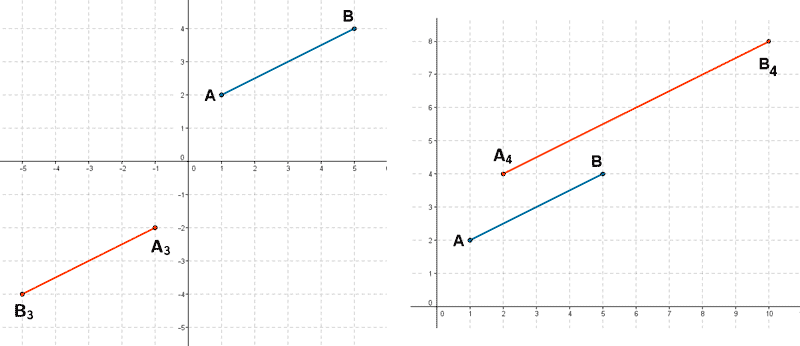
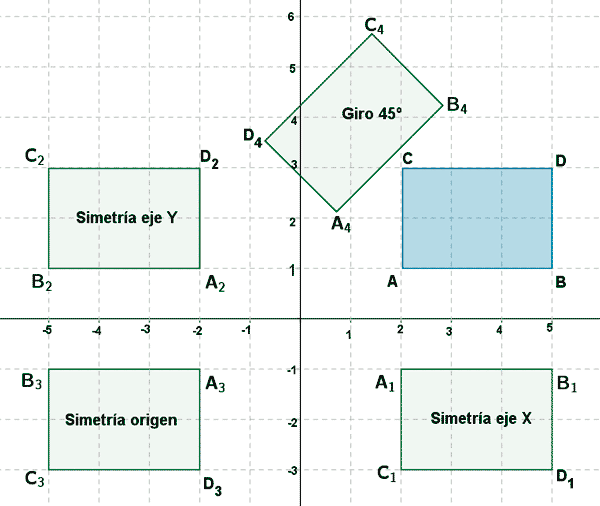
3) El rectángulo de la figura tiene por vértices A = ( 2, 1 ) B = (5 , 1) C = ( 5, 3 ) D = ( 2, 3 ). Estas coordenadas pueden escribirse matricialmente como:
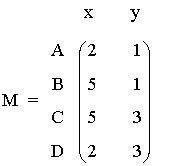
¿Cómo se modifica el rectángulo inicial al aplicarle las transformaciones asociadas a las siguientes matrices?
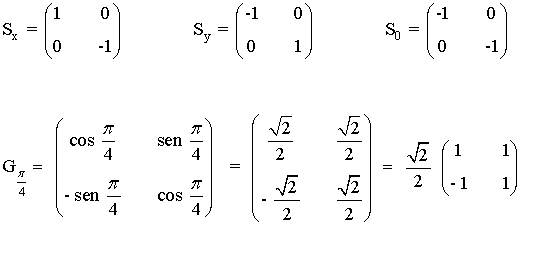
Se modifica como vemos a continuación:
Para la simetría respecto al eje X, que tiene matriz asociada Sx
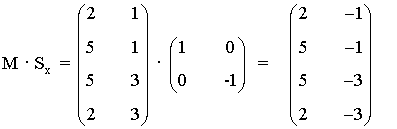
de manera que el rectángulo obtenido al aplicar Sx al rectángulo inicial tiene vértices
A1 = ( 2 , -1 ) , B1 = ( 5 , -1 ) , C1 = ( 5 , -3 ) , D1 = ( 2 , -3 ).
Para la simetría respecto al eje Y, que tiene matriz asociada Sy
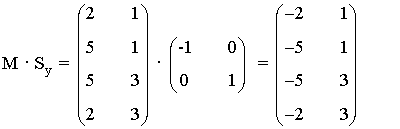
de manera que el rectángulo obtenido al aplicar Sy al rectángulo inicial tiene vértices
A2 = ( -2 , 1 ) , B2 = ( -5 , 1 ) , C2 = ( -5 , 3 ) , D2 = ( -2 , 3 ).
Para la simetría respecto al origen, que tiene matriz asociada S0
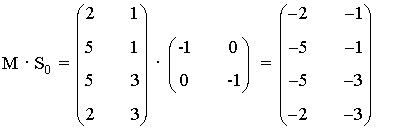
de manera que el rectángulo obtenido al aplicar S0 al rectángulo inicial tiene vértices
A3 = ( -2 , -1 ) , B3 = ( -5 , -1 ) , C3 = ( -5 , -3 ) , D3 = ( -2 , -3 ).
Para la simetría respecto al origen, que tiene matriz asociada S0
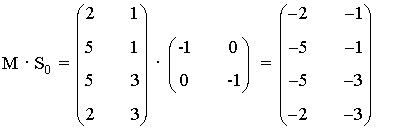
de manera que el rectángulo obtenido al aplicar S0 al rectángulo inicial tiene vértices
A3 = ( -2 , -1 ) , B3 = ( -5 , -1 ) , C3 = ( -5 , -3 ) , D3 = ( -2 , -3 ).
Para el giro de 45 grados que tiene, que tiene matriz asociada Sπ/4
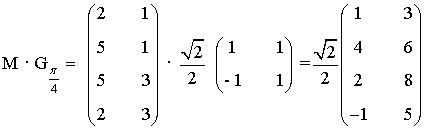
de manera que el rectángulo obtenido al aplicar Sπ/4 al rectángulo inicial tiene vértices
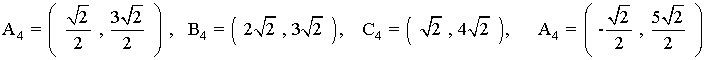
4) Dado el punto A = (-2, 3), hallar su transformado mediante los siguientes movimientos:
1. Una traslación con vector director v = ( 3 , 2 ) primero y un giro con centro el origen y amplitud 180º después.
2. Un giro de centro el origen y amplitud 180º y una traslación con vector guía v = ( 3 , 2 ).
3. ¿Has obtenido los mismos resultados?
1.
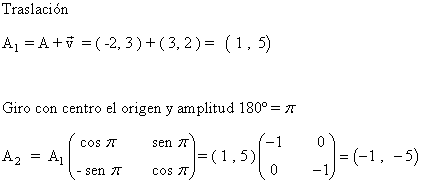
El punto A es enviado por la composición de ambos movimientos al punto A2= ( - 1, -5 )
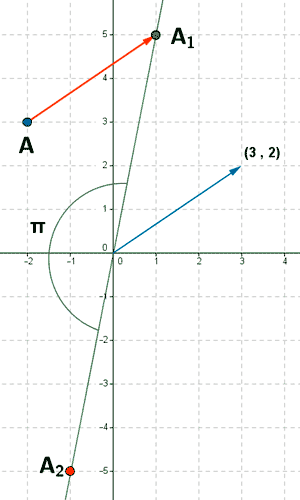
2.
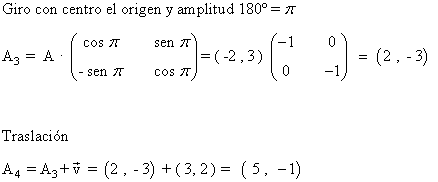
El punto A es enviado por la composición de ambos movimientos al punto A4 = ( 5, -1 )
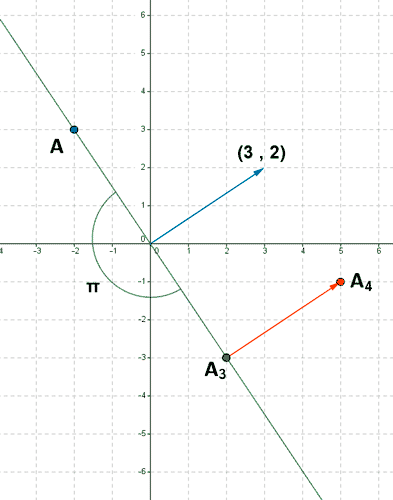
3.
No, ya que los movimientos no son conmutativos en general.
5) Un triángulo tiene por vértices a los puntos A=(2,1) B=(6,1) C=(4,4).
¿Cómo se modifica el triángulo inicial al aplicarle las transformaciones dadas por las siguientes matrices?

Empezamos expresando matricialmente los puntos que forman el triángulo:
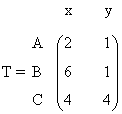
Calculamos cómo se modifica el triángulo inicial por las dos transformaciones. Por la primera,
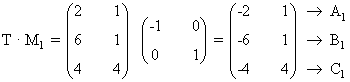
de manera que los vértices del nuevo triángulo son:
A1=( -2 , 1 ) B1=( -6 , 1 ) C1=( -4 , 4 ).
Por la segunda transformación,
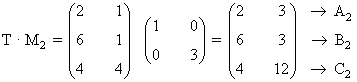
de manera que los vértices del nuevo triángulo son:
A2=( 2 , 3 ) B2=( 6 , 3 ) C2=( 4 , 12 ).
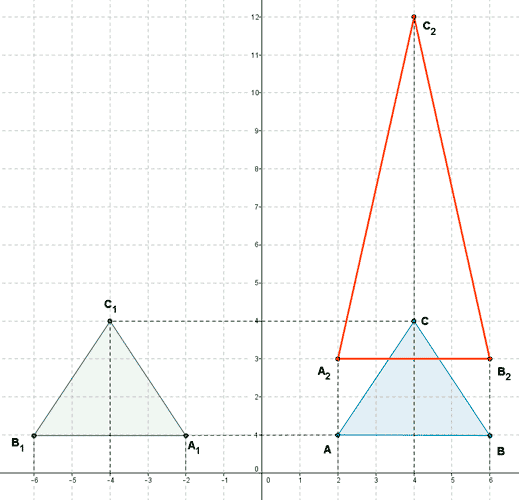
6) Hallar las matrices asociadas a los siguientes movimientos sucesivos
1. Primero un giro de centro el origen y amplitud 45º y después una simetría respecto del eje Y.
2. Una simetría respecto del eje Y primero y un giro de centro el origen y amplitud 45º después.
¿Qué puede observarse? Responde de forma razonada
1.
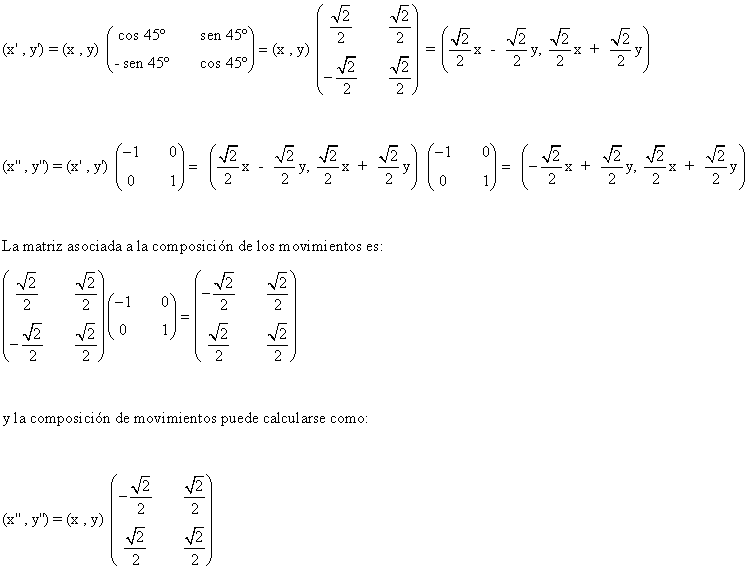
2.
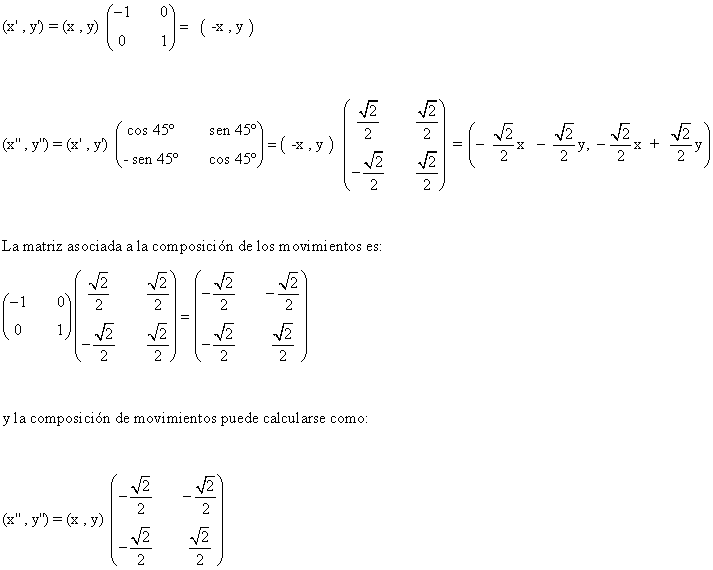
Para acabar, observamos que las composiciones de movimientos no coinciden ya que sus matrices asociadas son distintas. Esta diferencia queda justificada por el hecho de que el producto de matrices no es en general conmutativo.


 INICIO
INICIO