Ejercicios resueltos de inecuaciones con valor absoluto
El conjunto solución de una inecuación con valor absoluto viene dado por las siguientes propiedades:
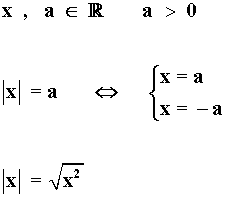
• |x| < a se expresa como:
- a < x < a
• |x| > a se expresa como:
x < - a ó x > a
• |x| ≤ a se expresa como:
- a ≤ x ≤ a
• |x| ≥ a se expresa como:
x ≤ - a ó x ≥ a
Expresión con valor absoluto |
Interpretación Geométrica | Expresión sin valor Absoluto |
|---|---|---|
| |x| = a | La distancia de x al origen es a | x = ± a |
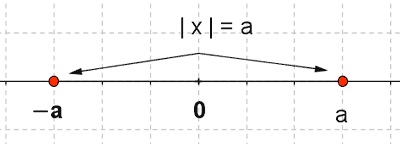 |
||
| |x| < a | La distancia de x al origen es estrictamente menor que a | - a < x < a |
 |
||
| |x| ≤ a | La distancia de x al origen es menor o igual que a | - a ≤ x ≤ a |
 |
||
| |x| > a | La distancia de x al origen es estrictamente mayor que a | x >a ó x < - a |
 |
||
| |x| ≥ a | La distancia de x al origen es mayor o igual que a | x ≥ a ó x ≤ - a |
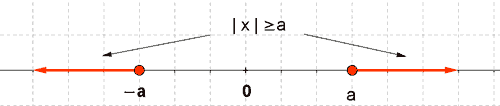 |
||
| 0 < |x| < a | La distancia de x al origen es estrictamente menor que a y estrictamente mayor que 0 | 0 < |x| ⇔ x≠ 0 |x| < a ⇔ - a < x < a Por tanto: 0 < |x| <a ⇔ x≠ 0 y - a < x < a |
 |
||
e < |x| < a |
La distancia de x al origen es estrictamente menor que a y estrictamente mayor que e | e < |x| ⇔ x > e ó x < - e |x| < a ⇔ - a < x < a Por tanto: 0 < |x| < a ⇔ - a < x < -e ó e < x < a |
 |
Expresión con valor absoluto |
Interpretación Geométrica | Expresión sin valor Absoluto |
|---|---|---|
| |x - c| = d | La distancia entre x y c es d | x - c = ± d ⇔ x = d + c ó x = - d +c |
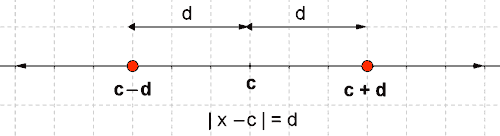 |
||
| |x - c| < d | La distancia entre x y c es estrictamente menor que d | - d < x - c < d ⇔ - d + c < x < d + c |
 |
||
| |x - c| ≤ d | La distancia entre x y c es menor o igual que d | |
 |
- d ≤ x - c ≤ d ⇔ - d + c ≤ x ≤ d + c |
|
| |x - c| > d | La distancia entre x y c es estrictamente mayor que d | x - c > d ó x - c < - d Por tanto: x > c + d ó x < c - d |
 |
||
| |x - c| ≥ d | La distancia entre x y c es mayor o igual que d | x - c ≥ d ó x - c ≤ - d Por tanto: x ≥ c + d ó x ≤ c - d |
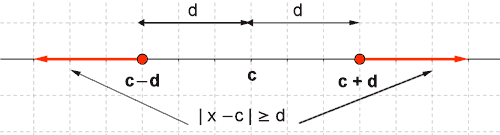 |
||
| 0 < |x - c| < d | La distancia entre x y c es estrictamente menor que d y estrictamente mayor que 0 | 0 < |x - c| ⇔ x - c ≠ 0 ⇔ x ≠c |x - c| < d ⇔ - d + c < x < d + c Por tanto: 0 < |x - c| < d ⇔ x ≠c y - d + c < x < d + c |
 |
||
e < |x- c| < d |
La distancia de x al origen es estrictamente menor que d y estrictamente mayor que e | e < |x - c| ⇔ x > c + e ó x < c - e |x| < d ⇔ - d < x < d Por tanto: 0 < |x| < d ⇔ c - d < x < c - e ó c + e < x < c + d |
 |
2) Resuelve las siguientes inecuaciones:
1) |x| > 4
x < - 4 ó x > 4
x ∈ (-∞ , - 4) ∪ (4 , ∞)
2) |x| < 4
- 4 < x < 4 ⇔ x ∈ (- 4 , 4)
3) |x| ≤ 4
- 4 ≤ x ≤ 4 ⇔ x ∈ [- 4 , 4]
3) Resuelve las siguientes inecuaciones:
1) |x - 3| > 1
x - 3 < - 1 ó x - 3 > 1
x - 3 < - 1 ⇔ x < - 1 + 3 ⇔ x < 2
x - 3 > 1 ⇔ x > 1 + 3 ⇔ x > 4
x ∈ (-∞ , 2) ∪ (4 , ∞)
2) |x - 3| < 1
- 1 < x - 3 < 1
- 1 + 3 < x < 1 + 3
2 < x < 4
x ∈ (2 ,4)
3) |x - 3| ≤ 1
- 1 ≤ x - 3 ≤ 1
- 1 + 3 ≤ x ≤ 1 + 3
2 ≤ x ≤ 4
x ∈ [2 ,4]
4) Resuelve las siguientes inecuaciones:
1) |x - 3| < 2
- 2 < x - 3 < 2
- 2 + 3 < x < 2 + 3
1 < x < 5
x ∈ (1 , 5)
2) |4x + 1| > 0
Siempre se tiene que: |x| ≥ 0 x ∈ R
Como la desigualdad del enunciado es esctricta, el conjunto de soluciones vendrá dado por:
R - { x ∈ R | |4x + 1| = 0 }
|4x + 1| = 0 ⇔ 4x + 1 = 0 ⇔ x = - 1/4
Luego |4x + 1| > 0 ⇔ x ∈ R - { -1/4 }
3) |x - 1| < 5
Los valores reales que verifican dicha expresión son:
|x - 1| < 5 ⇔ - 5 < x - 1 < 5
Por un lado tenemos:
- 5 < x - 1 ⇒ - 5 + 1 < x ⇒ - 4 < x
Por otro:
x - 1 < 5 ⇒ x < 5 + 1 ⇒ x < 6
Por tanto, como - 4 < x < 6 , el conjunto solución es:
S = (-4 , 6)
4) |3x + 1| ≥ 5
Los valores reales que verifican dicha expresión son:
|3x + 1| ≥ 5 ⇔ 3x + 1 ≤ - 5 o 3x + 1 ≥ 5
Por un lado tenemos:
3x + 1 ≤ - 5 ⇒ 3x ≤ - 6 ⇒ x ≤ - 2 ⇒ x ∈ (-∞ , - 2]
Por otro:
3x - 1 ≥ 5 ⇒ 3x ≥ 6 ⇒ x ≥ 2 ⇒ x ∈ [2 , ∞)
Por tanto, el conjunto solución es el intervalo:
S = (-∞ , - 2] ∪ [2 , ∞)
5) Resuelve las siguientes inecuaciones:
1) 3|2 - x| - 15 ≥ 0
3|2 - x| ≥ 15
|2 - x| ≥ 5
2 - x ≤ - 5 ó 2 - x ≥ 5
2 - x ≤ - 5 ⇔ - x ≤ - 5 - 2 ⇔ - x ≤ - 7 x ≥ 7
2 - x ≥ 5 ⇔ - x ≥ 5 - 2 ⇔ - x ≥ 3 x ≤ - 3
La solución será el conjunto de valores de x que cumplan la primera desigualdad ó la segunda.
x ∈ (-∞ , - 3] ∪ [7 , ∞)
2) |x - 1| ≤ 5x - 2
- (5x - 2) ≤ x - 1 ≤ 5x - 2
- 5x + 2 ≤ x - 1 ≤ 5x - 2
a) - 5x + 2 ≤ x - 1 ⇔ 2 + 1 ≤ x + 5x ⇔ 3 ≤ 6x ⇔ 1/2 ≤ x
b) x - 1 ≤ 5x - 2 ⇔ - 1 + 2 ≤ 5x - x ⇔ 1 ≤ 4x ⇔ 1/4 ≤ x
La solución será el conjunto de valores de x que cumplan a) y b), por tanto, es la intersección de los intervalos.
x ∈ [1/2 , ∞) ∩ [1/4 , ∞) = [1/2 , ∞)
6) Resuelve la siguiente inecuación:
4 + |x| ≥ 3x
4 + |x| ≥ 3x
|x| ≥ 3x - 4
x ≤ - (3x - 4) ó x ≥ 3x - 4
x ≤ - (3x - 4) ⇔ x ≤ - 3x + 4 ⇔ 4x ≤ 4 ⇔ x ≤ 1
x ≥ 3x - 4 ⇔ - 2x ≥ - 4 ⇔ 2x ≤ 4 ⇔ x ≤ 2
La solución será el conjunto de valores de x que cumplan la primera desigualdad ó la segunda.
x ∈ (-∞ , 1] ∪ (-∞ , 2] = (-∞ , 2]
7) Resuelve la siguiente inecuación:
|x + 1| ≥ |1 - 2x|
|x + 1| ≥ |1 - 2x|
(|x + 1|)2 ≥ (|1 - 2x|)2
(x + 1)2 ≥ (1 - 2x)2
x2 + 2x + 1 ≥ 1 - 4x + 4x2
0 ≥ 3x2 - 6x
0 ≥ 3x(x - 2)
Tenemos:
3x = 0 ⇔ x = 0
x - 2 = 0 ⇔ x = 2
• (-∞ , 0): x = - 1 ⇒ 3x = - 3 < 0
⇒ x - 2 = - 1 - 2 < 0
• (0, 2): x = 1 ⇒ 3x = 3 > 0
⇒ x - 2 = 1 - 2 < 0
• (2, ∞): x = 3 ⇒ 3x = 9 > 0
⇒ x - 2 = 3 - 2 > 0
También se puede hacer estudiando el signo del numerador y del denominador y después del cociente entre ambos.
| (- ∞ , 0) | (0 , 2) | (2, ∞) | |
|---|---|---|---|
| 3x | - | + | + |
| x - 2 | - | - | + |
| 3x(x - 2) | + | - | + |
El conjunto de soluciones es: [0 , 2]
Incluimos los valores x = 0 y x = 2 , puesto que la desigualdad requiere que el producto sea menor o igual que 0.
8) Resuelve la siguiente inecuación:
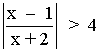
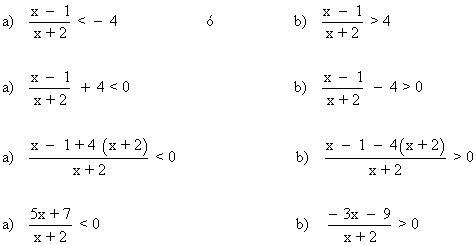
![]()
5x + 7 = 0 ⇔ x = - 7/5
x + 2 = 0 ⇔ x = - 2
• (-∞ , - 2): x = - 3 ⇒ 5x + 7 = - 15 + 7 < 0
⇒ x + 2 = - 3 + 2 < 0
• (-2 , -7/5): x = -3/2 ⇒ 5x + 7 = 5(-3/2) + 7 < 0
⇒ x + 2 = -3/2 + 2 > 0
• (-7/5, ∞): x = 0 ⇒ 5x + 7 = 7 > 0
⇒ x + 2 = 2 > 0
También se puede hacer estudiando el signo del numerador y del denominador y después del cociente entre ambos.
| (- ∞ , - 2) | (-2 , -7/5) | (-7/5, ∞) | |
|---|---|---|---|
| 5x + 7 | - | - | + |
| x + 2 | - | + | + |
| + | - | + |
Para que el cociente sea negativo: x ∈ (-2 , -7/5)
![]()
- 3x - 9 = 0 ⇔ - 3x = 9 ⇔ x = - 3
x + 2 = 0 ⇔ x = - 2
• (-∞ , - 3): x = -4 ⇒ - 3x - 9 = - 3(-4) - 9 > 0
⇒ x + 2 = - 4 + 2< 0
• (- 3 , - 2): x = - 5/2 ⇒ - 3x - 9 = - 3(-5/2) - 9 < 0
⇒ x + 2 = - 5/2 + 2 < 0
• (- 2, ∞): x = 0 ⇒ - 3x - 9 = - 9< 0
⇒ x + 2 = 2 > 0
También se puede hacer estudiando el signo del numerador y del denominador y después del cociente entre ambos.
| (- ∞ , - 3) | (-3 , -2) | (-2, ∞) | |
|---|---|---|---|
| - 3x - 9 | + | - | - |
| x + 2 | - | - | + |
| - | + | - |
Para que el cociente sea positivo: x ∈ (- 3 , - 2)
La solución será el conjunto de valores de x que cumplan la desigualdad a) ó la desigualdad b) , es decir, la unión de sus soluciones.
x ∈ (- 3 , - 2) ∪ (-2 , -7/5)
9) Resuelve la siguiente inecuación: |x2 - 1| < 3
|x2 - 1| < 3
- 3 < x2 - 1 < 3
Resolvemos las dos inecuaciones por separado:
a) x2 - 1 > -3 ⇔ x2 + 2 > 0 ⇒ x > ± √-2
La inecuación no se puede factorizar, así que estudiamos el signo en todo R.
(-∞ , ∞): damos un valor cualquiera en este intervalo, por ejemplo x = 0 ⇒ x2 + 2 = 2 > 0
| (- ∞, ∞) |
|---|
| + |
El conjunto de soluciones es: (-∞ , ∞)
b) x2 - 1 < 3 ⇔ x2 - 4 < 0
x2 - 4 = 0 ⇔ x = ± √4 = ± 2
Factorizamos la inecuación: (x - 2)(x + 2) < 0
Estudiamos el signo en los intervalos: (-∞ , -2) , (-2 , 2) , (2 , ∞)
• (-∞ , -2): x = - 3 ⇒ (x - 2)(x + 2) = (-3 - 2)(-3 + 2) > 0
• (-2 , 2): x = 0 ⇒ (x - 2)(x + 2) = (- 2)(2) < 0
• (2 , ∞): x = 3 ⇒ (x - 2)(x + 2) = (3 - 2)(3 + 2) > 0
| (- ∞, - 2) | (- 2 , 2) | (2 , ∞) |
|---|---|---|
| + | - | + |
El conjunto de soluciones es: (-2 , 2)
La solución será el conjunto de valores de x que cumplan ambas inecuaciones, es decir, será la intersección de los dos conjuntos.
S = (-∞ , ∞) ∩ (-2 , 2) = (-2 , 2)
10) Resuelve la siguiente inecuación: |x2 - 9| ≥ 7
|x2 - 9| ≥ 7
Tenemos dos opciones para resolver la inecuación:
a) x2 - 9 ≤ - 7 ó b) x2 - 9 ≥ 7
Despejando obtenemos que:
a) x2 - 2 ≤ 0 ó b) x2 - 16 ≥ 0
a) x2 - 2 ≤ 0
x2 - 2 = 0 ⇔ x = ± √2
Factorizamos la inecuación: (x - √2)(x + √2) ≤ 0
Estudiamos el signo en los intervalos: (-∞ , -√2) , (-√2 , √2) , (√2 , ∞)
• (-∞ , -√2): x = - 2 ⇒ (x - √2)(x + √2) = (- 2 - √2)(- 2 + √2) > 0
• (-√2 , √2): x = 0 ⇒ (x - √2)(x + √2) = (- √2)(√2) < 0
• (√2 , ∞): x = 2 ⇒ (x - √2)(x + √2) = (2 - √2)(2 + √2) > 0
| (- ∞, - √2) | (- √2 , √2) | (√2 , ∞) |
|---|---|---|
| + | - | + |
El conjunto de soluciones es: [-√2 , √2]
b) x2 - 16 ≥ 0
x2 - 16 = 0 ⇔ x2 = 16 ⇔ x = ± 4
Factorizamos la inecuación: (x - 4)(x + 4) ≥ 0
Estudiamos el signo en los intervalos: (-∞ , - 4) , (- 4 , 4) , (4 , ∞)
• (-∞ , - 4): x = - 5 ⇒ (x - 4)(x + 4) = (- 5 - 4)(- 5 + 4) > 0
• (- 4 , 4): x = 0 ⇒ (x - 4)(x + 4) = (- 4)(4) < 0
• (4, ∞): x = 5 ⇒ (x - 4)(x + 4) = (5 - 4)(5 + 4) > 0
| (- ∞, - 4) | (- 4 , 4) | (4 , ∞) |
|---|---|---|
| + | - | + |
El conjunto de soluciones es: (-∞ , - 4] ∪ [4 , ∞)
La solución será el conjunto de valores de x que cumplan la desigualdad a) ó la desigualdad b) , es decir, la unión de sus soluciones.
x ∈ (-∞ , - 4] ∪ [-√2 , √2] ∪ [4 , ∞)
11) Resuelve la siguiente inecuación: 1 ≤ |x| ≤ 4
Resolvemos las dos inecuaciones por separado:
• |x| ≥ 1 ⇔ x ≤ -1 ó x ≥ 1 ⇔ x ∈ (-∞ , -1] ∪ [1 , +∞)
• |x| ≤ 4 ⇔ - 4 ≤ x ≤ 4 ⇔ x ∈ [-4 , 4]
La solución será el conjunto de valores de x que cumplan ambas desigualdades, es decir, será la intersección de los intervalos.
S = {(-∞ , -1] ∪ [1 , +∞)} ∩ [-4, 4] = [-4 , -1] ∪ [1 , 4]
12) Resuelve la siguiente inecuación:
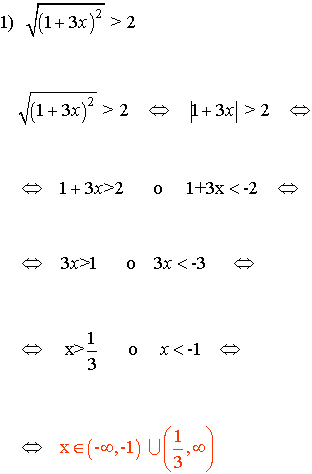


 INICIO
INICIO