Ejercicios resueltos de inecuaciones racionales
Resuelve la siguiente inecuación racional:
![]()
El numerador siempre es positivo, por tanto, para que el cociente sea negativo como indica la desigualdad (< 0) el denominador tiene que ser negativo.
2x - 4 = 0 ⇔ 2x = 4 ⇔ x = 2
Estudiamos el signo del denominador en los intervalos: (-∞ , 2) , (2 , ∞)
• (-∞ , 2): x = 0 ⇒ 2x - 4 = - 4 < 0
• (2 , ∞): x = 3 ⇒ 2x - 4 = 2·3 - 4 = 2 > 0
| (- ∞ , 2) | (2 , ∞) | |
|---|---|---|
| 2x -4 | - | + |
| - | + |
El conjunto de soluciones es: (-∞ , 2)
Resuelve la siguiente inecuación racional:
![]()
El numerador siempre es negativo, por tanto, para que el cociente sea positivo como indica la desigualdad (> 0) el denominador tiene que ser negativo también.
3x - 5 = 0 ⇔ 3x = 5 ⇔ x = 5/3
Estudiamos el signo del denominador en los intervalos: (-∞ , 5/3) , (5/3 , ∞)
• (-∞ , 5/3): x = 0 ⇒ 3x - 5 = - 5 < 0
• (5/3 , ∞): x = 2 ⇒ 3x - 5 = 3·2 - 5 = 1 > 0
| (- ∞ , 5/3) | (5/3 , ∞) | |
|---|---|---|
| - 3 | - | - |
| 3x - 5 | - | + |
| + | - |
El conjunto de soluciones es: (-∞ , 5/3)
Resuelve la siguiente inecuación racional:
![]()
![]()
![]()
Calculamos las raíces del numerador y del denominador:
x - 4 = 0 ⇔ x = 4
x + 2 = 0 ⇔ x = - 2
Estudiamos los signos en los intervalos: (-∞ , -2) , (-2 , 4) , (4 , ∞)
• (-∞ , -2): x = - 3 ⇒ x - 4 = - 3 - 4 = - 7 < 0
⇒ x + 2 = - 3 + 2 = - 1 < 0
• (-2 , 4): x = 0 ⇒ x - 4 = 0 - 4 = - 4 < 0
⇒ x + 2 = 0 + 2 = 2 > 0
• (4 , ∞): x = 5 ⇒ x - 4 = 5 - 4 = 1 > 0
⇒ x + 2 = 5 + 2 = 7 > 0
| (- ∞ , - 2) | (- 2 , 4) | (4 , ∞) | |
|---|---|---|---|
| x - 4 | - | - | + |
| x + 2 | - | + | + |
| + | - | + |
El conjunto de soluciones es: (-∞ , -2) ∪ [4 , ∞)
Incluimos el valor x = 4 , puesto que la desigualdad requiere que el cociente sea mayor o igual que 0.
No incluimos el valor x = - 2 , puesto que el cociente no está definido en - 2.
Resuelve la siguiente inecuación racional:
![]()
![]()
![]()
Calculamos las raíces del numerador y del denominador:
2x = 0 ⇔ x = 0
1 - x = 0 ⇔ x = 1
Estudiamos los signos en los intervalos: (-∞ , 0) , (0 , 1) , (1 , ∞)
• (-∞ , 0): x = - 1 ⇒ 2x = 2·(-1) = - 2 < 0
⇒ 1 - x = 1 - (-1) = 2 > 0
• (0 , 1): x = 1/2 ⇒ 2x = 2·(1/2) = 1 > 0
⇒ 1 - x = 1 - (1/2) = 1/2 > 0
• (1 , ∞): x = 2 ⇒ 2x = 2·2 = 4 > 0
⇒ 1 - x = 1 - 2 = - 1 < 0
| (- ∞ , 0) | (0 , 1) | (1 , ∞) | |
|---|---|---|---|
| 2x | - | + | + |
| 1 - x | + | + | - |
| - | + | - |
El conjunto de soluciones es: [0 , 1)
Incluimos el valor x = 0 , puesto que la desigualdad requiere que el cociente sea mayor o igual que 0.
No incluimos el valor x = 1 , pues el cociente no está definido en 1.
Resuelve la siguiente inecuación racional:
![]()
![]()
![]()
Calculamos las raíces del numerador y del denominador:
x = 0
- x2 - 40x + 4500 = 0
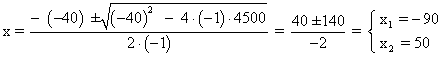
Obtenidas las raíces, podemos factorizar la ecuación de segundo grado:
- x2 - 40x + 4500 = (-1)(x + 90)(x - 50) = (x + 90)(50 - x) = 0
Estudiamos los signos en los intervalos: (-∞ , - 90) , (- 90 , 0) , (0 , 50) , (50 , ∞)
• (-∞ , -90): x = - 100 ⇒ (x + 90)(50 - x) = (-100 + 90)(50 - (-100)) = (-10)(150) = - 1500 < 0
⇒ x = - 100 < 0
• (-90 , 0): x = -10 ⇒ (x + 90)(50 - x) = ((-10) + 90)(50 - (-10)) = (80)(60) = 4800 > 0
⇒ x = - 10 < 0
• (0 , 50): x = 10 ⇒ (x + 90)(50 - x) = (10 + 90)(50 - 10) = (100)(40) = 4000 > 0
⇒ x = 10 > 0
• (50 , ∞): x = 60 ⇒ (x + 90)(50 - x) = (60 + 90)(50 - 60) = (150)(-10) = - 1500 < 0
⇒ x = 60 > 0
| (-∞ , - 90) | (- 90 , 0) | (0 , 50) | (50 , ∞) | |
|---|---|---|---|---|
| - x2 - 40x + 4500 | - | + | + | - |
| x | - | - | + | + |
| + | - | + | - |
El conjunto de soluciones es: (-90 , 0) ∪ (50 , ∞)
Resuelve la siguiente inecuación racional:
![]()
![]()
![]()
Aplicamos el m.c.m. de ambos denominadores: m.c.m.((x-1), (x+1)) = (x - 1)(x + 1)
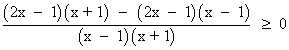
![]()
![]()
Calculamos las raíces del numerador y del denominador:
4x - 2 = 0 ⇔ 4x = 2 ⇔ x = 1/2
(x - 1)(x + 1) = 0 ⇔ x - 1 = 0 o x + 1 = 0 ⇔ x = 1 o x = - 1
Estudiamos los signos en los intervalos: (-∞ , - 1) , (- 1 , 1/2) , (1/2 , 1) , (1 , ∞)
• (-∞ , - 1): x = - 2 ⇒ 4x - 2 = - 10 < 0
⇒ (x - 1)(x + 1) = ((-2) - 1)((-2) + 1) = 3 > 0
• (-1 , 1/2): x = 0 ⇒ 4x - 2 = - 2 < 0
⇒ (x - 1)(x + 1) = - 1 < 0
• (1/2 , 1): x = 3/4 ⇒ 4x - 2 = 4(3/4) - 2 = 3 - 2 = 1 > 0
⇒ (x - 1)(x + 1) = (3/4 - 1)(3/4 + 1) = (-1/4)(7/4) = -7/16 < 0
• (1 , ∞): x = 3 ⇒ 4x - 2 = 4·3 - 2 = 10 > 0
⇒ (x - 1)(x + 1) = (3 - 1)(3 + 1) = 8 > 0
| (-∞ , - 1) | (-1 , 1/2) | (1/2 , 1) | (1 , ∞) | |
|---|---|---|---|---|
| 4x - 2 | - | - | + | + |
| (x - 1)(x + 1) | + | - | - | + |
| - | + | - | + |
El conjunto de soluciones es: (-1 , 1/2] ∪ (1 , ∞)
Incluimos el valor x = 1/2 , puesto que la desigualdad requiere que el cociente sea mayor o igual que 0.
No incluimos los valores x = ±1 , pues el cociente no está definido en ±1.
Resuelve la siguiente inecuación racional:
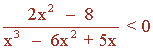
2x2 - 8 = 0 ⇔ x2 = 4 ⇔ x = 2 , x = - 2
x3 - 6x2 + 5x = 0 ⇔ x(x2 - 6x + 5) = 0 ⇔ x = 0 o x2 - 6x + 5 = 0
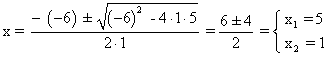
Factorizamos numerador y denominador:

Estudiamos el signo en los intervalos: (-∞ , -2) , (-2 , 0) , (0 , 1) , (1 , 2) , (2 , 5) , (5 , ∞)
• (-∞ , - 2): x = - 3 ⇒ 2(x - 2)(x + 2) = 2(- 3 - 2)(- 3 + 2) > 0
⇒ x(x - 1)(x - 5) = (-3)(- 3 - 1)(- 3 - 5) = (-3)(-4)(-8) < 0
• (-2 , 0): x = - 1 ⇒ 2(x - 2)(x + 2) = 2(- 1 - 2)(- 1 + 2) < 0
⇒ x(x - 1)(x - 5) = (-1)(- 1 - 1)(- 1 - 5) = (-1)(-2)(-6) < 0
• (0 , 1): x = 1/2 ⇒ 2(x - 2)(x + 2) = 2(1/2 - 2)(1/2 + 2) < 0
⇒ x(x - 1)(x - 5) = (1/2)(1/2 - 1)(1/2 - 5) > 0
• (1 , 2): x = 3/2 ⇒ 2(x - 2)(x + 2) = 2(3/2 - 2)(3/2 + 2) < 0
⇒ x(x - 1)(x - 5) = (3/2)(3/2 - 1)(3/2 - 5) < 0
• (2 , 5): x = 3 ⇒ 2(x - 2)(x + 2) = 2(3 - 2)(3 + 2) > 0
⇒ x(x - 1)(x - 5) = (3)(3 - 1)(3 - 5) < 0
• (5 , ∞): x = 6 ⇒ 2(x - 2)(x + 2) = 2(6 - 2)(6 + 2) > 0
⇒ x(x - 1)(x - 5) = (6)(6 - 1)(6 - 5) > 0
| (-∞ , -2) | (-2 , 0) | (0 , 1) | (1 , 2) | (2 , 5) | (5 , ∞) | |
|---|---|---|---|---|---|---|
| 2(x - 2)(x + 2) | + | - | - | - | + | + |
| x(x - 1)(x - 5) | - | - | + | - | - | + |
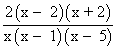 |
- | + | - | + | - | + |
El conjunto de soluciones es: (-∞ , - 2) ∪ (0 , 1) ∪ (2 , 5)


 INICIO
INICIO