Logaritmos
Dados dos números reales positivos a y N (a≠1), el logaritmo en base a de N es el exponente al que hay que elevar la base a para que el resultado sea N
![]()
Por tanto el logaritmo de un número es el exponente al que hay que elevar la base para obtener dicho número.
De la definición se deducen las siguientes igualdades:

Ejemplos:

![]()
![]()
![]()
Logaritmo decimal o de Briggs
Llamamos logaritmo decimal al logaritmo en base 10, y se designa: log
![]()
Ejemplos:

Logaritmo neperiano
Llamamos logarimo neperiano al logaritmo cuya base es el número e, y se designa: Ln
![]()
Ejemplos:

Propiedades de los logaritmos
1. El logaritmo de la base es siempre 1:

2. En cualquier base, el logaritmo de 1 es siempre 0:

3. En cualquier base, tenemos la siguiente relación:
![]()
4. El logaritmo de un producto es igual a la suma de los logaritmos de los factores:

5. El logaritmo de un cociente es igual al logaritmo del numerador menos el del denominador:

6. El logaritmo de una potencia es igual al exponente por el logaritmo de la base de la potencia:

7. El logaritmo de una raíz es igual al logaritmo del radicando dividido por el índice:

8. Cambio de base:
El logaritmo en base a de un número N se puede obtener a partir de logaritmos en otra base b.

o bien, a partir de logaritmos neperianos:
![]()

Cálculo de logaritmos no decimales.
Los logaritmos en base a de un número N es igual al cociente del logaritmo decimal de N entre el logaritmo decimal de a
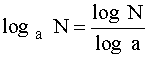
Ejemplo :
Utiliza la calculadora para hallar estos logaritmos con una aproximación a la diezmilésimas :
a) log 2 7 b) log 3 12
c) log 1 / 5 21 d) log 2 / 3 4
Ya que en en la calculadora sólo es posible calcular logaritmos decimales y logaritmos neperiano, convertiremos los logaritmos no decimales en logaritmos decimales.
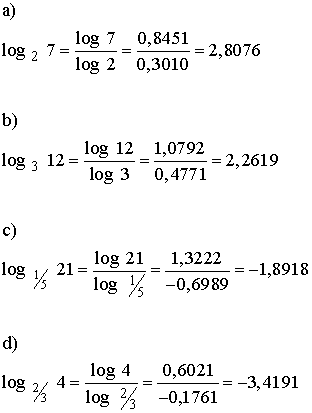


 INICIO
INICIO
