INICIOParámetros estadísticos I : Medidas de centralización.
Media aritmética.
La media aritmética de una serie de datos se obtiene sumando todos los datos y dividiendo entre el número total de ellos. Se representa por 
Para calcular la media aritmética de un conjunto de datos cuyos valores se repiten, podemos utilizar la frecuencia absoluta de cada valor de la variable :
Moda.
La moda ( Mo ) de una serie de datos es el valor de la variable que más se repite, es decir, aquella variable que tiene mayor frecuencia absoluta.
Mediana.
La mediana ( Me ) de una serie de datos se corresponde con el valor que ocupa la posición central de dichos datos ordenados.
Para conocer el valor central, dividimos el número total de datos N entre dos y aquel valor estadístico cuya frecuencia absoluta acumulada sea mayor que el resultado de dicha división.
Ejemplo 1 :
Las notas de matemáticas de los alumnos de una clase son las siguientes :
3, 3, 7, 6, 8, 7, 6, 7, 5, 5, 4, 5, 4, 6, 4,
5, 7, 8, 5, 4, 5, 6, 7, 9, 6, 10, 3, 2, 6, 6
Obtén la tabla de frecuencias, la media aritmética, la mediana y la moda.
| Variable estadística xi |
Frecuencia absoluta fi |
Frecuencia relativa hi |
Frecuencia absoluta acumulada Fi |
Frecuencia relativa acumulada Hi |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 |
| 2 | 1 | 0,033 | 1 | 0,033 |
| 3 | 3 | 0,1 | 4 | 0,133 |
| 4 | 4 | 0,133 | 8 | 0,266 |
| 5 | 6 | 0,2 | 14 | 0,466 |
| 6 | 7 | 0,234 | 21 | 0,7 |
| 7 | 5 | 0,167 | 26 | 0,867 |
| 8 | 2 | 0,067 | 28 | 0,934 |
| 9 | 1 | 0,033 | 29 | 0,967 |
| 10 | 1 | 0,033 | 30 | 1 |
| Sumatorio | N = 30 | 1 |
Media aritmética :
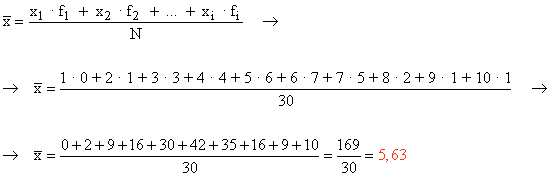
Moda :
La moda es el valor estadístico que más se repite, es decir, con l mayor frecuencia estadística. Luego la moda es : Mo = 6
Mediana :
→ El primer valor estadístico vuya frecuencia absoluta acumulada es mayor a 15 es 6, por lo que la mediana es : Me = 6
