Teorema de Bolzano
Si una función es continua en un intervalo cerrado [a, b] y signo f(a) ≠ signo f(b) , entonces existe un c ∈ [a, b] tal que f(c) = 0 .
Si una función es continua en un intervalo cerrado y en su extremo toma valores de distinto signo, entonces corta al eje X en ese intervalo.
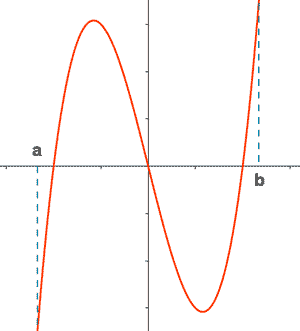
Aplicación del Teorema de Bolzano
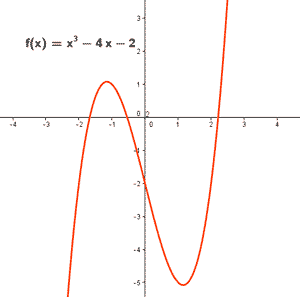
Probar que la ecuación x3 - 4x - 2 = 0 tiene alguna raíz real, aproximando su valor hasta las décimas.
Consideramos la función f(x) = x3 - 4x - 2 la cual es continua por ser polinómica.
Tanteando, tenemos que f(2) = - 2 y f(3) = 13
Es decir, tenemos una función continua en el intervalo [2, 3] donde signo de f(2) ≠ signo de f(3) .
Por lo tanto, por el Teorema de Bolzano, existe un c ∈ [2, 3] tal que f(c) = 0 .
Para aproximar la solución a la décima seguimos tanteando: f(2,2) = - 0,152 y f(2,3) = 0,967
Tememos una función cotinua en el intervalo [2,2, 2,3] donde signo de f(2,2) ≠ signo de f(2,3) .
Es decir, existe un c ∈ [2,2, 2,3] tal que f(c) = 0 .


 INICIO
INICIO

