Límites y continuidad
Límites que conviene conocer
No existen:
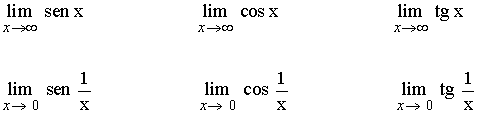
Infinitos:
![]()
Finitos:
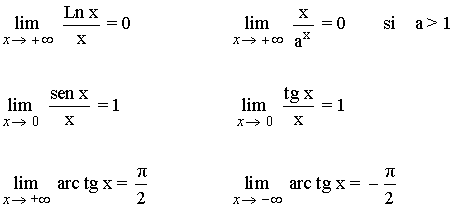
SELECTIVIDAD
Calcula
![]()
cuando:
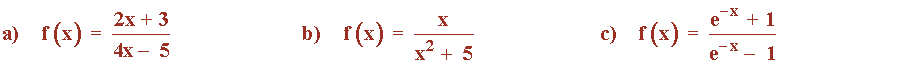
![]()
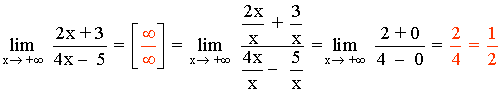
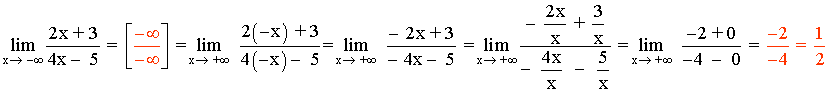
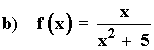
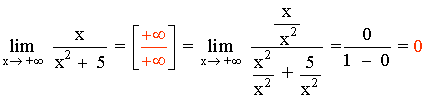
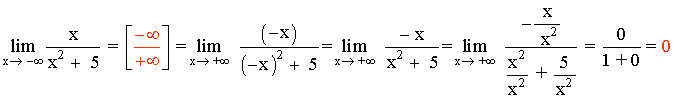
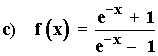
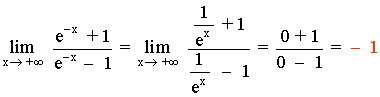
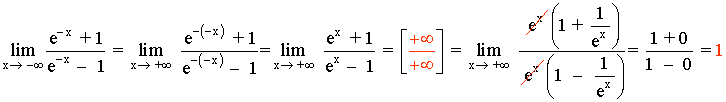
SELECTIVIDAD
Calcular:
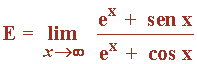
Como hay una expresión exponencial, diferenciaremos los casos + ∞ y - ∞ .
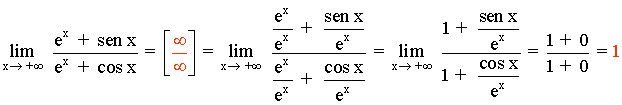
Para resolver los límites:
![]()
Tenemos que tener en cuenta de que se tratan de cocientes entre una función acotada y otra que tiende a infinito.
![]()
Por lo que ambos límites valen 0 .
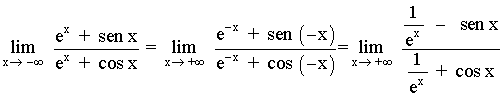
La función seno es una función impar, por tanto: sen(-x) = - sen x
La función coseno es una función par, por tanto: cos(-x) = cos x
Por otro lado, tenemos que:
![]()
Por tanto, calcular el límite anterior es análogo a calcular el siguiente:
![]()
Este límite no existe, ya que cuando x → +∞ la función tangente no tiende a un único valor de R , sino que se mueve en el intervalo (-infin; , +∞).
Si
calcula su límite en los puntos 7 , -3 , 1 y 0 .
![]()
![]()
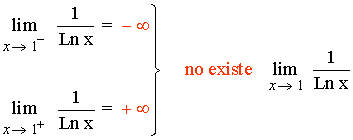
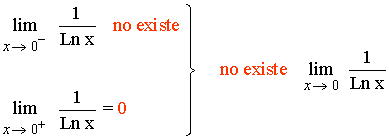
Hallar el intervalo o intervalos donde cada función es continua:
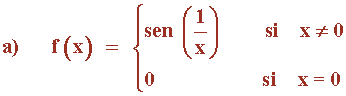
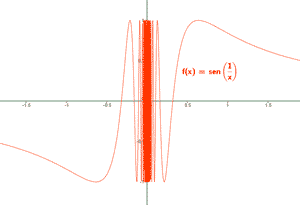
La función y = 1/x es continua excepto en x = 0 y la función seno es continua para todos los valores reales de x .
Por tanto y = sen (1/x) es continua en todos los valores reales excepto en x = 0 .
Cuando f(x) = sen (1/x) se aproxima a 0 f(x) oscila entre - 1 y 1 , por consiguiente el límite no existe.
Por tanto f(x) es continua en los intervalos (-∞, 0) ∪ (0, +∞) .
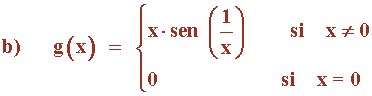
Aplicando el teorema del encaje:
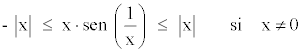
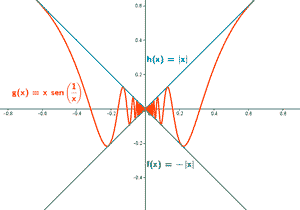
Además, tenemos que:
![]()
Por tanto, la función g(x) es continua en toda la recta real.
SELECTIVIDAD
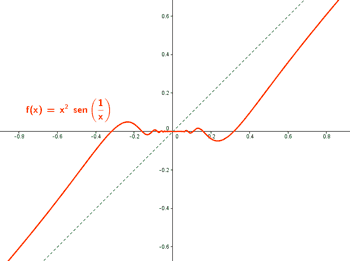
Sea f: R → R la función definida por:
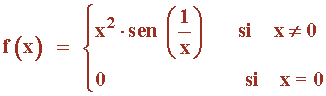
Estudiar la continuidad de f.
Para x ≠ 0 la función f es continua por ser el producto de funciones continuas.
Para ver si es continua en x = 0 estudiamos el límite:
f(0) = 0
Observamos que la función sen(1/x) está acotada: -1 ≤ sen (1/x) ≤ 1 ⇔ |sen(1/x)| ≤ 1
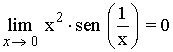
Por tanto:
![]()
La función f es continua en todo R .
SELECTIVIDAD
Estudia la continuidad en el intervalo [0 , 4] de la siguiente función:
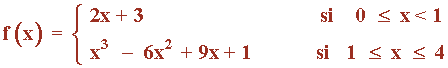
Las funciones que definen a f son funciones polinómicas, por lo que son continuas en todo R , en particular, lo son en (0 , 1) y (1 , 4) respectivamente.
Por tanto, la función f es continua en los intervalos: (0 , 1) ∪ (1 , 4)
Estudiamos la continuidad en el punto de unión: x = 1
f(1) = 13 - 6·12 + 9·1 + 1 = 5
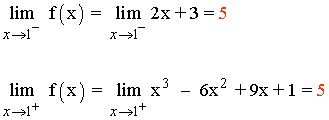
Como los límites laterales coinciden, el límie cuando x → 1 existe y vale:
![]()
Se cumple la condición de continuidad en un punto:
![]()
Luego la función es continua también en 1, y por tanto, es continua en todo el intervalo: (0 , 4)


 INICIO
INICIO