Cáculo de límites relacionados con el número e . Indeterminación 1∞
Hallar el siguiente límite:
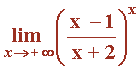
1. Determinamos si el límite es una indeterminación del tipo 1∞:
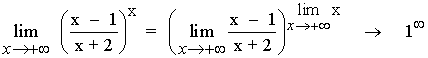
2. Sumamos y restamos 1 dentro del paréntesis, y después, operamos dejando el término +1 despejado:
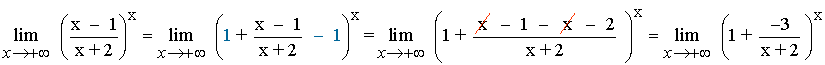
3. Hacemos el inverso del inverso de la fracción que nos ha quedado, que es lo mismo que pasar el numerador de la fracción como denominador de (x+2):
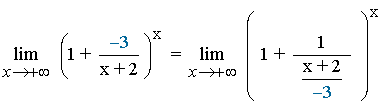
Si aplicamos el inverso del inverso de la fracción resultaría:
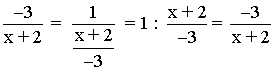
4. Multiplicamos el exponente por el denominador hallado y por su inverso
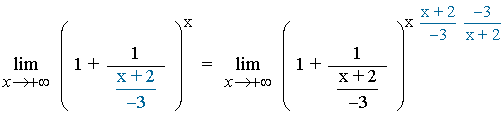
5. Nos quedamos con la parte del exponente que es igual al denominador de la fracción:
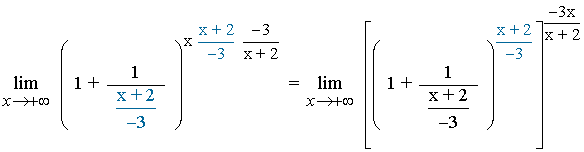
6. Se resuelve el límite aplicando la propiedad de los límites, por la cual tendremos que calcular el límite de la base y el límite del exponente:
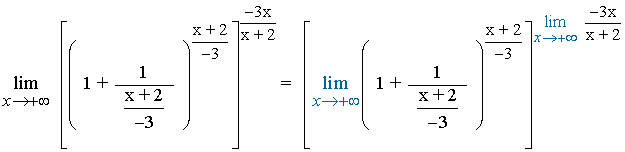
7. Calculamos los límites por separado:
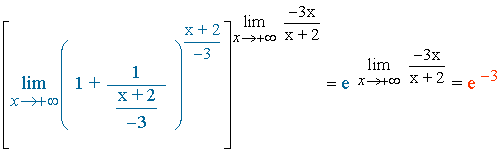
Hallar el siguiente límite:
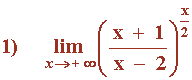
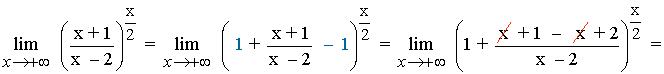
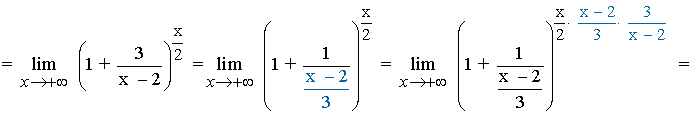
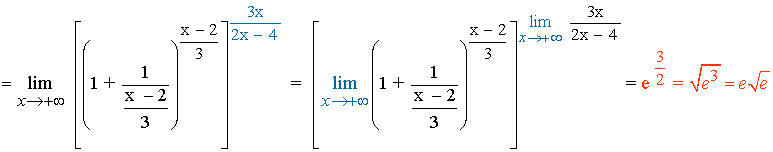
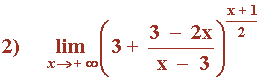
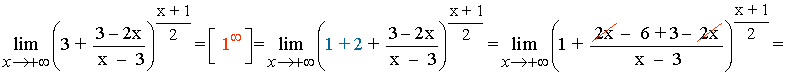
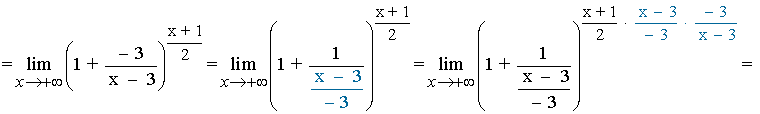
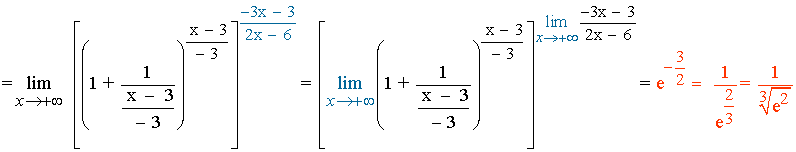
Las indeterminaciones del tipo 1∞ también se pueden resolver con el siguiente método práctico cuando x → ∞ :
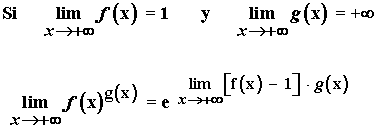
Hallar los siguientes límites:
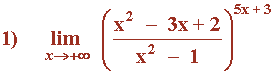
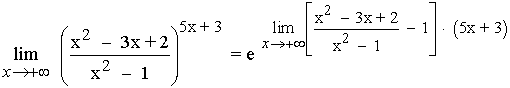
Calculamos el límite del exponente por separado:
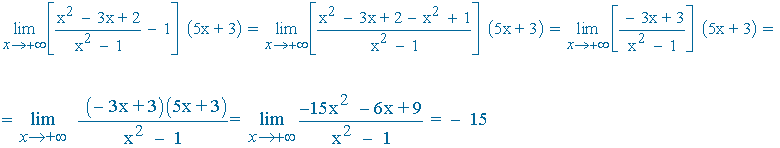
Aplicamos el resultado:
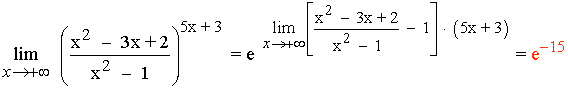
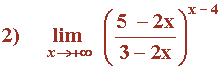
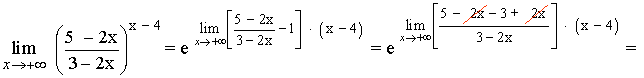
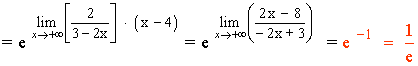
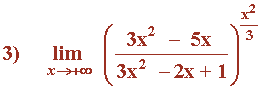
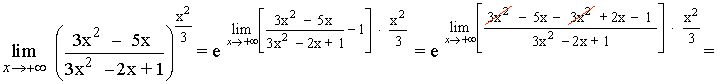
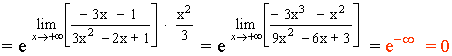
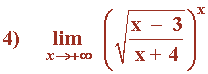
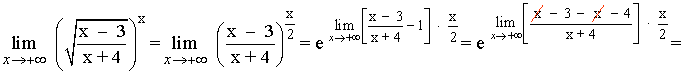
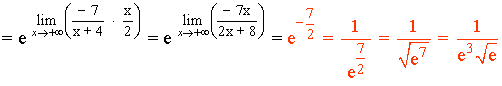
Las indeterminaciones del tipo 1∞ también se pueden resolver con el siguiente método práctico cuando x → a :
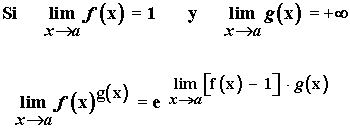
Hallar los siguientes límites:
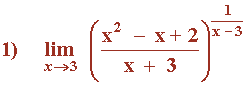
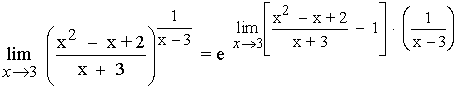
Calculamos el límite del exponente por separado:
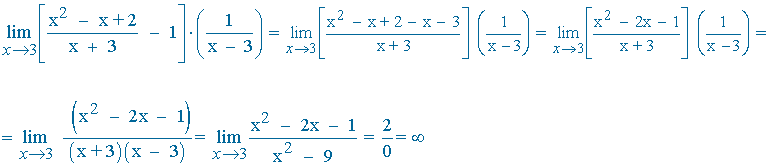
Aplicamos el resultado:
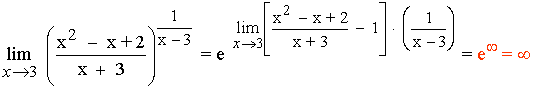
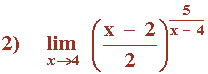
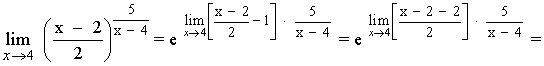
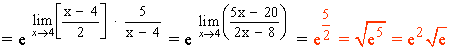
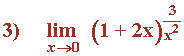
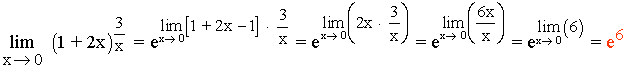
Calcula la incógnita a para que se cumpla que:
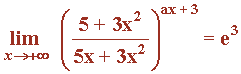
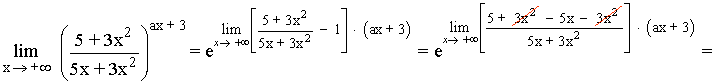
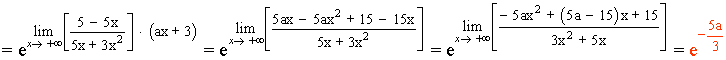
Como el límite tiene que dar e3 , lo igualamos con nuestro resultado:



 INICIO
INICIO