Las funciones racionales del tipo:
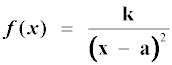
son funciones racionales cuyo denominador es un polinomio de segundo grado y su numerador es un número real.
Las características generales de este tipo de funciones racionales son:
1) El dominio está formado por todos los valores reales que no anulan el denominador:
Dom(f) = R - {a}
2) El recorrido depende del signo de la constante k :
• Si k > 0 ⇒ Im(f) = (0 , ∞)
• Si k < 0 ⇒ Im(f) = (-∞ , 0)
3) No cortan al eje X (abscisas), y cortan al eje Y (ordenadas) en el punto:
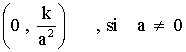
4) Son discontinuas en el punto de abscisa: x = a .
5) La acotación depende del signo de la constante k :
• Si k > 0 : están acotadas inferiormente por y = 0 .
• Si k < 0 : están acotadas superiormente por y = 0 .
En cualquier caso, la función no está acotada, pues no está acotada, a la vez, superior e inferiormente.
6) Su simetría depende del valor de la constante a :
• Si a = 0 : tiene simetría par.
• Si a ≠ 0 : no tiene simetría par ni impar.
7) Su monotonía depende del valor de la constante k :
• Si k > 0 : f(x) es estrictamente creciente en (-∞ , a)
f(x) es estrictamente decreciente en (a , ∞).
• Si k < 0 : f(x) es estrictamente decreciente en (-∞ , a)
f(x) es estrictamente creciente en (a , ∞).
8) No son periódicas.
9) No tienen extremos relativos.
Ejemplos de función del tipo: k / (x - a)2
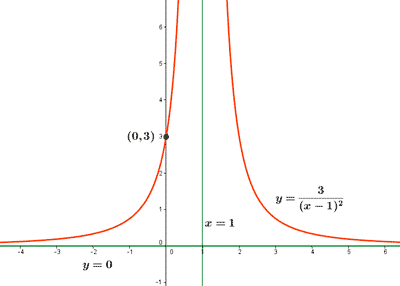
Estudiar las características de la siguiente función:
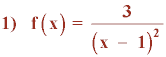
1) Los valores que anulan al denominador son:
(x - 1)2 = 0 ⇔ x - 1 = 0 ⇔ x = 1
Dom(f) = R - {1}
2) Como k = 3 > 0 : Im(f) = (0 , ∞)
3) Corta al eje de ordenadas en el punto :
k = 3 , a = 1 ⇒ (0 , 3)
4) Es discontinua en el punto : x = 1
5) Como k = 3 > 0 : está acotada inferiormente por y = 0 .
6) Como a ≠ 0 : no tiene simetría par ni impar.
7) Como k > 0 :
La función es estrictamente creciente en (-∞ , 1).
La función es estrictamente decreciente en (1 , ∞).
8) No tiene periodicidad.
9) No tiene extremos relativos.
10) Tabla de valores:
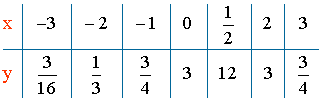
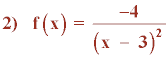
1) Los valores que anulan al denominador son:
(x - 3)2 = 0 ⇔ x - 3 = 0 ⇔ x = 3
Dom(f) = R - {3}
2) Como k = - 4 < 0 : Im(f) = (-∞, 0)
3) Corta al eje de ordenadas en el punto :
k = - 4 , a = 3 ⇒ (0 , -4/9)
4) Es discontinua en el punto : x = 3
5) Como k = - 4 < 0 : está acotada superiormente por y = 0 .
6) Como a ≠ 0 : no tiene simetría par ni impar.
7) Como k < 0 :
La función es estrictamente decreciente en (-∞ , 3).
La función es estrictamente creciente en (3 , ∞).
8) No tiene periodicidad.
9) No tiene extremos relativos.
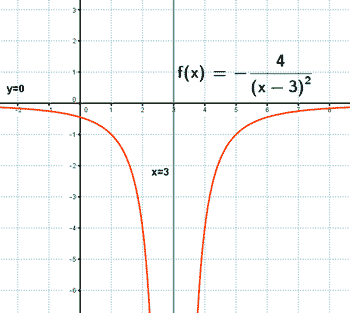


 INICIO
INICIO


