El problema de la programación lineal
Los problemas de programación lineal consisten en optimizar una función lineal (la función objetivo), que está sujeta a una serie de restricciones (sistema de inecuaciones).
La programación lineal se utiliza en multitud de problemas y permite mejorar el rendimiento en una gran variedad de situaciones. Algunos ejemplos son:
- Problemas de transporte.
- Programación de la producción: control óptimo.
- Problemas de elaboración de patrones de corte en la industria textil.
- Problemas de distribución de capital en diversas carteras.
- Problemas de mezclas de componentes en productos alimentarios.
- Optimización de semáforos.
- Redes de comunicaciones internas de empresas.
Un problema de programación lineal con dos incógnitas x e y, consiste en optimizar (calcular el máximo o el mínimo según el caso) de una función lineal llamada función objetivo. Estas funciones tienen la forma
![]()
sujeta a una serie de condiciones o restricciones establecidas mediante un sistema de inecuaciones lineales en las variables x e y:
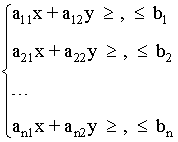
Llamaremos región factible a la solución del sistema de ecuaciones dado por las restricciones.
Para la región factible consideraremos únicamente signos de desigualdad no estrictos ≥ , ≤
La región factible puede ser acotada o no acotada.
Entre los puntos de la región factible dada por las restricciones se encontrará, si existe, la solución del problema, a la cual llamaremos solución óptima.
Puede haber:
- Una única solución óptima, que se encontrará en uno de los vértices de la región factible.
- Infinitas soluciones óptimas: Si se alcanza el valor óptimo en dos de los vértices de la región factible, entonces también son solución todos los puntos del segmento que une dichos vértices.
- Ninguna solución óptima.
Ejemplo de problema de programación lineal
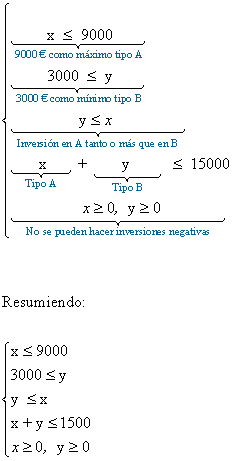
Una persona tiene 15000 € para invertir en dos tipos de acciones, A y B. El tipo A tiene un interés anual del 9% y el tipo B, del 5%. Decide invertir, como máximo, 9000 € en A, y como mínimo, 3000 € en B. Además, quiere invertir en A tanto o más que en B.
a) Calcula las condiciones o restricciones del problema de programación lineal
b) Dibuja la región factible
a) Empezamos por traducir al lenguaje de la programación lineal el enunciado del problema.
- Llamamos x al dinero invertido en acciones de tipo A.
- Llamamos y al dinero invertido en acciones de tipo B.
Las restricciones del problema son:
b) La región factible con estas restricciones sería la siguiente:
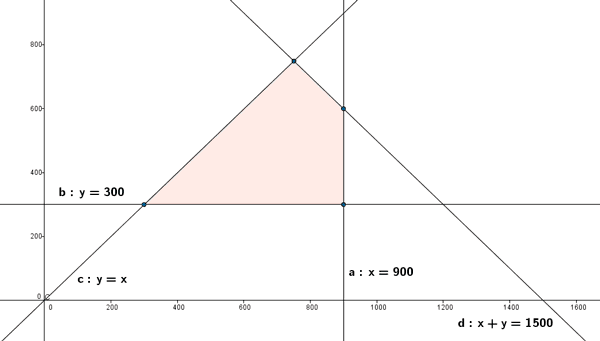
Por lo tanto, la región factible está acotada.
Por el método analítico o geométrico del tema siguiente se estudian las soluciones óptimas del problema.
Solución del problema completo: problema 11


 INICIO
INICIO

