Rango de una matriz mediante determinantes:
Método para hallar el rango de una matriz a partir de sus menores
Si en una matriz de orden m × n tomamos k filas y k columnas, se forma un determinante de orden k llamado menor de orden k.
Si a un menor de orden k se le añaden una fila y una columna cualesquiera de la matriz, se obtiene un menor de orden k+1 que se llama menor orlado.
Definimos el rango de una matriz A como el orden del mayor menor no nulo obtenido en la matriz A. Representamos el rango de la matriz A como rg(A).
Una matriz A de dimensión m × n siempre verifica que rg(A) ≤ min ( m , n )
Para calcular el rango de una matriz bastará con encontrar un menor no nulo tal que todos sus orlados den lugar a determinantes nulos.
Ejemplo de cálculo de una matriz mediante determinantes
Calcula el rango de la matriz A empleando determinantes.
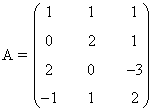
Empezamos observando que como la matriz es de orden 4 × 3, rg(A) ≤ 3. Buscamos ahora menores no nulos de los distintos órdenes:
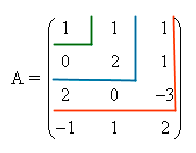
- Menor de orden 1: |a11|=1≠0 por tanto la matriz tiene al menos rango 1.
- Menor de orden 2:
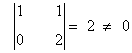
de manera que la matriz tiene al menos rango 2.
- Menor de orden 3:
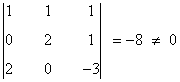
de manera que la matriz tiene rango 3, ya que 3 es el orden del mayor menor no nulo que podía obtenerse, tal como observamos al principio.
Calcular el rango de la matriz B utilizando determinantes
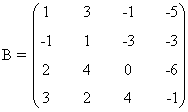
Como la matriz es de orden 4, sabemos que a lo sumo tendrá rango 4. Empezamos calculando un menor no nulo de orden 2. Tomando las dos primeras filas y las dos primeras columnas obtenemos que
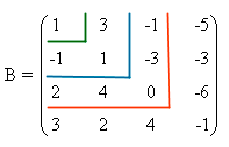
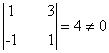
De manera que la matriz B tiene rango al menos 2. Veamos qué ocurre con el rango 3. Para ello calculamos los menores orlados respecto del menor que acabamos de tomar con el objetivo de ver si alguno de ellos es no nulo:
- Añadiendo la tercera fila y la tercera columna:
- Añadiendo la cuarta fila y la tercera columna:
- Añadiendo la cuarta fila y la cuarta columna:
- Añadiendo la tercera fila y la cuarta columna:
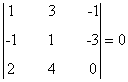
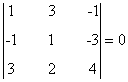
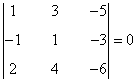
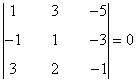
Como todos ellos son nulos obtenemos que el rg(B) < 3. Acabamos de establecer que el mayor menor no nulo es de orden 2. Por tanto rg(B) = 2.
Para matrices cuadradas es un buen método empezar calculando el determinante de la propia matriz, ya que en caso de ser no nulo, obtenemos que el rango es el propio orden de la matriz.
Encontrar el rango de la matriz C
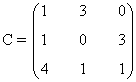
Como la matriz es de orden 3, tenemos que rg(C) ≤ 3. Observamos que
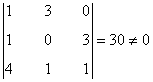
de manera que acabamos de encontrar un menor de orden 3, que era el máximo posible. Por tanto rg(C) = 3.


 INICIO
INICIO

