Problemas resueltos de cálculo del rango por determinantes
1) Encontrar el rango de la matriz C
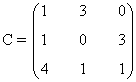
2) Calcular, utilizando determinantes, el rango de las siguientes matrices:
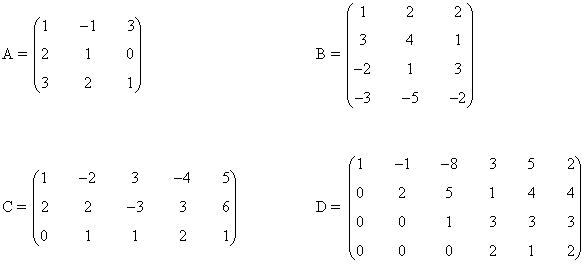
3) Calcula el rango de la matriz A empleando determinantes.
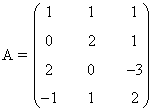
4) Calcular el rango de la matriz B utilizando determinantes
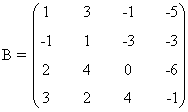
5) Estudiar el rango de las siguientes matrices utilizando determinantes:
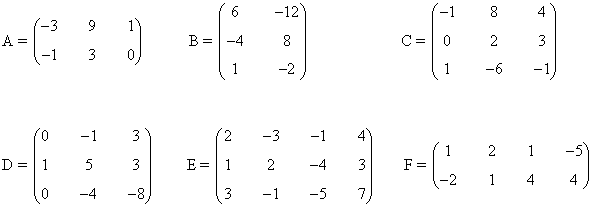
6) Hallar el rango de la siguiente matriz:
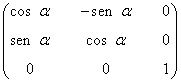
7) Escribe dos matrices de dimensión 3 × 4 que tengan, repectivamente, rangos 1, 2, 3 y 4. Razona la respuesta.
Escribe cuatro matrices de orden 4, que tengan, respectivamente, rangos 1, 2, 3 y 4. Razona la respuesta.
8) Calcula los valores de los parámetros a, b, c, para los cuales rg(B)=1, donde B es la siguiente matriz:
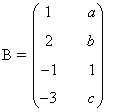
9) Calcula el rango de la matriz A según los diferentes valores del parámetro real a.
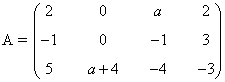
10) Calcula el rango de la matriz A según los diferentes valores del parámetro real k.
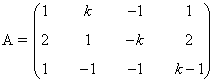
11) Estudia según los valores de x ∈ IR, el rango de la matriz A
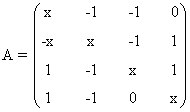
12) Estudia el rango de las siguientes matrices según el valor del parámetro que aparece en ellas:
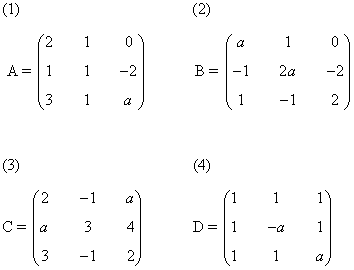
13) Estudia el rango de las siguientes matrices según el valor del parámetro a:
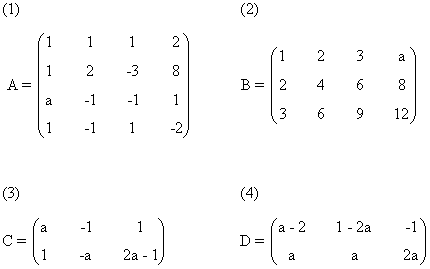
14) Si

a) Prueba que para cualquier valor de a y b, rg(A) ≥ 2
b) Determina un par de valores para los cuales rg(A) = 3
y otro par de valores para los cuales rg(A) = 4
15) Estudia el rango de la siguiente matriz para los distintos valores de a, b, y c:
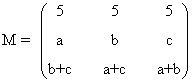
1) Encontrar el rango de la matriz C
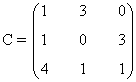
Una matriz A de dimensión m × n siempre verifica que rg(A) ≤ min ( m , n )
Como la matriz es de orden 3, tenemos que rg(C) ≤ 3. Observamos que
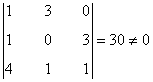
de manera que acabamos de encontrar un menor de orden 3, que era el máximo posible. Por tanto rg(C) = 3.
Para matrices cuadradas es un buen método empezar calculando el determinante de la propia matriz, ya que en caso de ser no nulo, obtenemos que el rango es el propio orden de la matriz.
el rango de la matriz es el orden del mayor menor no nulo
2) Calcular, utilizando determinantes, el rango de las siguientes matrices:
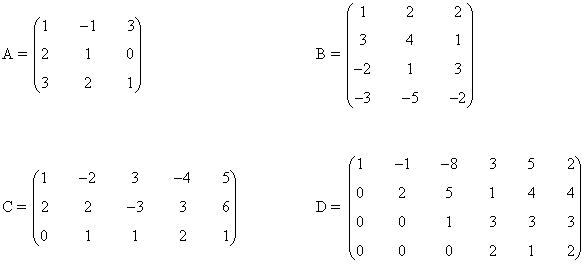
Una matriz A de dimensión m × n siempre verifica que rg(A) ≤ min ( m , n )
Empezamos por la matriz A. Como es de orden 3, sabemos que el rg(A) ≤ 3. Observamos además que
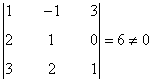
de manera que rg(A)=3.
Estudiamos ahora el caso de la matriz B. Como es de orden 4 × 3, tenemos que su rango puede ser a lo sumo 3. Observamos que
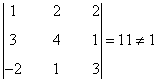
es decir, B contiene un menor de orden 3 no nulo. Esto nos dice que su rango es al menos 3. Como rg(B) ≤ 3, entonces rg(B) = 3.
Estudiamos ahora la matriz C. Como es de orden 3 × 6, tenemos que su rango puede ser a lo sumo 3. Observamos que
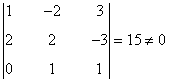
es decir, C contiene un menor de orden 3 no nulo. Esto nos dice que su rango es al menos 3. Como rg(C) ≤ 3, entonces rg(C) = 3.
Para la matriz D, como es de orden 4 × 6, tenemos que su rango puede ser a lo sumo 4. Observamos que
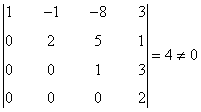
es decir, C contiene un menor de orden 4 no nulo. Esto nos dice que su rango es al menos 4. Como rg(D) ≤ 4, entonces rg(D) = 4.
el rango de la matriz es el orden del mayor menor no nulo
3) Calcula el rango de la matriz A empleando determinantes.
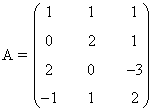
Una matriz A de dimensión m × n siempre verifica que rg(A) ≤ min ( m , n )
Empezamos observando que como la matriz es de orden 4 × 3, rg(A) ≤ 3. Buscamos ahora menores no nulos de los distintos órdenes:
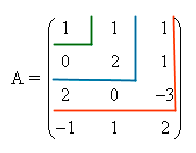
- Menor de orden 1: |a11|=1≠0 por tanto la matriz tiene al menos rango 1.
- Menor de orden 2:
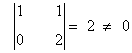
de manera que la matriz tiene al menos rango 2.
- Menor de orden 3:
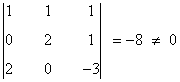
de manera que la matriz tiene rango 3, ya que 3 es el orden del mayor menor no nulo que podía obtenerse, tal como observamos al principio.
el rango de la matriz es el orden del mayor menor no nulo
4) Calcular el rango de la matriz B utilizando determinantes
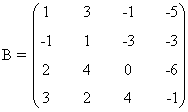
Una matriz A de dimensión m × n siempre verifica que rg(A) ≤ min ( m , n )
Como la matriz es de orden 4, sabemos que a lo sumo tendrá rango 4. Empezamos calculando un menor no nulo de orden 2. Tomando las dos primeras filas y las dos primeras columnas obtenemos que
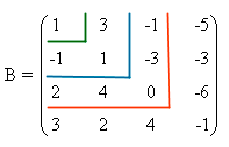
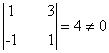
De manera que la matriz B tiene rango al menos 2. Veamos qué ocurre con el rango 3. Para ello calculamos los menores orlados respecto del menor que acabamos de tomar con el objetivo de ver si alguno de ellos es no nulo:
- Añadiendo la tercera fila y la tercera columna:
- Añadiendo la cuarta fila y la tercera columna:
- Añadiendo la cuarta fila y la cuarta columna:
- Añadiendo la tercera fila y la cuarta columna:
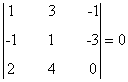
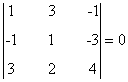
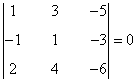
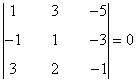
Como todos ellos son nulos obtenemos que el rg(B) < 3. Acabamos de establecer que el mayor menor no nulo es de orden 2. Por tanto rg(B) = 2.
el rango de la matriz es el orden del mayor menor no nulo
5) Estudiar el rango de las siguientes matrices utilizando determinantes:
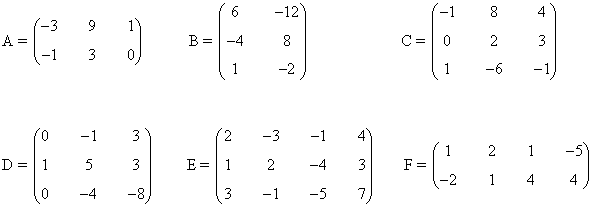
Una matriz A de dimensión m × n siempre verifica que rg(A) ≤ min ( m , n )
Empezamos por la matriz A. Dicha matriz tiene orden 2 × 3, de manera que su rango puede ser a lo sumo 2. Observamos que
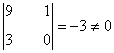
es decir, la matriz A contiene un menor de orden 2. Esto nos dice que rg(A)≥ 2. Por otra parte, el rango de A puede ser a lo sumo 2. Por tanto rg(A) = 2.
Estudiamos ahora la matriz B. Su orden es 3 × 2, por lo cual su rango puede ser como mucho 2. Utilicemos el método de orlado. Observamos que |a11| = 6 es un menor de orden 1. Calculemos sus menores orlados:
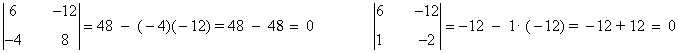
Observamos que son todos nulos. Por tanto rg(B) = 1.
Trabajamos ahora con la matriz C. Como su orden es 3, tendrá rango a lo sumo 3. Como es una matriz cuadrada conviene empezar calculando el determinante de C.
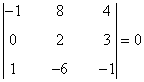
Como el determinante es nulo, buscamos si hay algún menor de orden 2 no nulo. Vemos que
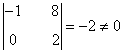
es un menor de orden 2 no nulo. Por tanto la matriz tiene rango 2.
En el caso de la matriz D, como su orden es 3 podrá tener orden como mucho 3. Dado que es una matriz cuadrada, empezamos calculando su determinante:
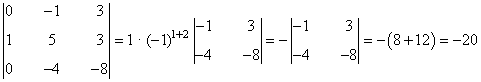
Como el determinante es no nulo, el rango de la matriz será 3.
Nos detenemos ahora a estudiar la matriz E. Vemos que su orden es 3 × 4 por lo cual su rango puede ser a lo sumo 3. Observamos que
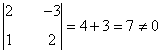
es decir, la matriz E contiene un menor de orden 2 no nulo, de manera que rg(E) ≥ 2. Estudiamos ahora los orlados de dicho menor:
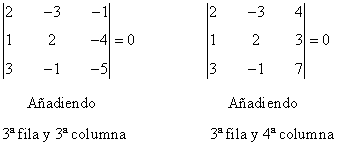
Como son ambos nulos, obtenemos que rg(E) = 2.
Para acabar, estudiamos la matriz F. Su orden es 2 × 4, de forma que su rango puede ser como mucho 2. Vemos que
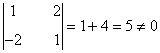
es decir, F contiene un menor de orden 2 no nulo, por lo cual rg(F) ≥ 2. Como el rango de F puede ser como mucho 2, necesariamente rg(F)=2.
el rango de la matriz es el orden del mayor menor no nulo
6) Hallar el rango de la siguiente matriz:
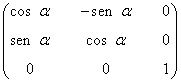
Una matriz A de dimensión m × n siempre verifica que rg(A) ≤ min ( m , n )
Observamos que
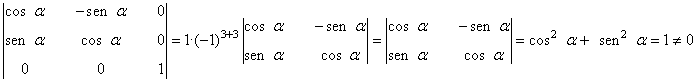
de manera que el rango de la matriz es 3.
el rango de la matriz es el orden del mayor menor no nulo
7) Escribe dos matrices de dimensión 3 × 4 que tengan, repectivamente, rangos 1, 2, 3 y 4. Razona la respuesta.
Escribe cuatro matrices de orden 4, que tengan, respectivamente, rangos 1, 2, 3 y 4. Razona la respuesta.
Una matriz A de dimensión m × n siempre verifica que rg(A) ≤ min ( m , n )
Empezamos con las matrices de dimensión 3 × 4.
- Rango 1. Consideramos la matriz
- Rango 2. Elegimos la matriz
- Rango 3. Tomamos la matriz
- Rango 4. No existe ninguna matriz 3 × 4 con rango 4, ya que el rango de estas matrices es menor o igual que 3.
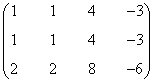
Vemos que las dos primeras filas son iguales y la tercera es el doble de cualquiera de ellas. Tenemos que todas las fillas son proporcionales a la primera de modo que solo hay una fila linealmente independiente. De esto se sigue que el rango es 1.
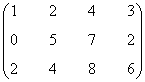
Observamos que las dos primeras filas son linealmente independientes mientras que la tercera es el doble de la primera. Consecuentemente el rango de la matriz es 2.
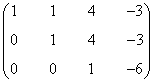
Es claro que su rango es 3 ya que el menor formado por las tres primeras columnas es no nulo.
Buscamos ahora los ejemplos para matrices de orden 4.
- Rango 1. Consideramos la matriz
- Rango 2. Elegimos la matriz
- Rango 3. Tomamos la matriz
- Rango 4. Consideramos la matriz
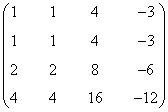
Vemos que las dos primeras columnas son iguales, la tercera es 4 veces cualquiera de ellas y la cuarta -3 veces la primera. Tenemos que todas las columnas son proporcionales a la primera de modo que solo hay una fila linealmente independiente. De esto se sigue que el rango es 1.
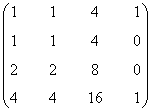
Observamos que las dos primeras columnas son iguales y que la tercera es 4 veces la primera. Por otra parte, la última columna y cualquiera de las otras son linealmente independientes. Por tanto, hay 2 vectores linealmente independientes y el rango de la matriz es 3.
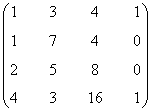
Vemos primero que
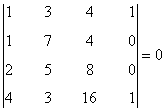
y por otra parte que
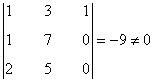
de manera que el mayor menor no nulo de la matriz tiene orden 3. Esto nos dice que la matriz tiene rango 3.
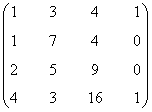
Vemos que
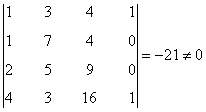
de manera que el mayor menor no nulo es de orden 4. Esto nos dice que la matriz es de rango 4.
el rango de la matriz es el orden del mayor menor no nulo
8) Calcula los valores de los parámetros a, b, c, para los cuales rg(B)=1, donde B es la siguiente matriz:
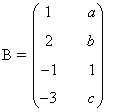
Para que el rango de la matriz B sea 1, las dos columnas de la matriz tienen que ser proporcionales. Por tanto:
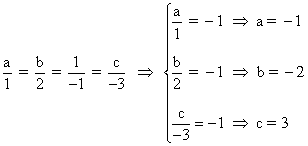
9) Calcula el rango de la matriz A según los diferentes valores del parámetro real a.
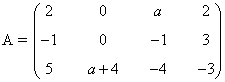
Una matriz A de dimensión m × n siempre verifica que rg(A) ≤ min ( m , n )
Empezamos viendo que el rango es al menos 2 ya que hay un menor de orden 2 no nulo:
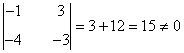
Para estudiar el rango de la matriz, calculemos ahora los menores orlados que contienen al menor que hemos fijado. El rango de la matriz será 2 cuando ambos sean nulos y 3 cuando alguno de ellos no se anule.
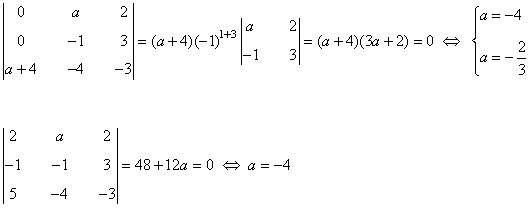
Teniendo esto en cuenta:
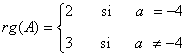
el rango de la matriz es el orden del mayor menor no nulo
10) Calcula el rango de la matriz A según los diferentes valores del parámetro real k.
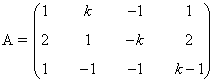
Una matriz A de dimensión m × n siempre verifica que rg(A) ≤ min ( m , n )
Empezamos viendo que el rango es al menos 2 ya que hay un menor de orden 2 no nulo:
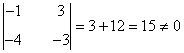
Para estudiar el rango de la matriz, calculemos ahora los menores orlados que contienen al menor que hemos fijado. El rango de la matriz será 2 cuando ambos sean nulos y 3 cuando alguno de ellos no se anule.
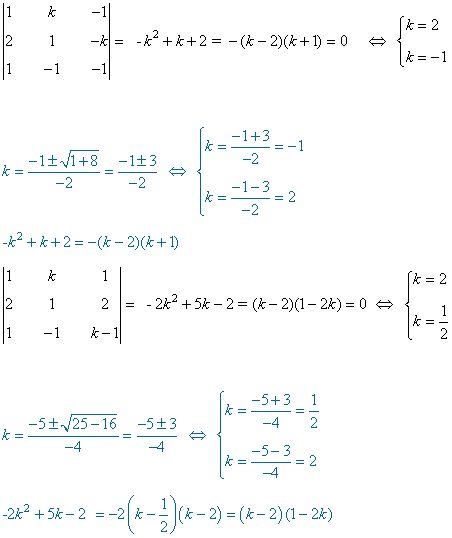
Teniendo esto en cuenta:
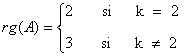
el rango de la matriz es el orden del mayor menor no nulo
11) Estudia según los valores de x ∈ IR, el rango de la matriz A
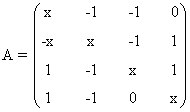
Una matriz A de dimensión m × n siempre verifica que rg(A) ≤ min ( m , n )
Vamos a empezar calculando el determinante de A. Sabemos que al sumar a una columna otra columna el valor del determinante no cambia. En nuestro caso, si sumamos la segunda columna a la primera el valor de |A| no varía. Teniendo esto en cuenta:
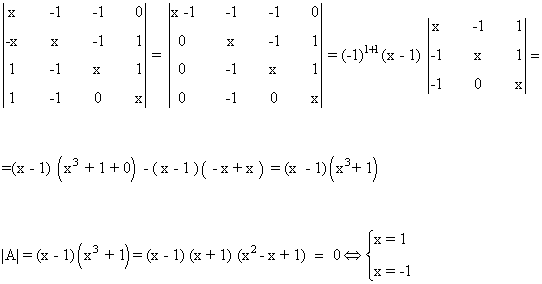
Por tanto, sabemos que si x es distinto de 1 y de -1, rg(A) = 4. Veamos qué ocurre si x = 1 y si x = -1.
Si x = 1, tenemos que
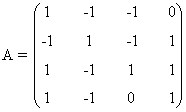
y esta matriz contiene un menor de orden 3 no nulo:
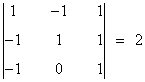
por lo cual rg(A) = 3.
Por otra parte, si x = -1, se tiene que la matriz transformada resulta ser
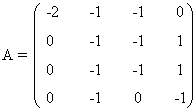
de manera que el menor
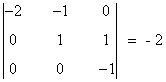
es no nulo. Por lo cual rg(A)=3. En resumen:
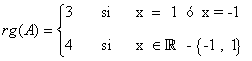
el rango de la matriz es el orden del mayor menor no nulo
12) Estudia el rango de las siguientes matrices según el valor del parámetro que aparece en ellas:
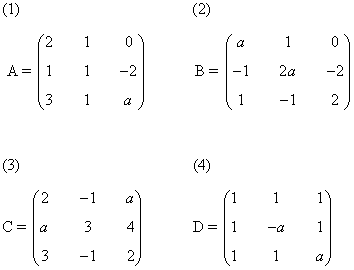
Una matriz A de dimensión m × n siempre verifica que rg(A) ≤ min ( m , n )
(1)
Empezamos por A. Como la matriz es cuadrada conviene empezar calculando |A| y viendo cuando se anula en función del parámetro a:
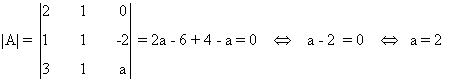
Como vemos, esto ocurre si y sólo si a = 2. Por tanto si a ≠ 2, tenemos que rg(A) = 2. Si a = 2, entonces |A| = 0, de manera que el rango puede ser a lo sumo 2. En este caso,
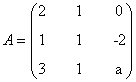
y vemos que hay un menor de orden 2 no nulo:
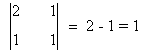
Por tanto rg(A) = 2 cuando a = 2. En resumen:
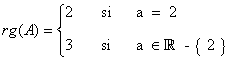
(2)
Seguimos por la matriz B. Como la matriz es cuadrada conviene empezar calculando |B| y viendo cuando se anula en función del parámetro a:
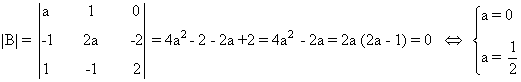
Como vemos, esto ocurre si y sólo si a = 0 o a = 1/2. Por tanto si a ∉ {1/2 , 0}, tenemos que rg(B) = 3. Si a = 0 o a = 1/2, entonces |B| = 0, de manera que el rango puede ser a lo sumo 2. Estudiemos estos casos. Si a = 0,
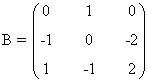
y vemos que hay un menor de orden 2 no nulo:
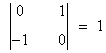
Por tanto rg(B) = 2 cuando a = 0.
Si a = 1/2, entonces
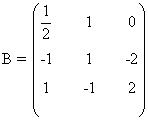
y vemos que hay un menor de orden 2 no nulo:
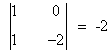
Por tanto rg(B) = 2 cuando a = 1/2.
En resumen:
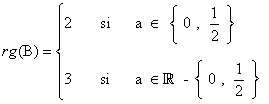
(3)
Estudiamos ahora el caso de la matriz C. Como la matriz es cuadrada conviene empezar calculando |C| y viendo cuando se anula en función del parámetro a:
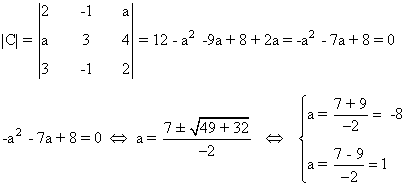
Como vemos, esto ocurre si y sólo si a = -8 o a = 1. Por tanto si a ∉ {1 , -8}, tenemos que rg(C) = 3. Si a = 1 o a = -8, entonces |C| = 0, de manera que el rango puede ser a lo sumo 2.
Nos percatamos ahora de que existe un menor no nulo de orden 2 que no depende del valor de a:
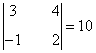
de manera que rg(C) ≥ 2 para todo a. En particular si a = -8 o a = 1, sabemos que el rango es necesariamente menor o igual que 2, de manera que rg(C) = 2 cuando a = -8 o a = 1.
En resumen:
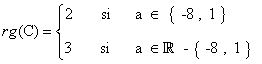
(4)
Acabamos el ejercicio estudiando el rango de la matriz D. Nuevamente, como la matriz es cuadrada conviene empezar calculando |D| y viendo cuando se anula en función del parámetro a:
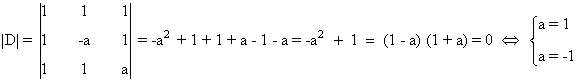
Como vemos, esto ocurre si y sólo si a = -1 o a = 1. Por tanto si a ∉ {1 , -1}, tenemos que rg(A) = 3. Si a = 1 o a = -1, entonces |D| = 0, de manera que el rango puede ser a lo sumo 2. Estudiemos el caso en que a = -1. En este caso,
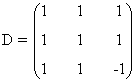
y vemos que hay un menor de orden 2 no nulo:
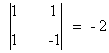
Por tanto rg(A) = 2 cuando a = -1.
Estudiamos ahora el caso en que a = 1. En este caso,
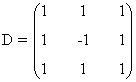
y vemos que hay un menor de orden 2 no nulo:
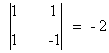
Por tanto rg(A) = 2 cuando a = 1.
En resumen:
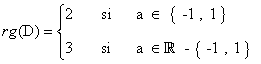
el rango de la matriz es el orden del mayor menor no nulo
13) Estudia el rango de las siguientes matrices según el valor del parámetro a:
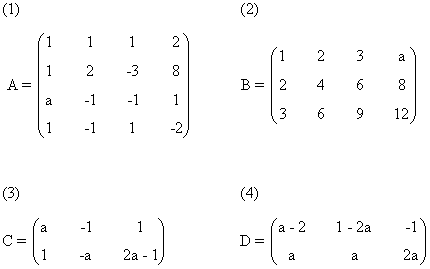
Una matriz A de dimensión m × n siempre verifica que rg(A) ≤ min ( m , n )
(1)
Empezamos por A. Observamos que el menor de orden 3
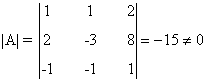
que no depende de a es no nulo, por lo cual rg(A) ≥ 3 para todo a. Calculamos ahora el determinante de A para encontrar los valores del parámetro para los cuales dicho determinante se anula:

Teniendo en cuenta todo lo anterior
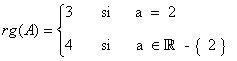
(2)
Seguimos por la matriz B. A simple vista, puede verse que si a = 4, las tres filas son proporcionales, de manera que rg(B) = 1.
Si a ≠ 4, entonces vemos que
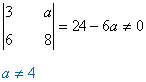
Calculamos ahora los menores orlados de este menor:

Como son todos nulos, rg(B) = 2. En resumen:
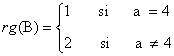
(3)
Estudiamos ahora el caso de la matriz C. Como es una matriz de orden 2 × 3 su rango es a lo sumo 2. Empezamos considerando el menor de orden 2 constituido por las dos primeras filas y las dos primeras columnas. Vemos que
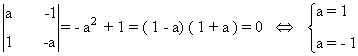
Si a ∉ { -1 , 1 } entonces rg(A) = 2. Nos queda determinar qué ocurre si a = 1 o si a = - 1.
Si a = 1 entonces
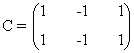
y como las dos filas son iguales y no nulas rg(C) = 1.
Si a = -1 entonces
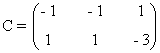
Observamos que en este caso C contiene un menor de orden 2 no nulo:
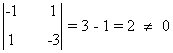
de manera que rg(C) =2. En resumen:
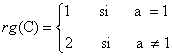
(4)
Para acabar estudiamos el rango de la matriz D. Como es una matriz de orden 2 × 3 su rango es a lo sumo 2. Empezamos considerando el menor de orden 2 constituido por las dos primeras filas y las dos primeras columnas. Vemos que
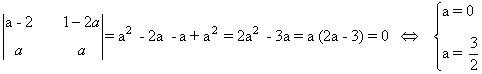
Si a ∉ { 0 , 3/2 } entonces rg(A) = 2. Nos queda determinar qué ocurre si a = 0 o si a = 3/2.
Si a = 0 entonces
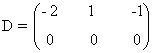
Como hay una fila nula y otra fila no nula, rg(D) = 1.
Si a = 3/2 entonces

Observamos que en este caso D contiene un menor de orden 2 no nulo:
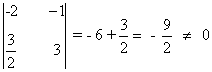
de manera que rg(D) =2. En resumen:
el rango de la matriz es el orden del mayor menor no nulo
14) Si

a) Prueba que para cualquier valor de a y b, rg(A) ≥ 2
b) Determina un par de valores para los cuales rg(A) = 3 y otro par de valores para los cuales rg(A) = 4
Una matriz A de dimensión m × n siempre verifica que rg(A) ≤ min ( m , n )
(a)
Tomamos los siguientes menores:
- El formado por las dos primeras columnas y las filas segunda y tercera:
- El formado por la primera y la última fila y las dos últimas columnas:
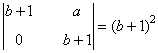
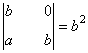
Observamos que b2 y (b+1)2 no pueden anularse a la vez. Esto nos dice que para cualquier b, al menos uno de los dos menores de orden dos anteriores es no nulo, de manera que, de manera que rg(A) ≥ 2
(b)
En esta pregunta damos dos pares de valores en las condiciones que se nos piden, pero no tienen por qué ser los únicos pares de valores válidos, es decir, puede haber más respuestas correctas.
Empezamos calculando el determinante de la matriz A.
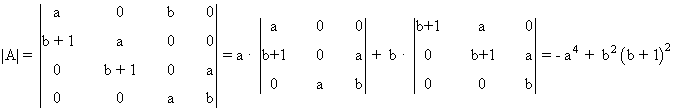
Para que el rango sea 4, basta con que |A| ≠ 0. Esto ocurre por ejemplo si a = 1 y b =0.
Para que el rango sea 3, necesitamos que |A| = 0. Esto nos es equivalente a que a4 = b2(b+1)2. Vemos que uno de los menores de orden 3 es el formado por la primera, la segunda y la cuarta fila y por la primera, la segunda y la tercera columna y que se verifica que
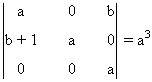
Si tomamos a = √2, este menor es no nulo. Eligiendo además b = 1,
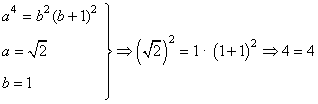
es decir |A| = 0, de manera que rg(A) = 3.
En resumen:
- Si tomamos a = 1 y b = 0, entonces rg(A) = 4.
- Si elegimos a = √2 y b = 1, entonces rg(A) = 3.
el rango de la matriz es el orden del mayor menor no nulo
15) Estudia el rango de la siguiente matriz para los distintos valores de a, b, y c:
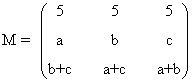
Una matriz A de dimensión m × n siempre verifica que rg(A) ≤ min ( m , n )
Empezamos calculando el determinante de M
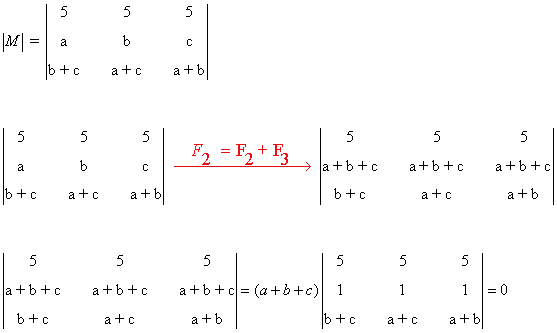
ya que las dos primeras filas son proporcionales. Consecuentemente, rg(M) ≤ 2.
Trabajamos ahora con los menores de orden 2. Fijándonos en las dos primeras filas, estos son:
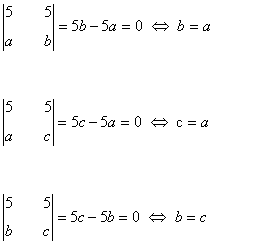
Si a = b = c, la matriz tiene el siguiente aspecto:
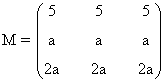
Si a es nulo, entonces rg(A) = 1 ya que la matriz solo tiene una fila linealmente independiente. Si a ≠ 0 también rg(A) = 1 ya que las tres filas son proporcionales.
Si a ≠b, a ≠c ó b ≠c entonces, rg(M) = 2, ya que alguno de los menores de orden 2 anteriores es no nulo.
el rango de la matriz es el orden del mayor menor no nulo


 INICIO
INICIO