Ejercicios resueltos de sistemas de ecuaciones exponenciales
Resuelve el siguiente sistema de ecuaciones exponenciales:
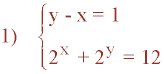
Despejamos y en la primera ecuación y lo sustituimos en la segunda:
y = 1 - x
2x + 21+x = 12
2x + 2·2x = 12
(1 + 2)·2x = 12
3·2x = 12
2x = 4
2x = 22
x = 2
Sustituimos el valor de x :
y = 1 + x = 1 + 2
y = 3
Resuelve el siguiente sistema de ecuaciones exponenciales:
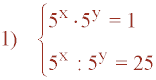
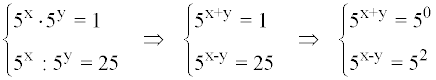
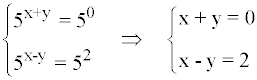
Resolvemos el sistema de ecuaciones lineales resultante por el método de reducción:
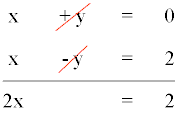
Resolviendo la ecuación tenemos que:
x = 1
Sustituyendo en la primera ecuación del sistema lineal tenemos que:
1 + y = 0
y = - 1
Resuelve el siguiente sistema de ecuaciones exponenciales:
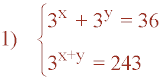
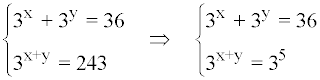
De la segunda ecuación exponencial tenemos que:
x + y = 5
y = 5 - x
Sustituyendo el valor de y en la primera ecuación tenemos que:
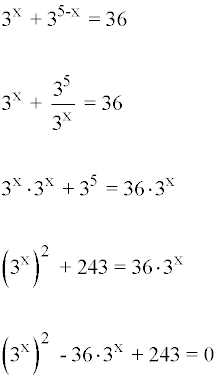
Hacemos el siguiente cambio de variable:
t = 3x
Obtenemos la ecuación de segundo grado:
t2 - 36t + 243 = 0
Resolvemos la ecuación de segundo grado:
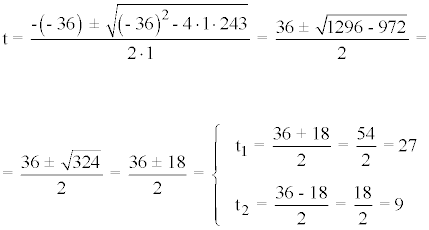
Deshacemos el cambio de variable para hallar las soluciones del sistema:
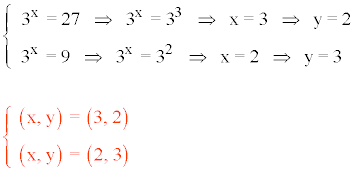
Resuelve el siguiente sistema de ecuaciones exponenciales:
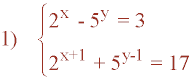
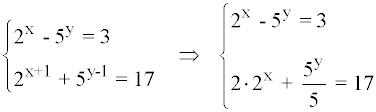
Hacemos los siguientes cambios de variable:
2x = u
5y = v
Obteniendo el siguiente sistema de ecuaciones lineales:
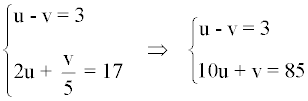
Resolvemos el sistema mediante el método de reducción:
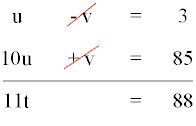
Resolviendo la ecuacion tenemos que:
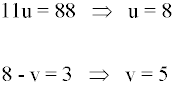
Deshacemos el cambio de variable para hallar las soluciones:
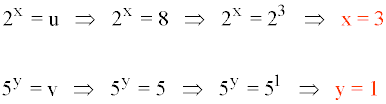
Resuelve el siguiente sistema de ecuaciones exponenciales:
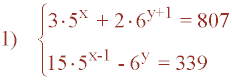
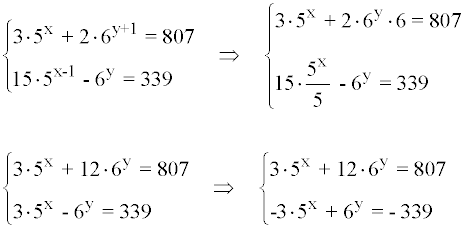
Utilizamos el método de reducción:
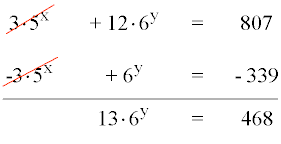
Resolvemos la ecuación exponencial para hallar las soluciones:
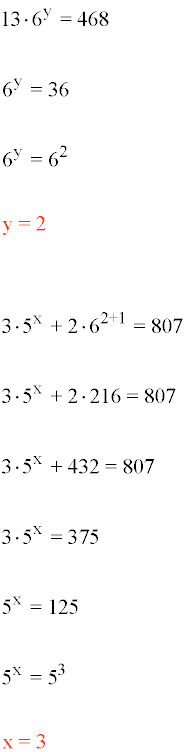


 INICIO
INICIO