Ejercicios resueltos de sistemas de ecuaciones no lineales con dos incógnitas
Resuelve los siguientes sistemas no lineales con dos incógnitas:
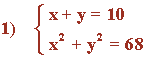
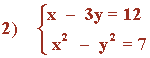
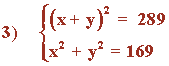
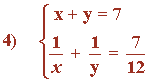
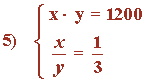
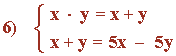
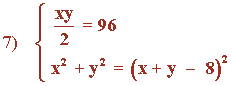
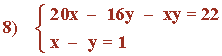
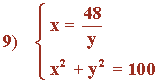
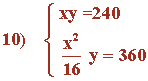
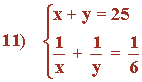
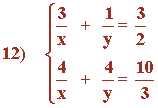
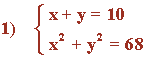
Despejamos la variable x en la primera ecuación: x + y = 10 ⇔ x = 10 - y
Sustituimos en la segunda ecuación:
x2 + y2 = 68 ⇒ (10 - y)2 + y2 = 68 ⇒ 100 - 20y + y2 + y2 = 68 ⇒ 2y2 - 20y + 32 = 0
Simpificamos la ecuación dividiendo entre 2 : y2 - 10y + 16 = 0
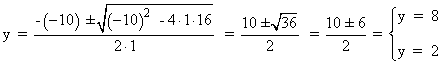
Si y = 8 ⇒ x = 10 - y = 10 - 8 = 2
Si y = 2 ⇒ x = 10 - y = 10 - 2 = 8
El sistema tiene dos soluciones: x1 = 2 , y1 = 8 ; x2 = 8 , y2 = 2
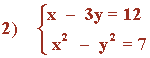
Despejamos la incógnita y de la primera ecuación y sustituimos su valor en la segunda ecuación:
x = 12 + 3y
(12 + 3y)2 - y2 = 7
144 + 72y + 9y2 - y2 = 7
8y2 + 72y + 137 = 0
A continuación resolvemos la ecuación de segundo grado:
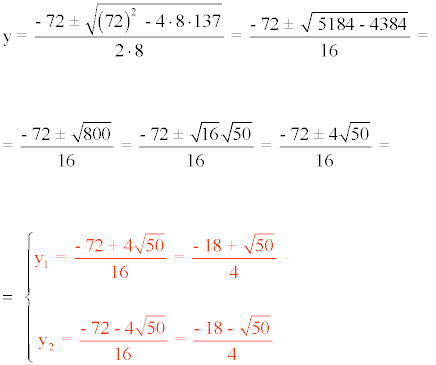
Por último sustituimos y1 e y2 en la primera ecuación del sistema:
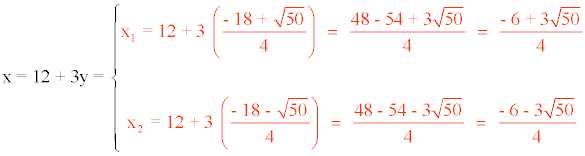
Por lo tanto las soluciones son:
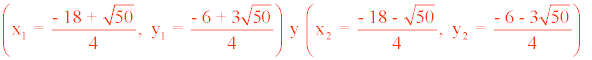
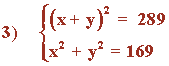
En primer lugar desarrollamos la igualdad notable de la primera ecuación:
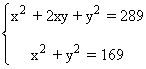
Multiplicamos la segunda ecuación por - 1 y aplicamos el método de reducción:
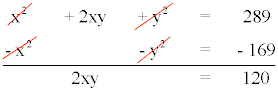
Despejamos la incógnita y y la sustituimos en la segunda ecuación del sistema:
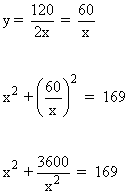
Multiplicamos cada término de la expresión por x2 :
x4 + 3600 = 169x2
x4 - 169x2 + 3600 = 0
Para resolver la ecuación bicuadrada realizamos un cambio de variable:
x2 = t
Resolvemos la siguiente ecuación de segundo grado:
t2 - 169t + 3600 = 0
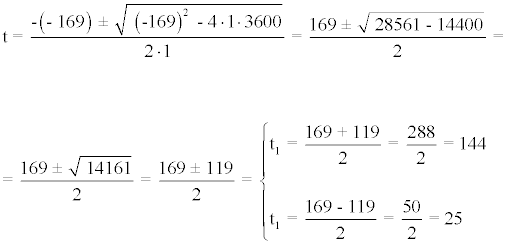
Deshacemos el cambio de variable para hallar las soluciones para x :
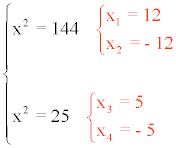
Despejando la incógnita y :
![]()
Por lo tanto las soluciones del sistema son:
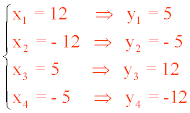
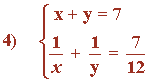
Resolvemos el sistema mediante el método de sustitución:
x + y = 7 ⇔ y = 7 - x
![]()
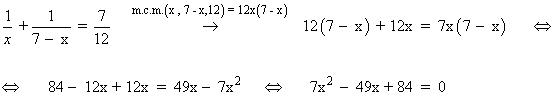
Simplificamos la ecuación dividiendo entre m.c.d.(7,49,84) = 7
7x2 - 49x + 84 = 0 ⇔ x2 - 7x + 12 = 0
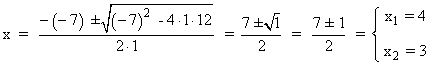
Sustituimos los valores encontrados para calcular el valor de y :
Si x = 4 , entonces: y = 7 - x = 7 - 4 = 3
Si x = 3 , entonces: y = 7 - x = 7 - 3 = 4
Los números pedidos son 3 y 4.
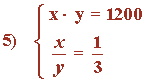
Despejamos la variable y de la segunda ecuación:
![]()
Sustituimos en la primera ecuación y resolvemos:
x · y = 1200 ⇒ x · (3x) = 1200 ⇒ 3x2 = 1200 ⇒ x2 = 400 ⇒ x = 20
Sustuimos el valor de x en la segunda ecuación para hallar el valor de y :
Si x = 20 ⇒ y = 3x = 3 · 20 = 60
El sistema tiene una única solución: x = 20 , y = 60
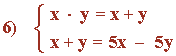
Resolvemos el sistema mediante sustitución.
Despejamos la variable y de la segunda ecuación:
x + y = 5x - 5y ⇔ 6y = 4x ⇔ y = 2x/3
Sustituimos en la primera ecuación y resolvemos:
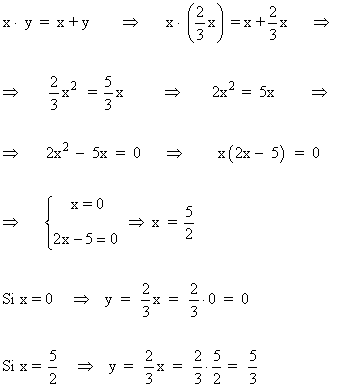
El sistema tiene dos soluciones: x = 0 e y = 0 ; x = 5/2 e y = 5/3
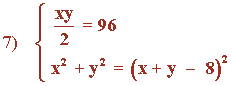
Simplificamos ambas ecuaciones:
xy/2 = 96 ⇔ xy = 192
x2 + y2 = (x - y - 8)2 ⇔ x2 + y2 = x2 + y2 + 64 + 2xy - 16x - 16y ⇔ 0 = 64 + 2xy - 16x - 16y ⇔ 16x + 16y - 2xy = 64
Como xy = 192 , la segunda ecuación queda:
16x + 16y - 2·192 = 64 ⇔ 16x + 16y - 384 = 64 ⇔ 16x + 16y = 448 ⇔ x + y = 28
Resolvemos el sistema mediante sustitución. Despejamos la variable x en la primera ecuación y sustituimos en la segunda:
xy = 192 ⇒ x = 192/y
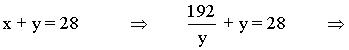
![]()
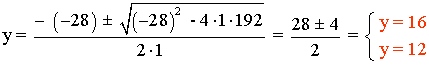
Si y = 16 ⇒ x = 192/y = 12
Si y = 12 ⇒ x = 192/y = 16
La soluciones son: x1 = 12 , y1 = 16 ; x2 = 16 , y2 = 12
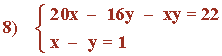
Resolvemos el sistema por el método de sustitución despejando la incógnita x de la segunda ecuación:
x - y = 1 ⇔ x = 1 + y
20x - 16y - xy = 22 ⇒ 20(1 + y) - 16y - (1 + y)y = 22 ⇒ 20 + 20y - 16y - y - y2 = 22 ⇒ y2 - 3y + 2 = 0
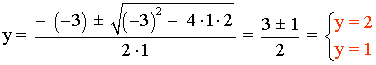
Si y = 2 ⇒ x = 1 + y = 3
Si y = 1 ⇒ x = 1 + y = 2
El sistema tiene dos soluciones: x1 = 3 , y1 = 2 ; x2 = 2 , y2 = 1
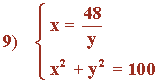
Lo resolvemos mediante el método de sustitución.
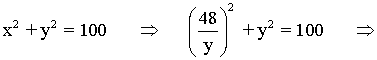
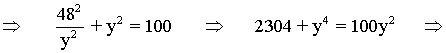
![]()
Se trata de una ecuación bicuadrática. Para resolverla hacemos el cambio de variable: z = y2
Nos queda una ecuación de segundo grado: z2 - 100z + 2304 = 0
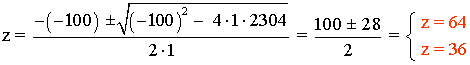
Si z = 64 ⇒ z = y2 ⇒ y = ±√z = ±√64 = ±8
Si z = 36 ⇒ z = y2 ⇒ y = ±√z = ±√36 = ±6
Sustituimos para calcular el valor de x en cada caso:
Si y = 8 ⇒ x = 48/y = 48/8 = 6
Si y = -8 ⇒ x = 48/y = 48/-8 = -6
Si y = 6 ⇒ x = 48/y = 48/6 = 8
Si y = -6 ⇒ x = 48/y = 48/-6 = -8
El sistema tiene cuatro soluciones:
x1 = 6 , y1 = 8 ; x2 = -6 , y2 = -8 ; x3 = 8 , y3 = 6 ; x4 = -8 , y4 = -6
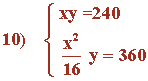
Aplicamos el método de igualación despejando la variable y en ambas ecuaciones:
![]()
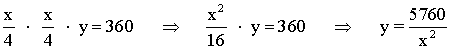
Igualamos ambos resultados:
![]()
![]()
![]()
Como x ≠ 0 , necesariamente: 240x - 5760 = 0 ⇔ 240x = 5760 ⇔ x = 24
Si x = 24 ⇒ y = 240/x = 10
La solución del sistema es: x = 24 , y = 10
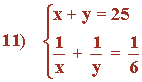
Resolvemos el sistema mediante sustitución.
Despejamos la variable x de la primera ecuación:
x + y = 25 ⇒ y = 25 - x
Sustituimos por y = 25 - x y resolvemos:
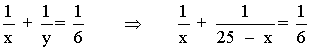
Aplicamos: m.c.m.(x, 25 - x , 6) = 6x(25 - x)
![]()
![]()
![]()
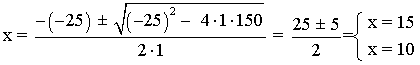
Si x = 15 ⇒ y = 25 - x = 10
Si x = 10 ⇒ y = 25 - 10 = 15
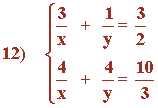
Realizamos los siguientes cambios de variable:
![]()
De esta forma obtenemos el siguiente sistema:
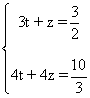
A continuación quitamos denominadores:
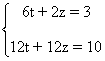
Resolvemos el sistema de ecuaciones lineales por el método de reducción:
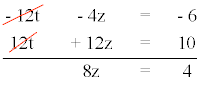
Despejando la ecuación resultante tenemos que:
z = 1/2
Sustituimos el valor de z para calcular t :
6t + 2z = 3
6t + 1 = 3
6t = 2
t = 1/3
Por último tenemos que deshacer el cambio de variable:
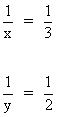
Por lo tanto las soluciones son:
x = 3
y = 2


 INICIO
INICIO