Ejercicios resueltos de sistemas de ecuaciones lineales con tres incógnitas
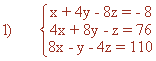
Multiplicando la primera ecuación por - 4 y sumando la segunda ecuación obtenemos:
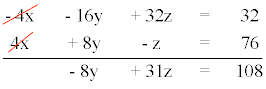
Por otra parte, multiplicando la primera ecuación por - 8 y sumando la tercera ecuación obtenemos:
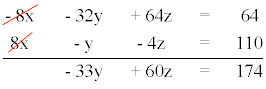
De esta forma, aplicando dos veces el método de reducción, obtenemos un nuevo sistema de ecuaciones lineales con dos incógnitas.
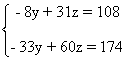
A continuación resolvemos el sistema utilizando el método de igualación:
Despejando la incógnita z en ambas ecuaciones obtenemos un nuevo sistema:
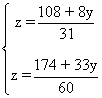
Igualando ambas ecuaciones se obtiene:
![]()
Quitamos denominadores multiplicando en cruz:
60(108 + 8y) = 31(174 + 33y)
6480 + 480y = 5394 + 1023y
1086 = 543y
y = 2
Sustituyendo el valor de y en la primera ecuación del anterior sistema obtenemos el valor de z.
![]()
z = 4
Por último, para obtener el valor de x sustituimos las soluciones obtenidas para y y para z.
x + 4y - 8z = -8
x = - 8 - 4y + 8z = - 8 - 8 + 32
x = 16
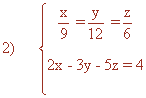
De la primera ecuación del sistema obtenemos que:
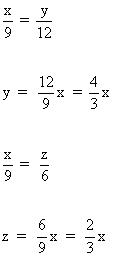
Sustituyendo los valores de y y de z en la segunda ecuación:
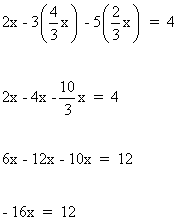
![]()
Sustituyendo el valor de x en la primera ecuación:
![]()
![]()
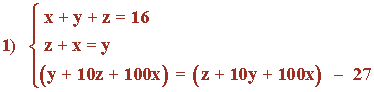
Simplificamos el sistema:
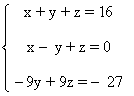
Vamos a aplicar el método de reducción en las dos primeras ecuaciones, le restamos a la primera la segunda ecuación:
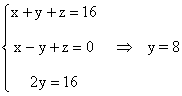
Si y = 8 , por la tercera ecuación del sistema tenemos:
-9y + 9z = -27 ⇒ -9·8 + 9z = -27 ⇒ 9z = -27 + 72 ⇒ 9z = 45 ⇒ z = 5
Si y = 8 , z = 5 , despejando la variable x en la segunda ecuación tenemos:
x - y + z = 0 ⇒ x = y - z = 8 - 5 = 3
La solución del sistema es: x = 3 , y = 8 , z = 5
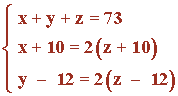
Simplificando el sistema obtenemos el siguiente:
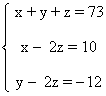
Despejamos las variables x e y en la segunda y tercera ecuación respectivamente, y después sustituimos en la primera:
x - 2z = 10 ⇔ x = 10 + 2z
y - 2z = -12 ⇔ y = 2z - 12
x + y + z = 73 ⇒ (10 + 2z) + (2z - 12) + z = 73 ⇒ 5z - 2 = 73 ⇒ 5z = 75 ⇒ z = 15
Si z = 15 ⇒ x = 10 + 2z = 10 + 2·15 = 40
Si z = 15 ⇒ y = 2z - 12 = 2·15 - 12 = 18
La solución del sistema es: x = 40 , y = 18 , z = 15
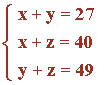
Resolvemos el sistema por el método de reducción:
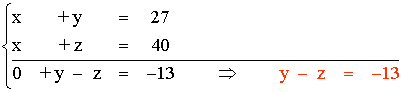
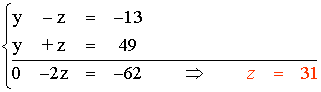
Si z = 31 ⇒ y - z = - 13 ⇒ y = - 13 + z = - 13 + 31 = 18
Si y = 18 ⇒ x + y = 27 ⇒ x = 27 - y = 27 - 18 = 9
La solución del sistema es: x = 9 , y = 18 , z = 31
En estas ecuaciones las incógnitas se representan con las letras x , y , z.
Mientras que las letras a , b , c , m , n se utilizan como constantes.
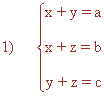
Despejamos la incógnita y de la primera ecuación:
y = a - x
Despejamos la incógnita z de la segunda ecuación:
z = b - x
Sustituimos el valor de y y de z en la tercera ecuación:
a - x + b - x = c
a + b - c = 2x
![]()
Sustituyendo el valor de x en la primera ecuación tenemos que:
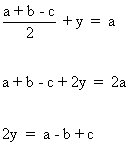
![]()
Sustituyendo el valor de y en la tercera ecuación tenemos que:
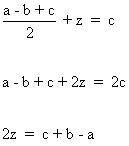
![]()


 INICIO
INICIO