Ejercicios resueltos de sistemas de ecuaciones lineales con dos incógnitas

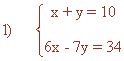
Despejando   x   en la primera ecuación y sustituyendo en la segunda, obtenemos:

y = 10 - x

6x - 7(10 - x) = 34

6x - 70 + 7x = 34

13x = 104

Por lo tanto, resolviendo la ecuación:

x = 8

Y sustituyendo el valor de   x   en la primera ecuación, tenemos que:

y = 10 - x

y = 2

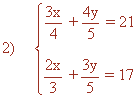
m.c.m. (4, 5) = 20

m.c.m. (3, 5) = 15

Quitando denominadores tenemos el siguiente sistema de ecuaciones:

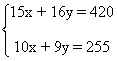
Despejando   x   en la primera ecuación y sustituyendo en la segunda, obtenemos:

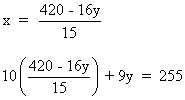
Quitamos denominadores multiplicando cada miembro de la ecuación por 15.

10(420 - 16y) + 135y = 3825

4200 - 160y + 135y = 3825

- 25y = - 375

y = 15

Y sustituyendo el valor de   x   en la primera ecuación, tenemos que:

x = 12

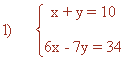
Despejando la incógnita   x   en ambas ecuaciones obtenemos el siguiente sistema:

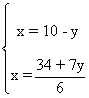
Mediante igualación, tenemos que:

6(10 - y) = 34 + 7y

60 - 6y = 34 + 7y

26 = 13y

y = 2

Por lo tanto, tenemos que:

x = 10 - y

x = 8

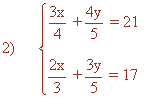
m.c.m. (4, 5) = 20

m.c.m. (3, 5) = 15

Quitando denominadores tenemos el siguiente sistema de ecuaciones:

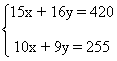
Despejando la incógnita   x   en ambas ecuaciones obtenemos el siguiente sistema:

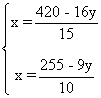
Mediante igualación, tenemos que:

m.c.m. (15, 10) = 30

Quitando denominadores tenemos que:

2(420 - 16y) = 3(255 - 9y)

840 - 32y = 765 - 27y

75 = 5y

y = 15

Y sustituyendo el valor de   x   en la primera ecuación:

x = 12

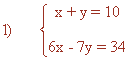
Multiplicando la primera ecuación por 7, tenemos que:

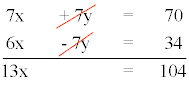
Resolviendo la ecuación obtenemos que:

x = 8

Sustituyendo el valor de   x   en la primera ecuación del sistema, obtenemos el valor para   y:

y = 10 - x

y = 2

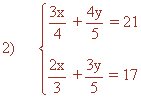
m.c.m. (4, 5) = 20

m.c.m. (3, 5) = 15

Quitando denominadores tenemos el siguiente sistema de ecuaciones:

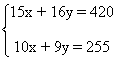
Multiplicamos la primera ecuación por   2   y la segunda ecuación por   - 3.

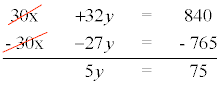
Resolviendo la ecuación tenemos que:

y = 15

Y sustituyendo el valor de   x   en la primera ecuación:

x = 12

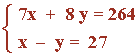
Resolvemos el sistema mediante el método de reducción:

Multiplicamos por 8 la segunda ecuación.

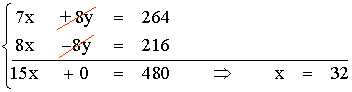
Si  x = 32    ⇒    y = x - 27 = 32 - 27 = 5

La solución del sistema es:    x = 32  ,  y = 5

 

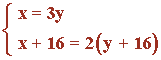
Lo resolvemos por el método de sustitución, pues ya tenemos la variable x despejada en la primera ecuación. Primero simplificamos la segunda ecuación, después, sustituimos por  x = 3y:

            x + 16 = 2(y + 16)    ⇒    x + 16 = 2y + 32    ⇒    x - 2y = 32 - 16    ⇒    x - 2y = 16

            x - 2y = 16    ⇒    3y - 2y = 16    ⇒    y = 16

Si  y = 16    ⇒    x = 3y = 3·16 = 48

La solución del sistema es: x = 48 , y = 16