Problemas resueltos de vectores
1 ) Hallar las coordenadas de un vector v ortogonal a u (5,3) y que mida el doble de u
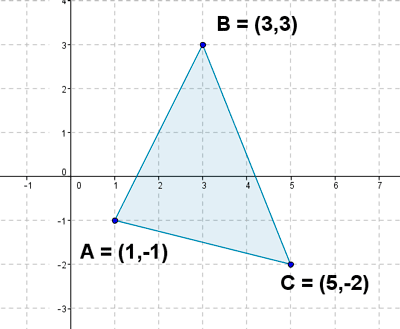
2 ) Dado el triángulo de vértices A (1,-1), B (3,3) y C (5,-2):
a ) Hallar la medida de los lados.
b ) Halla la medida de los ángulos.
3 ) Dado un vector u (2,1) y v (1,3), halla el vector w tal que w·u = 1 y w sea perpendicular a v.
4 ) Halla el valor que debe tener k para que los siguientes vectores

sean perpendiculares, siendo:
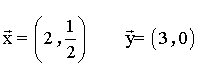
5 ) Dados los vectores a = 2u + v y b = -u + xv, siendo:
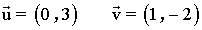
Hallar el valor de x de modo que (a+b) sea ortogonal (a-b ).
6 ) Dados los vectores:

Hallar el valor de x e y de modo que |u| = 5 y u sea perpendicular respecto de v.
7 ) De los vectores u y v sabemos que |u|=2 y |v|=6 y que forman un ángulo de 240º. Calcular:
a ) |u+v|
b ) |u-v|
c ) (u+v)·(u-v)
8 ) Halla un vector u de módulo √6 y que forme con v(1,-2) un ángulo de 60º.
9 ) Si |u|=5 y ( u + v )·( u - v )=-10 , halla |v|.
10 ) Sabiendo que |u|=2 , |v|=6 , u y v son perpendicualares. Hallar:
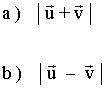
11 ) Calcular las coordenadas de cierto vector u, sabiendo que forma un ángulo de 60º con v ( 1 , 2 ) y que los módulos de ambos son iguales.
12 ) Sabiendo que:
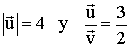
Calular u·v
13 ) Sabiendo que |u|= 3 y u = - 5v. Calular u·v
14 ) Dados los vectores u ( 3 , 1 ) y v ( 2 , -1 ). Calcular la proyección de u sobre v y la de v sobre u.
15 ) Determina un vector u que forme con v ( -2 , -4 ) un ángulo de 30º y tal que |a|=√2|b|
16 ) Dado el vector libre u ( 5 , 3 ). Calcular el vector libre v que tiene la misma dirección que u, distinto sentido y módulo igual a la unidad.
1 ) Hallar las coordenadas de un vector v ortogonal a u (5,3) y que mida el doble de u
2 ) Dado el triángulo de vértices A (1,-1), B (3,3) y C (5,-2):
a ) Hallar la medida de los lados.
b ) Halla la medida de los ángulos.
3 ) Dado un vector u (2,1) y v (1,3), halla el vector w tal que w·u = 1 y w sea perpendicular a v.
4 ) Halla el valor que debe tener k para que los siguientes vectores

sean perpendiculares, siendo:
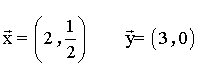
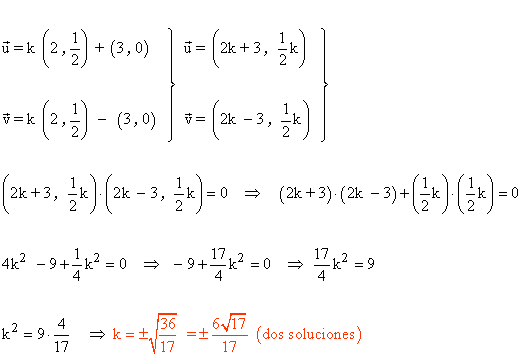
5 ) Dados los vectores a = 2u + v y b = -u + xv, siendo:
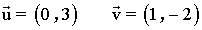
Hallar el valor de x de modo que (a+b) sea ortogonal (a-b ).
6 ) Dados los vectores:

Hallar el valor de x e y de modo que |u| = 5 y u sea perpendicular respecto de v.
7 ) De los vectores u y v sabemos que |u|=2 y |v|=6 y que forman un ángulo de 240º. Calcular:
a ) |u+v|
b ) |u-v|
c ) (u+v)·(u-v)
8 ) Halla un vector u de módulo √6 y que forme con v(1,-2) un ángulo de 60º.
9 ) Si |u|=5 y ( u + v )·( u - v )=-10 , halla |v|.
10 ) Sabiendo que |u|=2 , |v|=6 , u y v son perpendicualares. Hallar:
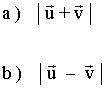
11 ) Calcular las coordenadas de cierto vector u, sabiendo que forma un ángulo de 60º con v ( 1 , 2 ) y que los módulos de ambos son iguales.
12 ) Sabiendo que:
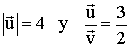
Calular u·v
13 ) Sabiendo que |u|= 3 y u = - 5v. Calular u·v
14 ) Dados los vectores u ( 3 , 1 ) y v ( 2 , -1 ). Calcular la proyección de u sobre v y la de v sobre u.
15 ) Determina un vector u que forme con v ( -2 , -4 ) un ángulo de 30º y tal que |a|=√2|b|
16 ) Dado el vector libre u ( 5 , 3 ). Calcular el vector libre v que tiene la misma dirección que u, distinto sentido y módulo igual a la unidad.
![]()
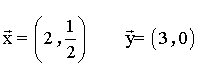
![]()
![]()
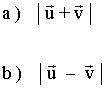
![]()
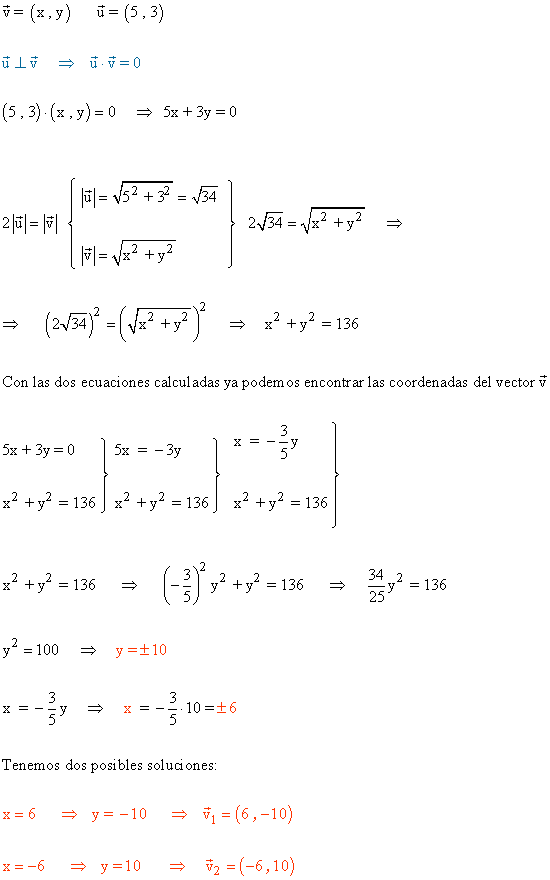

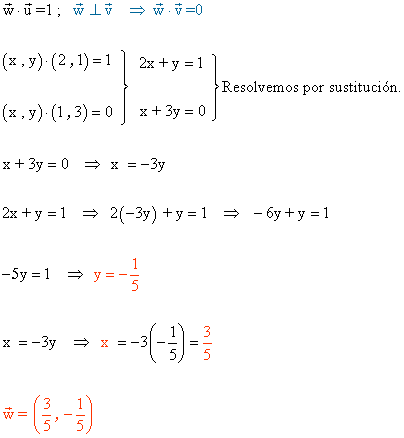
![]()
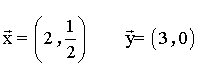
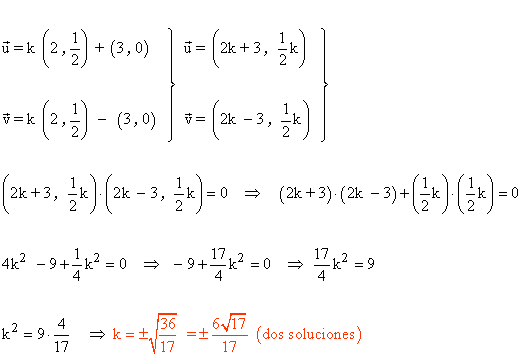
![]()
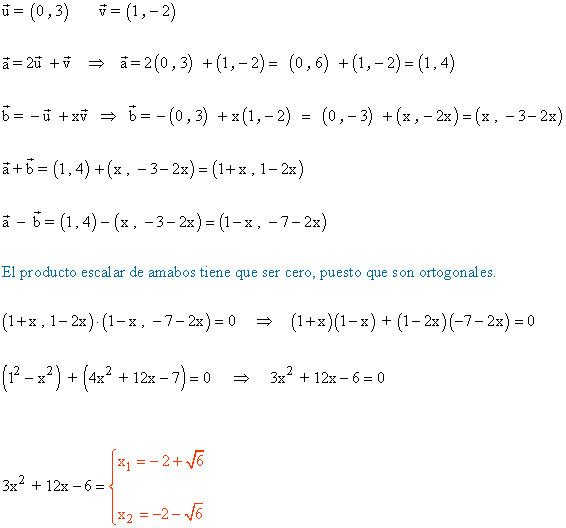
![]()

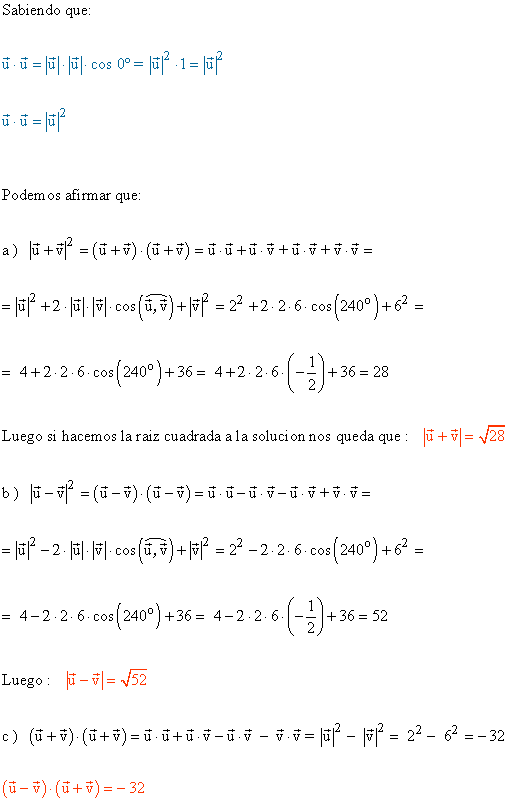
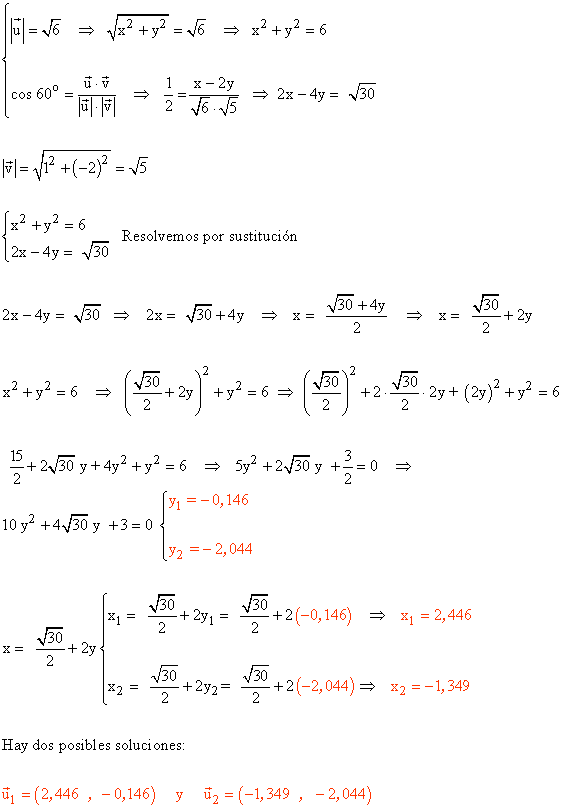
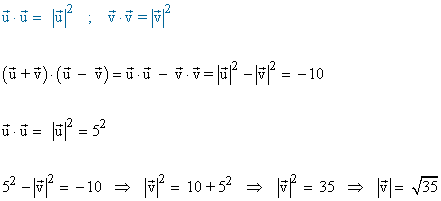
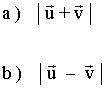
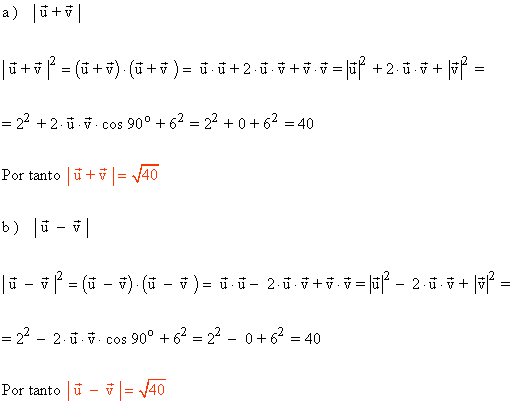
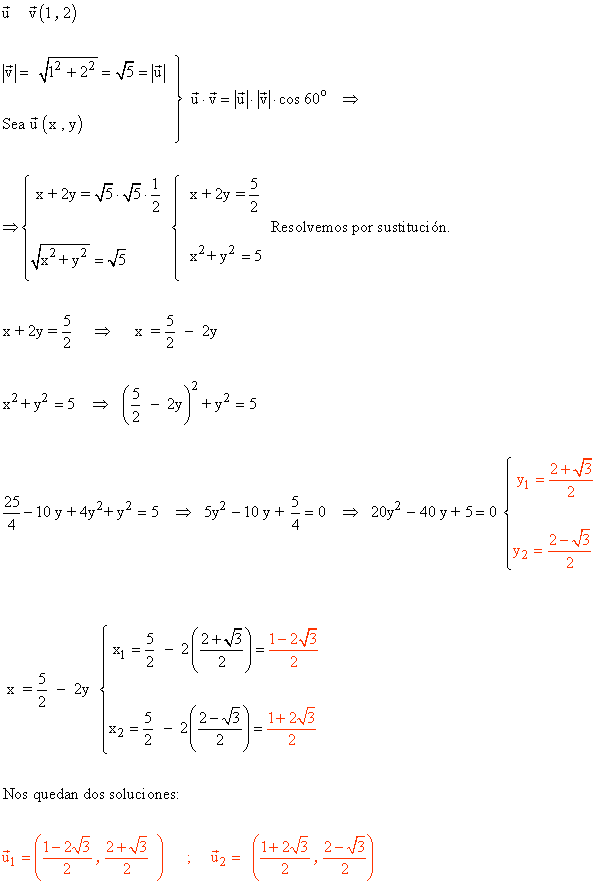
![]()
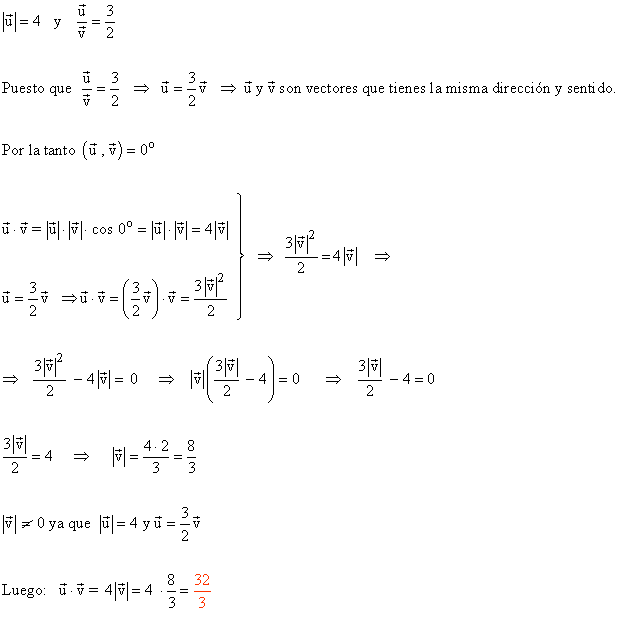
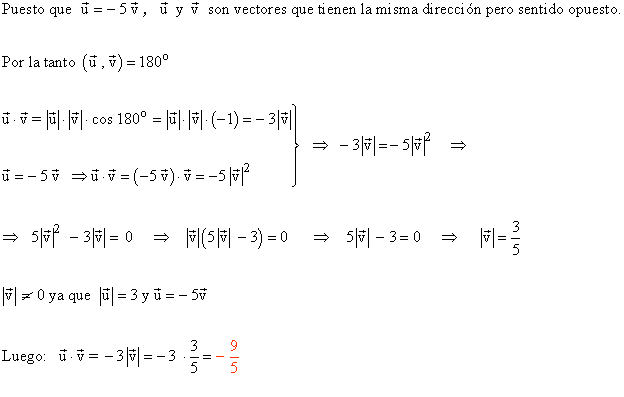
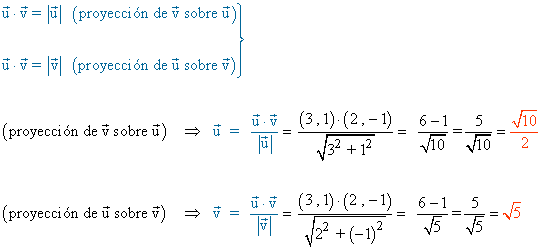
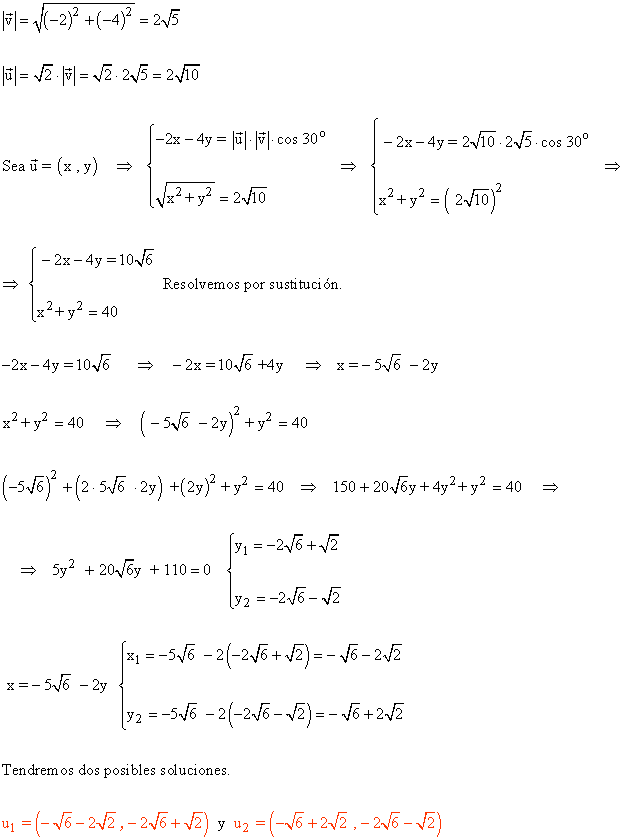



 INICIO
INICIO