Ejercicios resueltos de combinación lineal de vectores y base de un vector
1 - a ) Comprobar que el vector u(3, 9) es combinación lineal del vector v(1, 3).
1 - b ) Comprobar que el vector u(2, 3) no es combinación lineal del vector v(-1, 5).
1 - c ) Comprobar que el vector w(4, 7) es combinación lineal de los vectores u(2, 1) y v(0, 5).
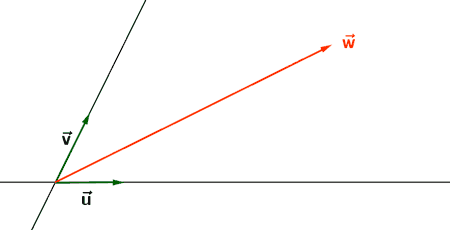
2 ) Expresar el vector w como combinación lineal de u y v de forma gráfica.
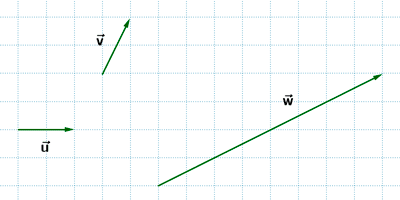
3 ) Escribe los vectores w y z como combinación lineal de los vectores u y v.
![]()
4 ) Dados los vectores u (-1,2), v (0,-3) y w (4,2), calcular x e y de modo que w = x·u + y·v (w combinación lineal de u y v)
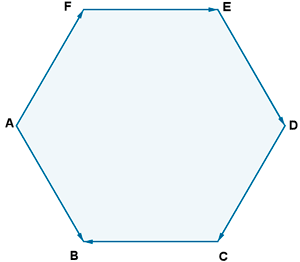
5 ) Sean A, B, C, D, E y F los vértices del hexágono regular de la figura. Expresa los vectores de los lados como combinación lineal de los vectores AB y AF.
6 ) Dado los siguientes vectores:
![]()
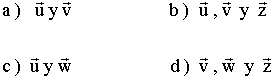
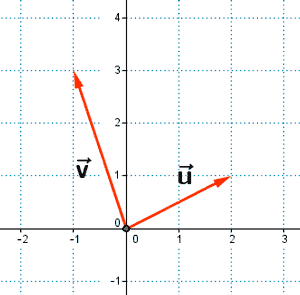
7 ) ¿Cuáles de los siguientes pares de vectores forman una base?

8 ) Dado los siguientes vectores:
![]()
9-a ) Sea u el vector de coordenadas ( 3 , -4 ) respecto a la base {( 1 , 1 ) , ( 5 , 7 )} del plano. Calcula las coordenadas de u respecto a la base canónica {( 1 , 0 ) , ( 0 , 1 )}.
9-b ) Sabemos que el vector u de coordenadas ( 2 , -3 ) respecto a la base {( 1 , 2 ) , ( 1 , 1 )} del plano. Calcula las coordenadas de u respecto de la base canónica.
10-a ) En una base ortonormal las coordenadas de un vector v son (- 2, 1). Halla las coordenadas de v en la base B {(-1,0),(0,-1)}
10-b ) En cierta base las coordenadas de un vector v son (1, -3). Halla las coordenadas de v en la base B {(1,-1),(0,-1)}
11 ) Escribe las coordenadas de los vectores representados en la siguiente imagen con respecto a la base B (u, v).
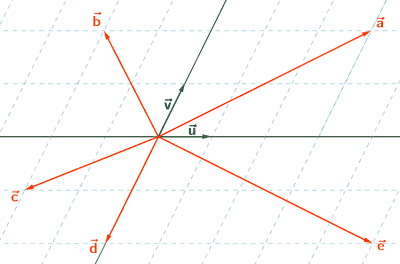
12 ) Escribe las coordenadas de los vectores representados en la siguiente imagen con respecto a la base B (u, v).
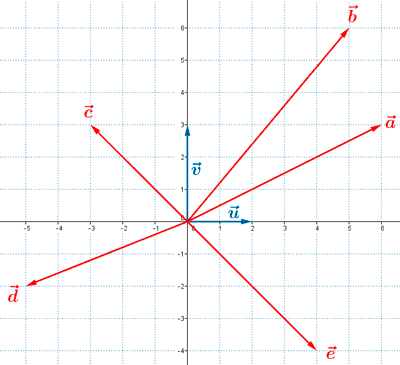
13 ) Escribe las coordenadas de los vectores representados en la siguiente imagen con respecto a la base B (i, j).
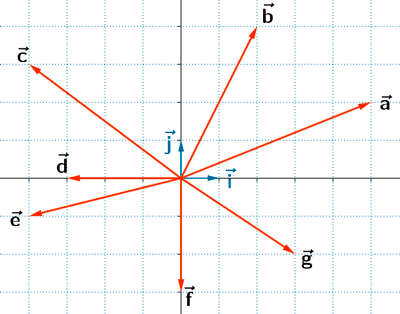
14 ) Hallar el vector v tal que w = 2 u + v , siendo:
![]()
15 ) Hallar las coordenadas de un vector v tal que w = 3 u - 1/5 v , siendo:
![]()
1 - a ) Comprobar que el vector u(3, 9) es combinación lineal del vector v(1, 3).

1 - b ) Comprobar que el vector u(2, 3) no es combinación lineal del vector v(-1, 5).

1 - c ) Comprobar que el vector w(4, 7) es combinación lineal de los vectores u(2, 1) y v(0, 5).
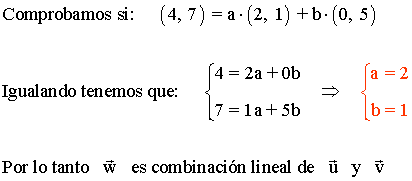
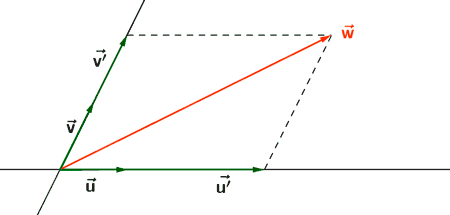
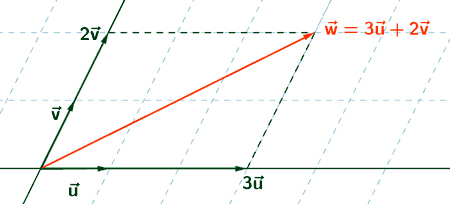
2 ) Expresar el vector w como combinación lineal de u y v de forma gráfica.

Forma gráfica:



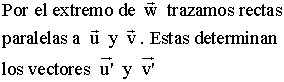
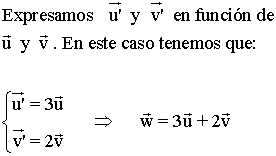
3 ) Escribe los vectores w y z como combinación lineal de los vectores u y v.
![]()
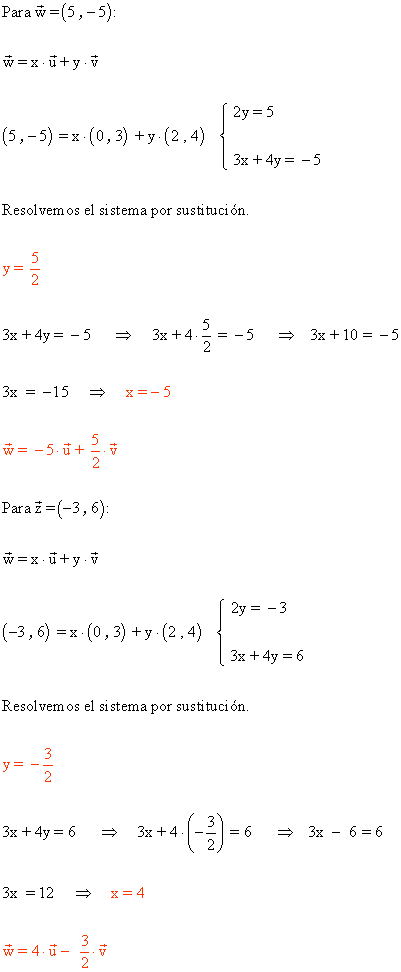
4 ) Dados los vectores u (-1,2), v (0,-3) y w (4,2), calcular x e y de modo que w = x·u + y·v (w combinación lineal de u y v)
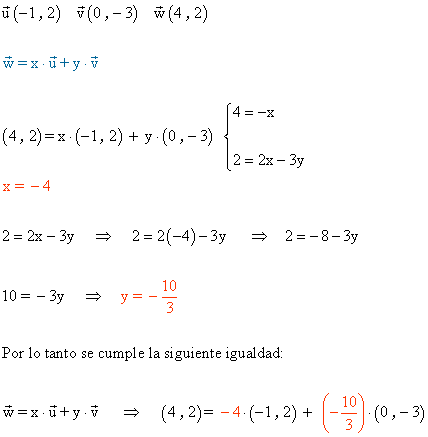
5 ) Sean A, B, C, D, E y F los vértices del hexágono regular de la figura. Expresa los vectores de los lados como combinación lineal de los vectores AB y AF.

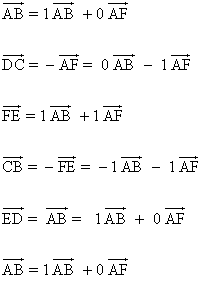
6 ) Dado los siguientes vectores:
![]()
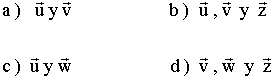

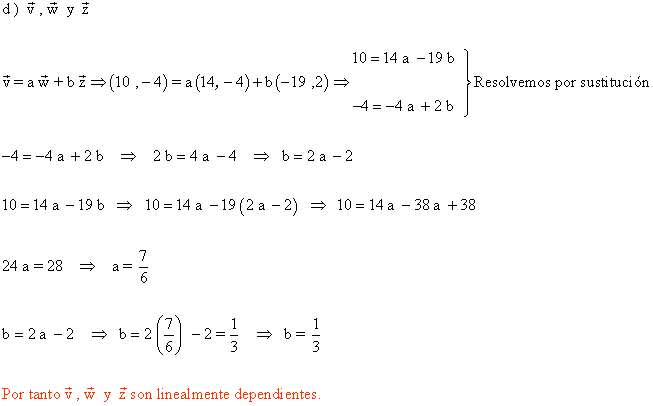
7 ) ¿Cuáles de los siguientes pares de vectores forman una base?

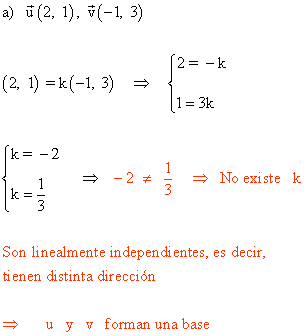
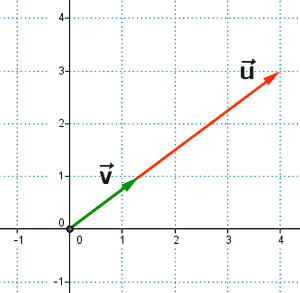
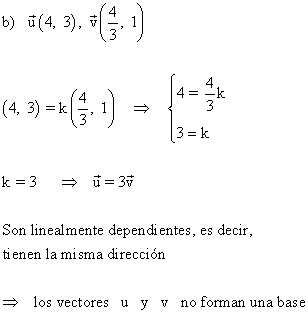
8 ) Dado los siguientes vectores:
![]()

9-a ) Sea u el vector de coordenadas ( 3 , -4 ) respecto a la base {( 1 , 1 ) , ( 5 , 7 )} del plano. Calcula las coordenadas de u respecto a la base canónica {( 1 , 0 ) , ( 0 , 1 )}.
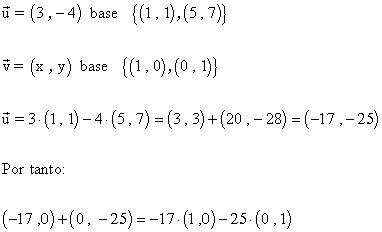
9-b ) Sabemos que el vector u de coordenadas ( 2 , -3 ) respecto a la base {( 1 , 2 ) , ( 1 , 1 )} del plano. Calcula las coordenadas de u respecto de la base canónica.
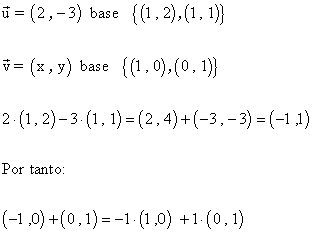
10-a ) En una base ortonormal las coordenadas de un vector v son (- 2, 1). Halla las coordenadas de v en la base B {(-1,0),(0,-1)}
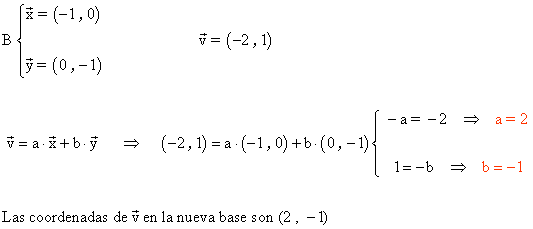
10-b ) En cierta base las coordenadas de un vector v son (1, -3). Halla las coordenadas de v en la base B {(1,-1),(0,-1)}
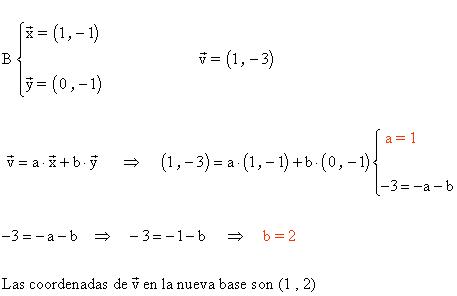
11 ) Escribe las coordenadas de los vectores representados en la siguiente imagen con respecto a la base B (u, v).

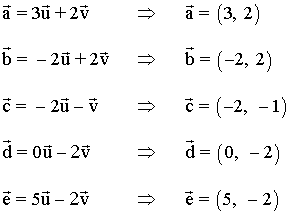
12 ) Escribe las coordenadas de los vectores representados en la siguiente imagen con respecto a la base B (u, v).

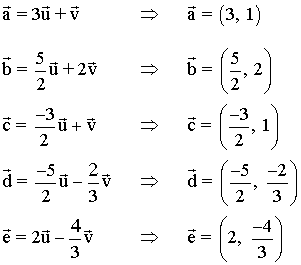
13 ) Escribe las coordenadas de los vectores representados en la siguiente imagen con respecto a la base B (i, j).

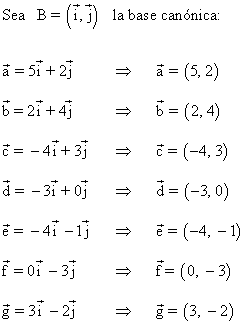
14 ) Hallar el vector v tal que w = 2 u + v , siendo:
![]()
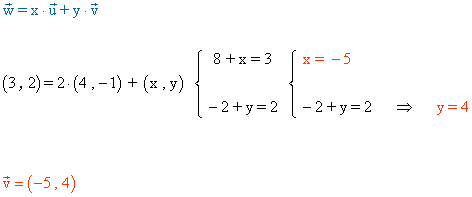
15 ) Hallar las coordenadas de un vector v tal que w = 3 u - 1/5 v , siendo:
![]()
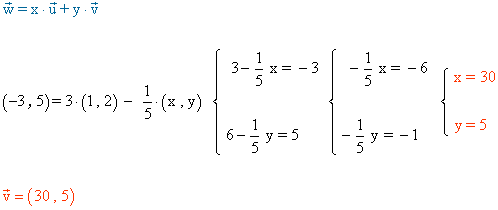


 INICIO
INICIO