Ejercicios resueltos de producto escalar de vectores
1 ) Halla el producto escalar de los siguientes vectores.

2 ) Calcula el ángulo que forman los vectores siguientes.

3-a ) Halla el valor de x para que los siguientes vectores sean perpendiculares.
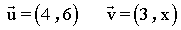
3-b ) Halla el valor de x de forma que el producto escalar de los siguientes vectores sea igual a 2.
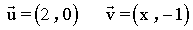
4 ) Escribe las coordenadas de dos vectores perpendiculares al siguiente vector:
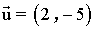
5 ) Halla un vector de módulo 1 y que sea ortogonal al siguiente vector:
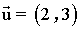
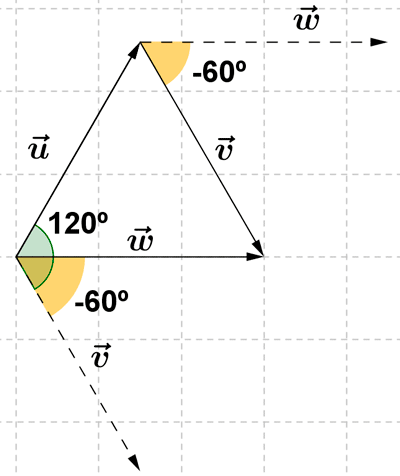
6 ) Dado los vectores de la figura,
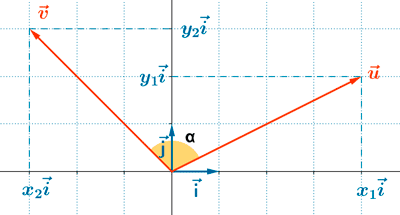
a ) Determina las coordenadas de u y v respecto de la base canónica.
b ) Halla |u|,|v| y |u + v|
c ) Halla u·v
d ) Halla la proyección de u sobre v.
e ) Calcula el ángulo que forman los vectores u y v.
f ) Encuentra un vector unitario que tenga la dirección y el sentido del vector u
g ) Halla un vector ortogonal a u y módulo unitario.
h ) Calcular un vector unitario en la dirección de v y sentido opuesto.
7 ) Dado los siguientes vectores:
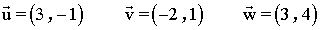
a ) Halla |u|,|v| y |w|
b ) El coseno del ángulo que forman dos a dos.
c ) Los ángulos que forman dos a dos.
d ) w + v + u analítica y graficamente.
e ) Un vector normal a w.
f ) 3v
g ) Un vector paralelo a v.
8-a ) Sean los vectores:
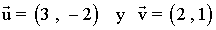
Calcula x e y de manera que ambos vectores sean perpendiculares y |v|=10
8-b ) Dado los vectores:
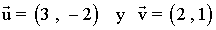
Hallar un vector w de manera que se verifique w·u=1 y w sea perpendicular a v
9 ) Calcula el valor de x para que el ángulo que forman los siguientes vectores
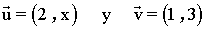
sea:
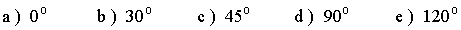
10 ) Calcula el valor de x para que el siguiente vector
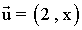
sea ortogonal al vector:
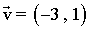
Calculado el valor de x:
a ) Hallar el módulo de u y v.
b ) Hallar el ángulo formado por los vectores u y v.
11 ) Dado el siguiente vector:
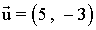
Determinar:
a ) Los vectores unitarios (módulo 1) de la misma dirección que u.
b ) Los vectores ortogonales a u que tengan el mismo módulo que u.
c ) Los vectores unitarios y ortoganales a u.
12 ) En el triángulo equilatero de la figura de 5 cm de lado, se consideran los siguientes vectores:
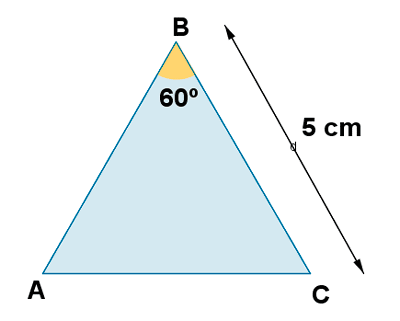
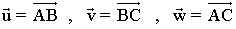
Halla u·v , v·w y w·u
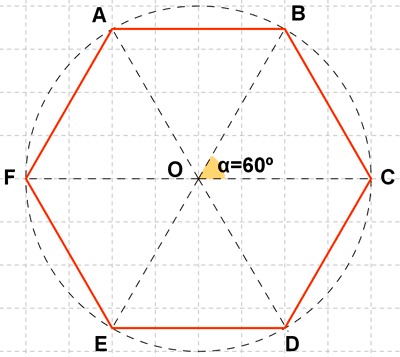
13 ) En una circunferencia de centro O y de radio 7 cm, se inscribe un hexágono regular de vértices A ,B , C D , E , F. Calcula los siguientes productos:

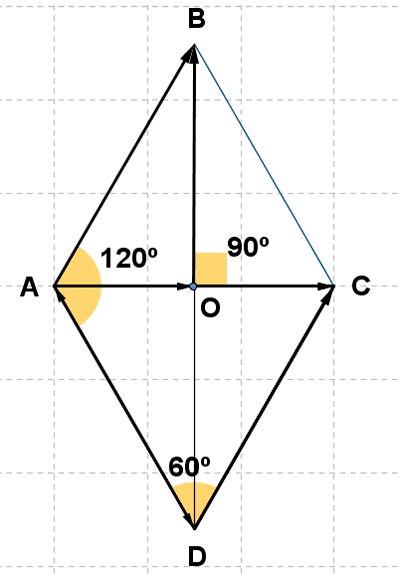
14 ) La figura ABCD rd un rombo de 4 cm y ángulos 60º y 120º hallar:
15 ) De una base B { u , v } se sabe que |u| = 2 , |v| = 3 y u·v = 3.
Sean x=(2 , -2) e y=(2,3) las coordenadas de dos vectores en esa base. Calcular x·y
16 ) Simplifica las siguientes expresiones:
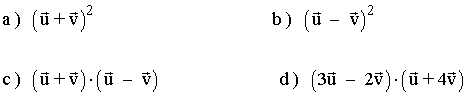
1 ) Halla el producto escalar de los siguientes vectores.

2 ) Calcula el ángulo que forman los vectores siguientes.

3-a ) Halla el valor de x para que los siguientes vectores sean perpendiculares.
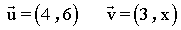
3-b ) Halla el valor de x de forma que el producto escalar de los siguientes vectores sea igual a 2.
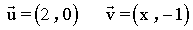
4 ) Escribe las coordenadas de dos vectores perpendiculares al siguiente vector:
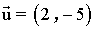
5 ) Halla un vector de módulo 1 y que sea ortogonal al siguiente vector:
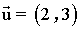
6 ) Dado los vectores de la figura,

a ) Determina las coordenadas de u y v respecto de la base canónica.
b ) Halla |u|,|v| y |u + v|
c ) Halla u·v
d ) Halla la proyección de u sobre v.
e ) Calcula el ángulo que forman los vectores u y v.
f ) Encuentra un vector unitario que tenga la dirección y el sentido del vector u
g ) Halla un vector ortogonal a u y módulo unitario.
h ) Calcular un vector unitario en la dirección de v y sentido opuesto.
7 ) Dado los siguientes vectores:
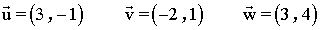
a ) Halla |u|,|v| y |w|
b ) El coseno del ángulo que forman dos a dos.
c ) Los ángulos que forman dos a dos.
d ) w + v + u analítica y graficamente.
e ) Un vector normal a w.
f ) 3v
g ) Un vector paralelo a v.
8-a ) Sean los vectores:
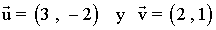
Calcula x e y de manera que ambos vectores sean perpendiculares y |v|=10
8-b ) Dado los vectores:
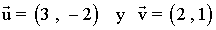
Hallar un vector w de manera que se verifique w·u=1 y w sea perpendicular a v
9 ) Calcula el valor de x para que el ángulo que forman los siguientes vectores
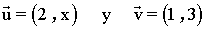
sea:
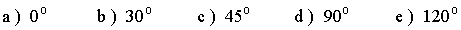
10 ) Calcula el valor de x para que el siguiente vector
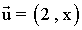
sea ortogonal al vector:
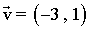
Calculado el valor de x:
a ) Hallar el módulo de u y v.
b ) Hallar el ángulo formado por los vectores u y v.
11 ) Dado el siguiente vector:
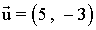
Determinar:
a ) Los vectores unitarios (módulo 1) de la misma dirección que u.
b ) Los vectores ortogonales a u que tengan el mismo módulo que u.
c ) Los vectores unitarios y ortoganales a u.
12 ) En el triángulo equilatero de la figura de 5 cm de lado, se consideran los siguientes vectores:

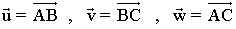
Halla u·v , v·w y w·u
13 ) En una circunferencia de centro O y de radio 7 cm, se inscribe un hexágono regular de vértices A ,B , C D , E , F. Calcula los siguientes productos:

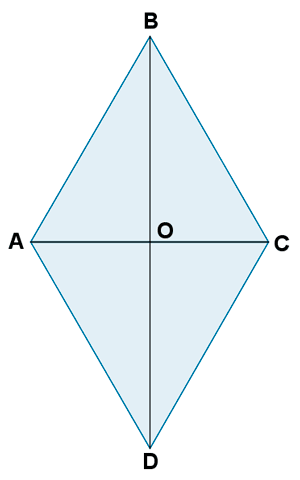
14 ) La figura ABCD rd un rombo de 4 cm y ángulos 60º y 120º hallar:
15 ) De una base B { u , v } se sabe que |u| = 2 , |v| = 3 y u·v = 3.
Sean x=(2 , -2) e y=(2,3) las coordenadas de dos vectores en esa base. Calcular x·y
16 ) Simplifica las siguientes expresiones:
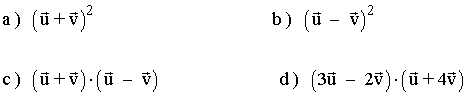
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()


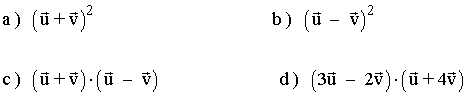
![]()
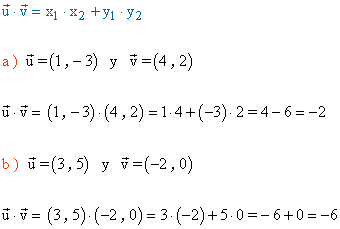
![]()
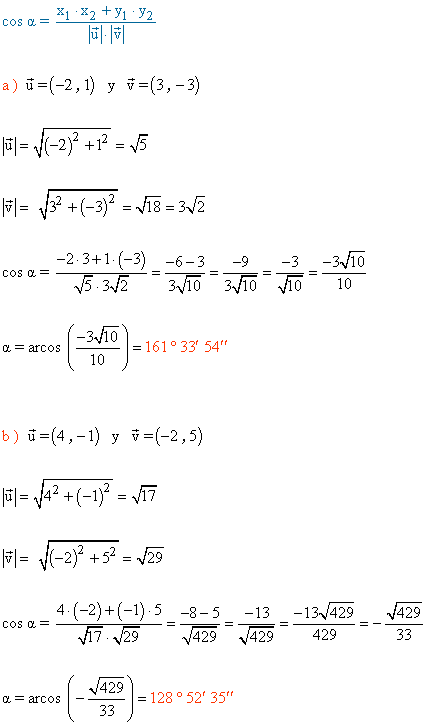
![]()
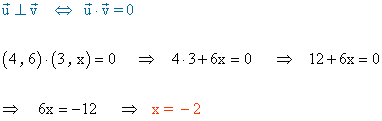
![]()
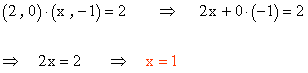
![]()
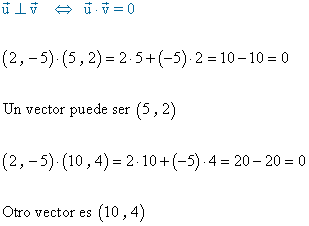
![]()


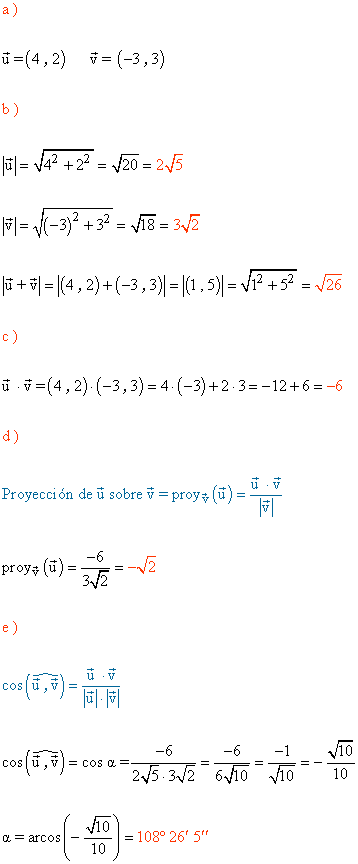
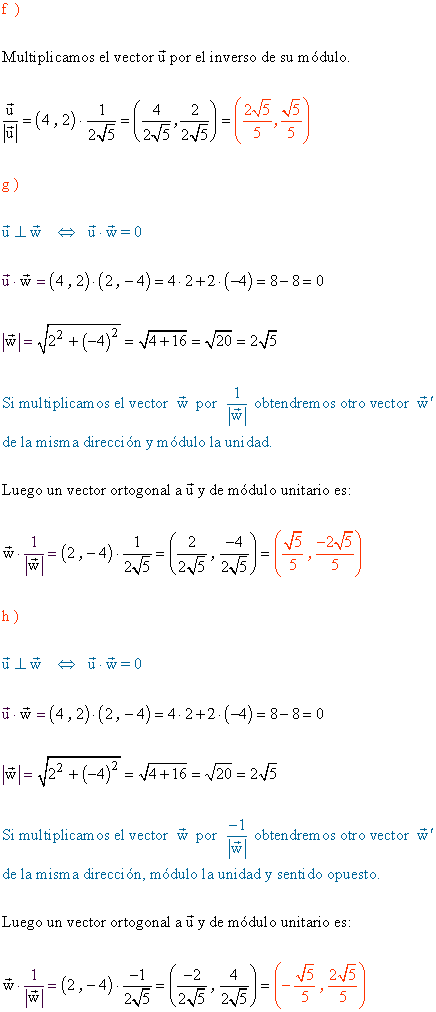
![]()

![]()
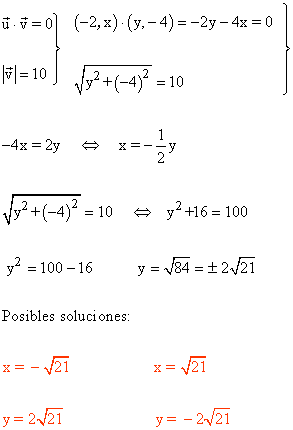
![]()
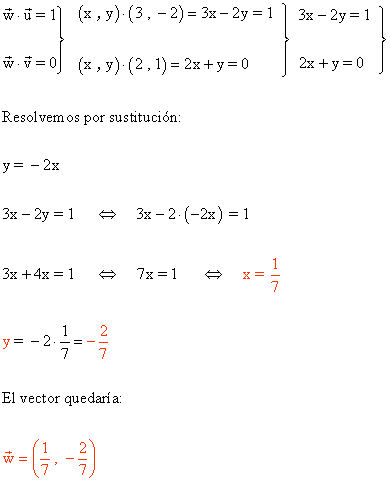
![]()
![]()
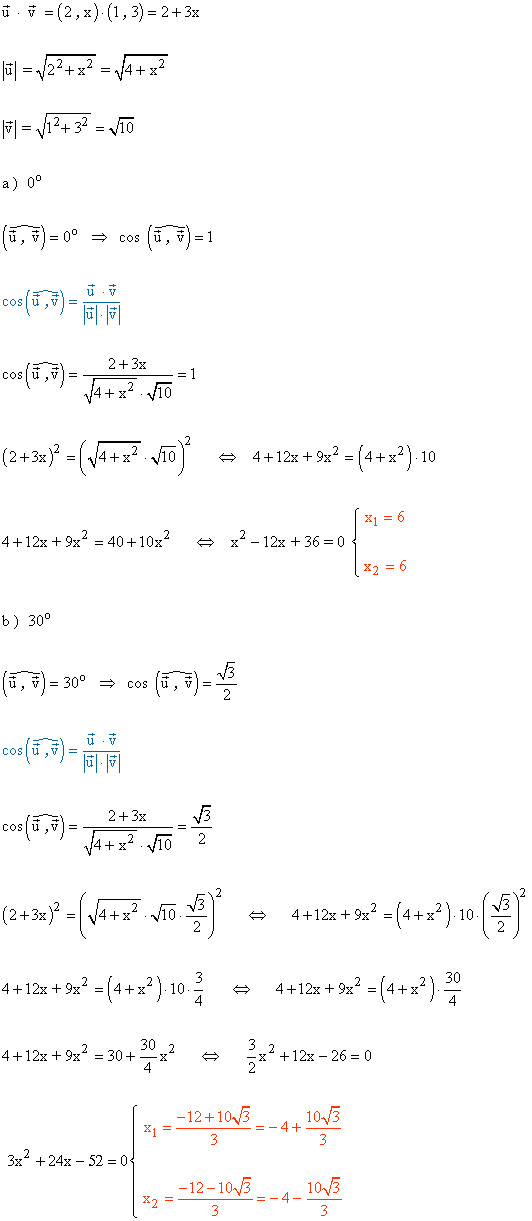
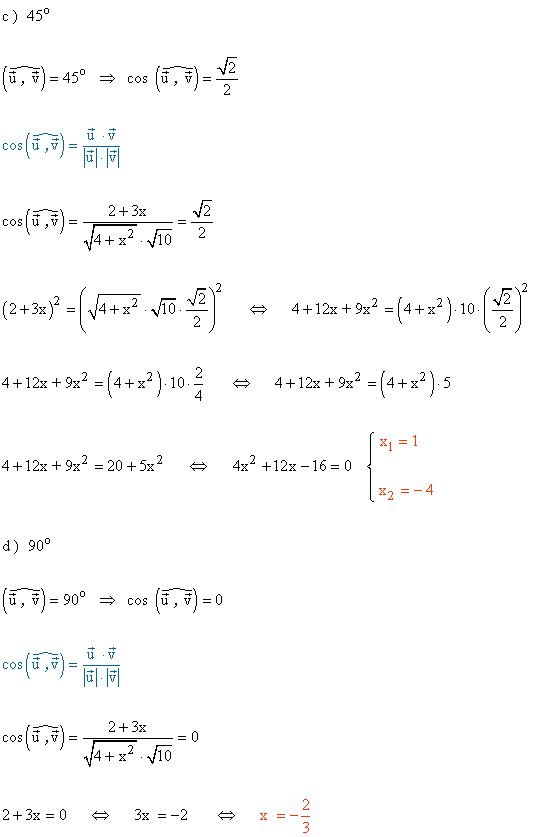
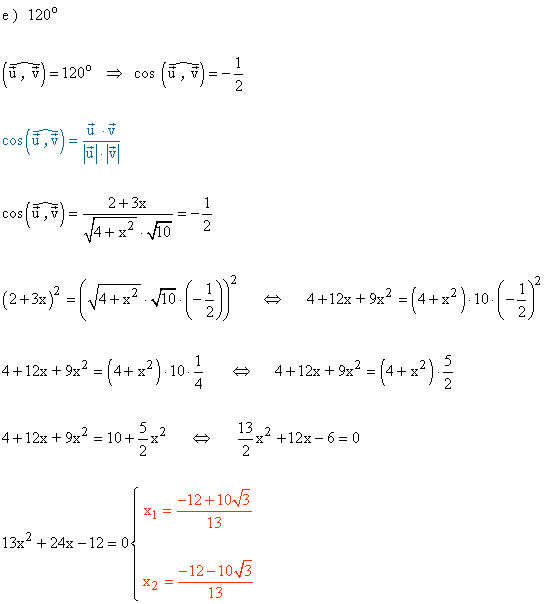
![]()
![]()

![]()

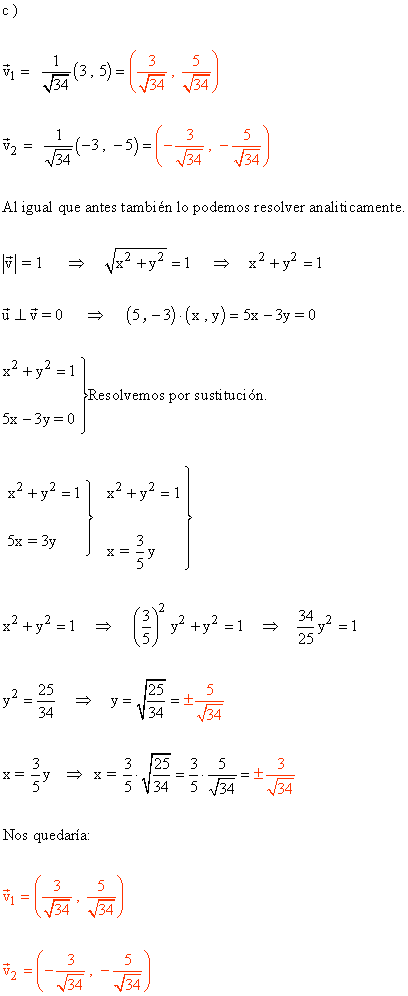

![]()
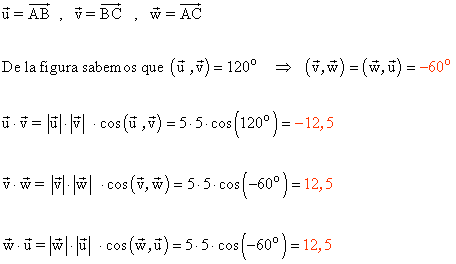






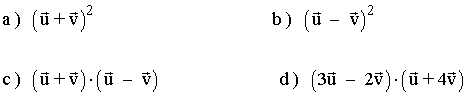
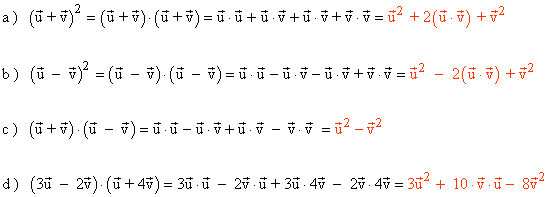


 INICIO
INICIO