Ejercicios resueltos de integrales II
Resuelve las siguientes integrales por descomposición:
![]()
![]()
![]()
![]()
![]()
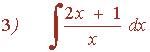
![]()
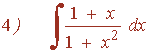
![]()
![]()
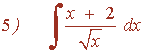
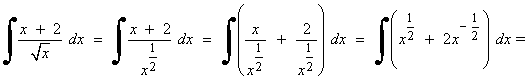
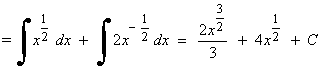
Nota de clase
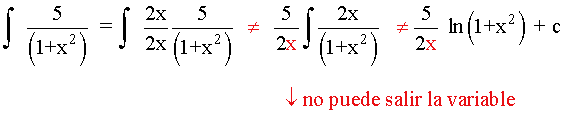
Resuelve las siguientes integrales por descomposición:
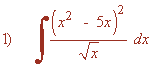
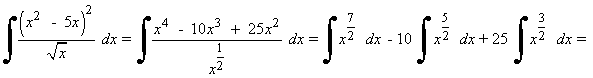
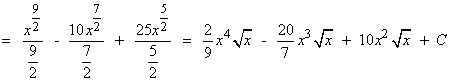
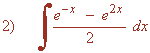
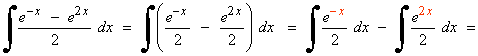
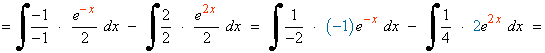
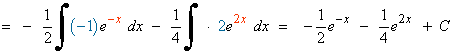
Resuelve las siguientes integrales:
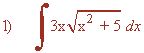
Observamos que la derivada del argumento de la raíz es u=x2+5 es u'=2x , buscaremos tener la derivada del radicando dentro de la integral para aplicar directamente la regla de la potencia.
Ver tabla de integrales inmediatas.
Como la derivada que buscamos es 2x , multiplicamos por:
![]()
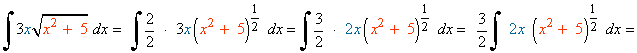
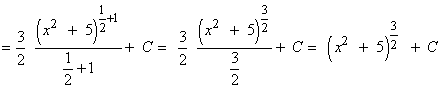
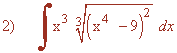
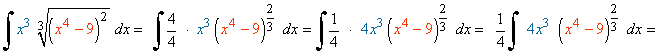
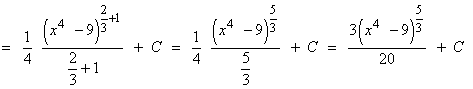
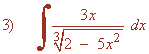
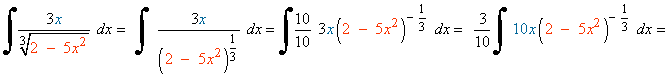
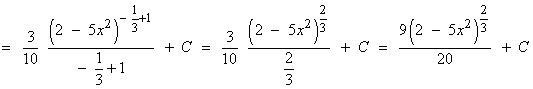
Resuelve las siguientes integrales:

Observamos que la derivada del exponente u = 2sen x es u'= 2cos x , buscaremos tener dicha derivada dentro de la integral para aplicar directamente la regla de la exponencial.
Ver tabla de integrales inmediatas.
Como la derivada que buscamos es 2cos x , multiplicamos por:
![]()
![]()
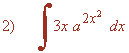
La derivada del exponente u = 2x2 es u'= 4x , buscaremos tener dicha derivada dentro de la integral para aplicar directamente la regla de la exponencial. Para ello multiplicamos por:
![]()
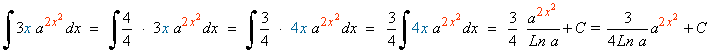
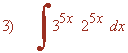
En primer lugar multiplicamos las bases, ya que tienen igual exponente. Después integramos:
![]()
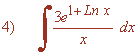
La derivada del exponente u = 1+Ln x es u'= 1/x . Como ya tenemos u' dentro de la integral, podemos integrar directamente aplicando la regla de la exponencial
![]()
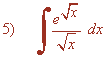
La derivada del exponente es:
![]()
Buscaremos tener dicha derivada dentro de la integral para aplicar directamente la regla de la exponencial. Para ello multiplicamos por:
![]()
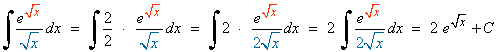
![]()
Esta integral es de la forma logarítmica.
![]()
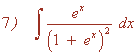
Esta integral es de la forma potencial.
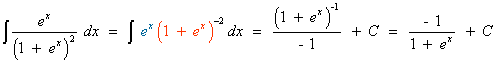
![]()
Esta integral es de la forma arcotangente.
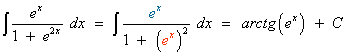
Resuelve las siguientes integrales:
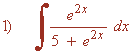
Observamos que la derivada del denominador u = 5+e2x es u'= 2e2x , buscaremos tener dicha derivada dentro de la integral para aplicar directamente la regla para el logaritmo neperiano.
Ver tabla de integrales inmediatas.
Como la derivada que buscamos es 2e2x , multiplicamos por:
![]()
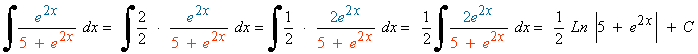
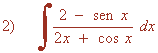
La derivada del denominador u = 2x + cos x es u'= 2 - sen x , por tanto, podemos aplicar directamente la regla para el logaritmo neperiano.
![]()
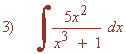
La derivada del denominador u = x3 + 1 es u'= 3x2. Multiplicamos por:
![]()
![]()
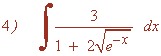
Multiplicamos numerador y denominador por: √(ex)
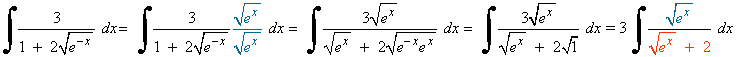
Observamos que:
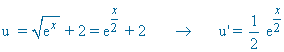
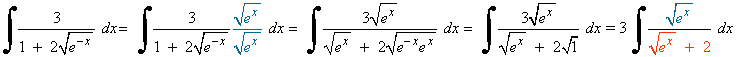
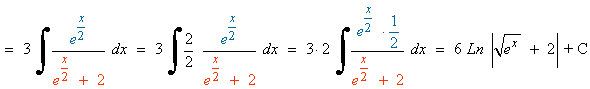


 INICIO
INICIO