Ejercicios de derivadas III
Cálculo de derivadas con literales:
En estas ecuaciones las incógnitas se representan con las letras x , y , z .
Mientras que las letras a , b , c , m , n se utilizan como constantes y las llamamos literales.
1) y = ax3 + bx - c
y ' = 3ax2 + b - 0 = 3ax2 + b
2) y = Ln(ax2 + bx + c)
![]()
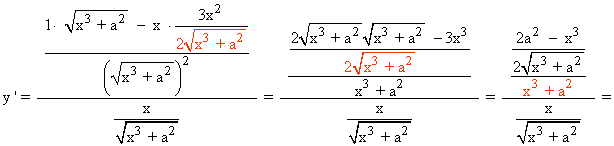
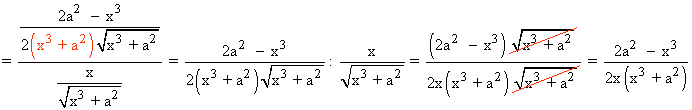
También podríamos haberlo hecho aplicando primero las propiedades de los logaritmos, y derivándola después:
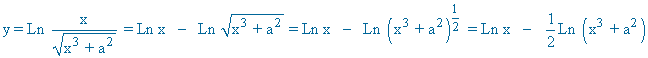
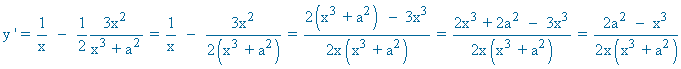
Deriva las siguientes funciones escritas en forma implícita:
1) y2 - 2x2 + 6xy - 4x = 5
Derivamos con respecto a x en ambos lados de la igualdad, teniendo en cuenta que y es función de x :
2y y ' - 4x + 6y + 6x y ' - 4 = 0
2y y ' - 4x + 6y + 6x y ' - 4= 0
Simplificamos la ecuación dividiendo cada coeficiente entre 2 :
y y ' - 2x + 3y + 3x y ' - 2= 0
Despejamos y ' :
![]()
![]()
2) x4 + 3y3 - cos x + 2xy = 2x
Derivamos con respecto a x en ambos lados de la igualdad, teniendo en cuenta que y es función de x :
4x3 + 9y y ' - (- sen x) + 2y + 2xy ' = 2
4x3 + 9y y ' + sen x + 2y + 2xy ' = 2
Despejamos y ' :
![]()
![]()
3) sen(xy) + cos(xy) = x3
Derivamos con respecto a x en ambos lados de la igualdad, teniendo en cuenta que y es función de x :
(y + xy ')·cos (xy) + (y + xy ')·(- sen xy ) = 3x2
Despejamos y ' :
(y + xy ')·cos (xy) - (y + xy ')·sen xy = 3x2
(y + xy ') ( cos xy - sen xy) = 3x2
![]()
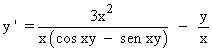
Dada la ecuación y4 - 3x3 + 2y3x2 - 5 = 0 , hallar y ' en el punto (0, 4√5).
Calculamos la derivada respecto a x del primer miembro, teniendo en cuenta que y es función de x, y empleando la Regla de la Cadena para diferenciar las funciones de y.
![]()
![]()
![]()
Despejamos y ' de la igualdad obtenida:
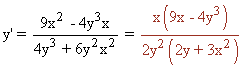
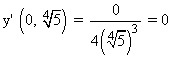
Dada la ecuación 9x2 + 4y2 = 16 , hallar y ' para x = 0 , y = 2 .
Derivamos con respecto a x en ambos lados de la igualdad, teniendo en cuenta que y es función de x :
18x + 8y y ' = 0
Despejamos y ' :
![]()
Evaluamos y ' en el punto (0 , 2) :
![]()
Calcular las diferenciales de las siguientes funciones:
1) y = ax3 + bx - c
dy = (3ax2 + b - 0) dx = (3ax2 + b) dx
![]()
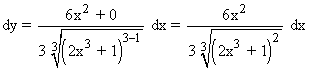
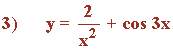
![]()
![]()
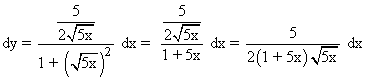
![]()
Aplicamos la propiedad de los logaritmos sobre el exponente:
![]()
Calculamos su diferencial:
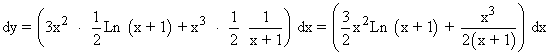


 INICIO
INICIO