Operaciones con números reales
Suma
Dados a, b y c tres números reales, se tienen las siguientes propiedades:
Operación interna: a + b = c
La suma de dos números reales cualesquiera es siempre un número real.
√5+π+3 es un número real.
Asociativa: ( a + b ) + c =a + ( b + c )
El orden de agrupación de los sumandos no altera el resultado.
(3+√2)+√8=3+(√2+√8)
Conmutativa: a + b = b + a
El orden de los sumandos no altera la suma.
√3+1,4=1,4+√3
Elemento nulo: a + 0 = a
El elemento neutro o elemento nulo en la suma es el cero, pues es el número que, sumado a cualquier otro número real, da como resultado el mismo número.
Φ+0=Φ
Elemento opuesto: a + ( -a ) = 0
El elemento simétrico de la suma también se llama elemento opuesto. Los números reales a y -a son opuestos el uno del otro.
Dos números reales son simétricos si al sumarlos dan como resultado el elemento neutro.
√2 + ( -√2 ) = 0, el elemento opuesto de √2 es -√2.
( -5 ) + 5 = 0, el elemento opuesto de -5 es 5.
Producto
Dados a, b y c tres números reales, se tienen las siguientes propiedades:
Operación interna: a · b= c
El producto de dos números reales cualesquiera es siempre un número real.
π·√2 es un número real.
Asociativa: ( a · b ) · c = a · ( b · c )
El orden de agrupación de los factores no altera el resultado.
( √2 · √3 ) · π = √2 · (√3 · π )
Conmutativa: a · b = b · a
El orden de los factores no altera el producto.
Φ · 3/2 = 3/2 · Φ
Elemento unidad: a · 1 = a
El elemento neutro o elemento unidad en el producto es el uno, pues es el número que, al multiplicarlo por cualquier otro número real, da como resultado dicho número.
√2 · 1 = √2
Elemento inverso: 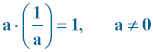
El elemento simétrico del producto también se llama elemento inverso. Los números reales a y 1/a son inversos el uno del otro.
Dos números reales son simétricos si al multiplicarlos dan como resultado el elemento neutro.
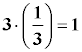
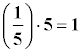
El inverso de una fracción:
![]()
![]()
El inverso del inverso es el mismo número:
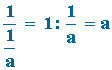
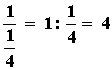
Distributiva respecto de la suma: a · ( b + c ) = a · b + a · c
El producto de un número por una suma es igual a la suma de los productos de dicho número por cada uno de los sumandos.
π · ( √2 + 4 ) = π · √2 + π · 4
Reglas de los signos
(+) · (+) = (+) ( +a ) ( +b ) = + ab 3 · y = 3y
( + ) · ( - ) = ( - ) ( +a ) ( -b ) = -ab 3 · ( -y )= - 3y
( - ) · ( + ) = ( - ) ( -a ) ( +b ) = -ab ( -3 ) · x = - 3x
( - ) · ( - ) = ( + ) ( -a ) ( -b ) = ab ( -x ) · ( -y ) = xy
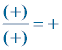
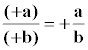
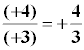
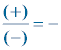
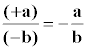
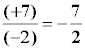
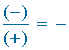

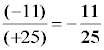
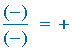
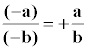
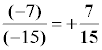


 INICIO
INICIO

