Valor absoluto
El valor absoluto de un número real a coincide con él mismo si es positivo ó 0, y es igual a su opuesto si es negativo. Se representa por |a|. 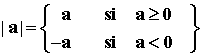
De modo que el valor absoluto de cualquier número nunca es negativo.
El valor absoluto de un número coincide siempre con el de su opuesto.
Ejemplos de valor absoluto
a) |3,5| = 3,5
b) |-1,6| = 1,6
c) |4 - 9| = |-5| = 5
d) |π - 2| = π - 2 = 1,141...
e) |-3| + |√2| = 3 + √2 = 4,414...
f) |-4,2| - |-4,2| = 4,2 - 4,2 = 0
Propiedades del valor absoluto
1. |a| = |-a|
2. |a · b| = |a| · |b|
3. |a +b | ≤ |a| + |b| Desigualdad triangular
4. Si |a| < k -k < a < k
![]()
Ejemplos de las propiedades del valor absoluto
1. |-7| = |7| =7
2. |(-2) · 5| = |-10| = 10 = |-2| · |5| = 2 · 5
3. |4 + 2| = |6| = 6 = |4| + |2|
Igualmente:
|4 + (-2)| = |2| = 2 ≤ |4| + |-2| = 4 + 2 = 6
4. Si |3|<4, entonces -4 < 3 < 4
Observaciones de las propiedades del valor absoluto
|x| = a son los valores x tales que x = a o x = - a
|x| < a son los valores x tales que - a < x < a
|x| > a son los valores x tales que x < - a o x > a
La desigualdad |x| ≤ a describe el intervalo cerrado [-a , a] , simétrico respecto al origen.
Y los números reales |x| < a son los del intervalo abierto (-a, a).
La desigualdad |x| ≥ a describe la unión de los intervalos (-∞ , -a] ∪ [a , ∞).
Y los números reales |x| > a son la unión de los intervalos abiertos (-∞ , -a) ∪ (a , ∞).
La desigualdad |x - c| < d es el intervalo abierto (c - d , c + d) , denominado también entorno de centro c y radio d, E(c , r).
La desigualdad |x - c| ≤ d es el intervalo cerrado [c - d , c + d].
La desigualdad |x - c| > d es la unión de los intervalos (-∞ , c - d) ∪ (c + d , ∞).
La desigualdad |x - c| ≥ d es la unión de los intervalos (-∞ , c - d] ∪ [c + d , ∞).
Ejemplos de las propiedades del valor absoluto
a) La expresión |x| < 5 representa el intervalo abierto (-5, 5)
|x| < 5 ⇔ -5 < x < 5 ⇔ x ∈ (-5,5)
b) La expresión |x| ≤ 5 representa el intervalo cerrado [-5, 5]
|x| ≤ 5 ⇔ -5 ≤ x ≤ 5 ⇔ x ∈ [-5,5]
c) La expresión |x-5| ≤ 7 representa el intervalo cerrado [-2, 12]
pues |x-5| ≤ 7 ⇔ -7 ≤ x - 5 ≤ 7 ⇔ - 7 + 5 ≤ x ≤ 7 + 5 ⇔ - 2 ≤ x ≤ 12 ⇔ x ∈ [-2, 12]
d) La expresión |x| > 5 representa la unión de intervalos (-∞, -5)∪(5, ∞), pues
|x| > 5 ⇔ x < -5 o x > 5 ⇔ x ∈ (-∞ , -5) ∪ (5 , ∞)
e) La expresión |x-5| ≥ 7 representa la unión de intervalos (-∞, -2] ∪ [12 , ∞), pues
|x-5| ≥ 7 ⇔ x-5 ≤ -7 o x-5 ≥ 7 ⇔ x ≤ 5-7 o x ≥ 5+7 ⇔ x ∈ (-∞ , -2] ∪ [12 , ∞)
Expresión con valor absoluto |
Interpretación Geométrica | Expresión sin valor Absoluto |
|---|---|---|
| |x| = a | La distancia de x al origen es a | x = ± a |
 |
||
| |x| < a | La distancia de x al origen es estrictamente menor que a | - a < x < a |
 |
||
| |x| ≤ a | La distancia de x al origen es menor o igual que a | - a ≤ x ≤ a |
 |
||
| |x| > a | La distancia de x al origen es estrictamente mayor que a | x >a ó x < - a |
 |
||
| |x| ≥ a | La distancia de x al origen es mayor o igual que a | x ≥ a ó x ≤ - a |
 |
||
| 0 < |x| < a | La distancia de x al origen es estrictamente menor que a y estrictamente mayor que 0 | 0 < |x| ⇔ x≠ 0 |x| < a ⇔ - a < x < a Por tanto: 0 < |x| <a ⇔ x≠ 0 y - a < x < a |
 |
||
e < |x| < a |
La distancia de x al origen es estrictamente menor que a y estrictamente mayor que e | e < |x| ⇔ x > e ó x < - e |x| < a ⇔ - a < x < a Por tanto: 0 < |x| < a ⇔ - a < x < -e ó e < x < a |
 |
||
Distancia
La distancia entre dos números a y b es el valor absoluto de su diferencia.
d(a,b) = |b-a| = |a-b|
La distancia entre a y b es la longitud del segmento de extremos a y b . Por tanto, la distancia entre dos números siempre es positiva.
La unidad de medida de longitud es la distancia entre los números 0 y 1.
Ejemplo de distancia entre dos puntos
La distancia entre los números -4 y 7 será: d(-4,7) = |(-4) -7| = |7 - (-4)| = 11
Expresión con valor absoluto |
Interpretación Geométrica | Expresión sin valor Absoluto |
|---|---|---|
| |x - c| = d | La distancia entre x y c es d | x - c = ± d ⇔ x = d + c ó x = - d +c |
 |
||
| |x - c| < d | La distancia entre x y c es estrictamente menor que d | - d < x - c < d ⇔ - d + c < x < d + c |
 |
||
| |x - c| ≤ d | La distancia entre x y c es menor o igual que d | |
 |
- d ≤ x - c ≤ d ⇔ - d + c ≤ x ≤ d + c |
|
| |x - c| > d | La distancia entre x y c es estrictamente mayor que d | x - c > d ó x - c < - d Por tanto: x > c + d ó x < c - d |
 |
||
| |x - c| ≥ d | La distancia entre x y c es mayor o igual que d | x - c ≥ d ó x - c ≤ - d Por tanto: x ≥ c + d ó x ≤ c - d |
 |
||
| 0 < |x - c| < d | La distancia entre x y c es estrictamente menor que d y estrictamente mayor que 0 | 0 < |x - c| ⇔ x - c ≠ 0 ⇔ x ≠c |x - c| < d ⇔ - d + c < x < d + c Por tanto: 0 < |x - c| < d ⇔ x ≠c y - d + c < x < d + c |
 |
||
e < |x- c| < d |
La distancia de x al origen es estrictamente menor que d y estrictamente mayor que e | e < |x - c| ⇔ x > c + e ó x < c - e |x| < d ⇔ - d < x < d Por tanto: 0 < |x| < d ⇔ c - d < x < c - e ó c + e < x < c + d |
 |
||


 INICIO
INICIO

