Ejercicios resueltos de hipérbolas
1 ) En las siguientes hipérbolas calcular los ejes, focos, vértices y asíntotas y representa gráficamente:

2 ) En las siguientes hipérbolas calcular los ejes, focos, vértices y asíntotas y representa gráficamente:

3 ) En las siguientes hipérbolas calcular los ejes, focos, vértices y asíntotas y representa gráficamente:

4 ) Halla las ecuaciones en forma reducida de las hipérbolas de focos en el eje OX y que cumplan las siguientes condiciones:
a) Pasa por el punto (2, 0) y tiene por asíntotas y = ±3x
b) Los focos son (-3, 0) y (3, 0) y la distancia entre sus vértices 4
c) Un foco es (5, 0) y su excentricidad es 2
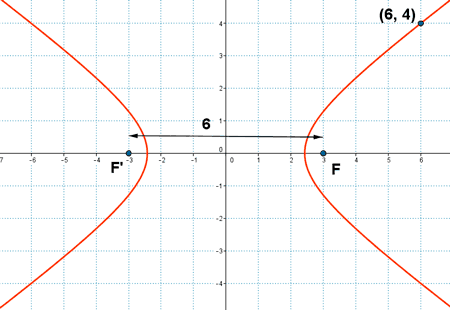
d) Pasa por el punto (6, 4) y cuyo eje focal mide 6
5 ) El foco de una hipérbola se halla a una distancia de 6 unidades de un vértice y a 14 unidades del otro. Escribe su ecuación.
6 ) Escribe la ecuación del lugar geométrico de los puntos cuya diferencia de distancias a los focos F(3, 0) y F'(-3, 0) es igual a 4 .
7 ) Escribe la ecuación del lugar geométrico de los puntos cuya diferencia de distancias a los focos F(0, 4) y F'(0, -4) es igual a 4 .
8 ) Dada la siguiente hipérbola:
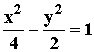
Hallar su hipérbola conjugada y representarla gráficamente.
9 ) Hallar la hipérbola equilátera cuya distancia focal es 2c = 6√2 y comprobar si el punto P(5, 4) pertenece a dicha hipérbola.
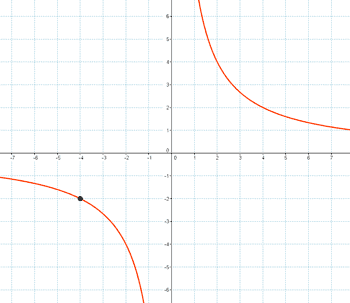
10 ) Hallar la hipérbola equilátera referida a sus asíntotas y que pasa por el punto P(-4, -2).
11 ) Dada la hipérbola 4x2 - y2 = 28 hallar las rectas tangente y la normal en el punto de ordenada y = 6 y abscisa positiva.
12 ) Hallar la hipérbola equilátera referida a sus asíntotas y que pasa por el punto P(-4, -2).
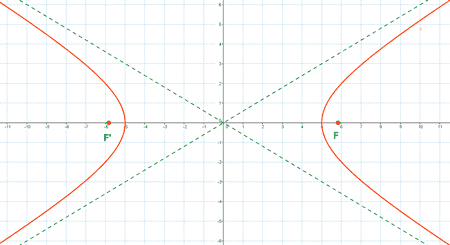
1 ) En las siguientes hipérbolas calcular los ejes, focos, vértices y asíntotas y representa gráficamente:

(a)
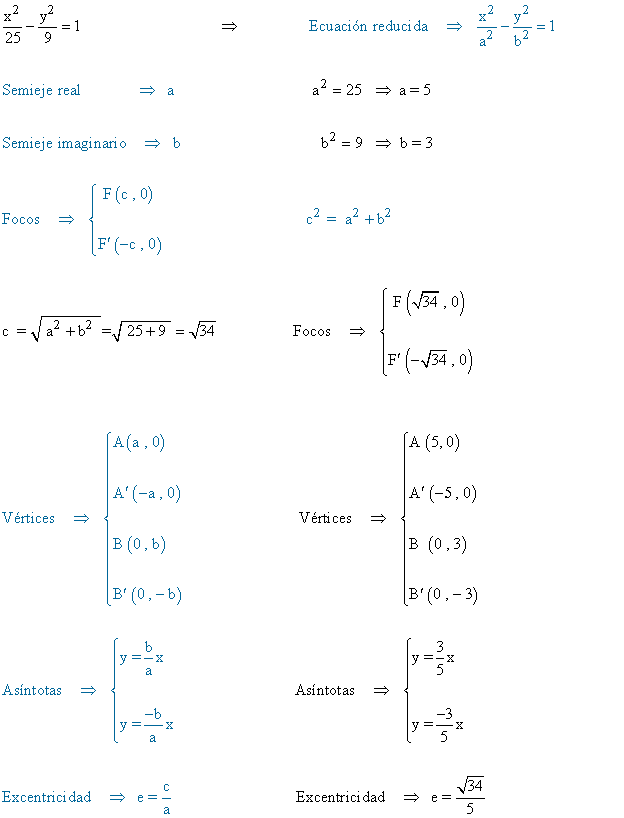
(b)
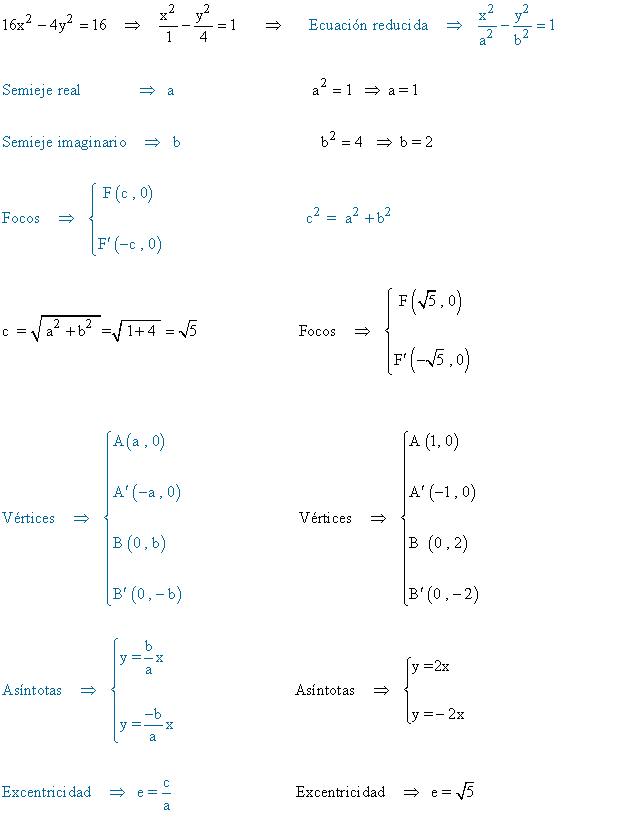
2 ) En las siguientes hipérbolas calcular los ejes, focos, vértices y asíntotas y representa gráficamente:

(a)
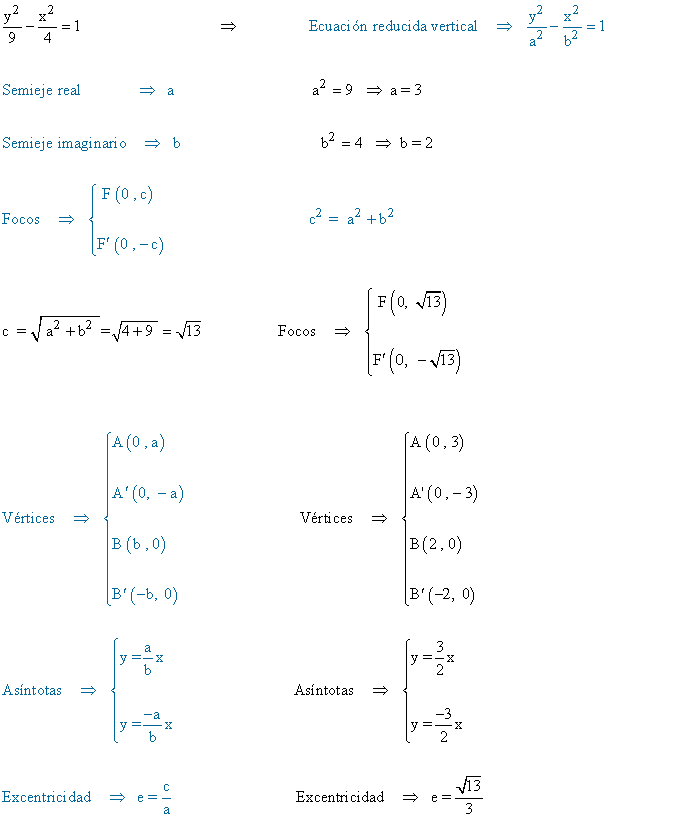
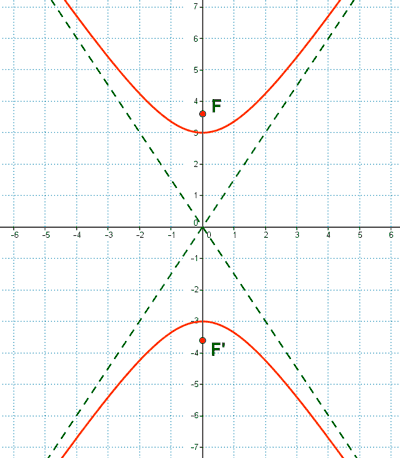
(b)
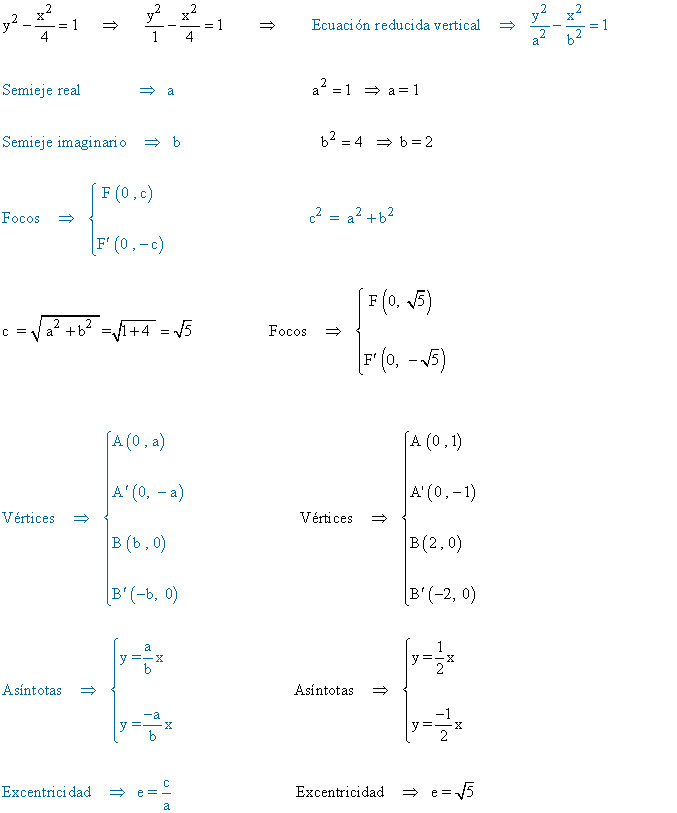
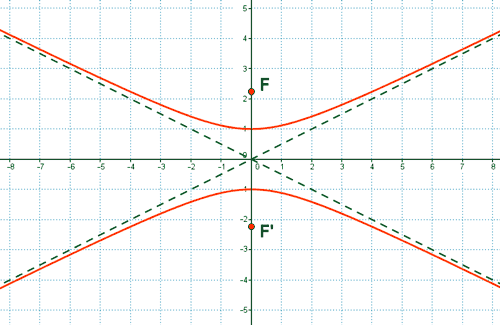
3 ) En las siguientes hipérbolas calcular los ejes, focos, vértices y asíntotas y representa gráficamente:

(a)
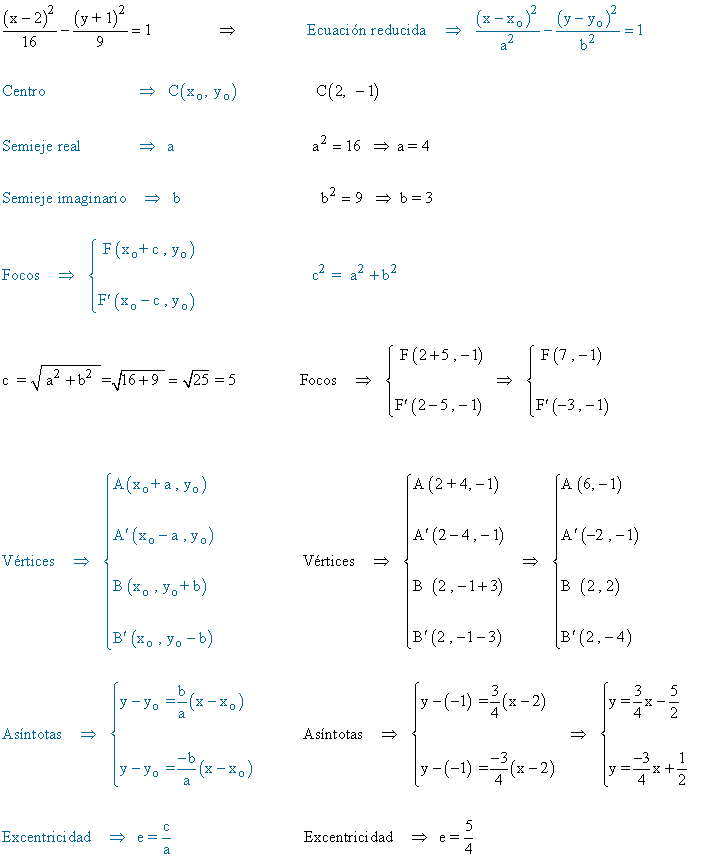
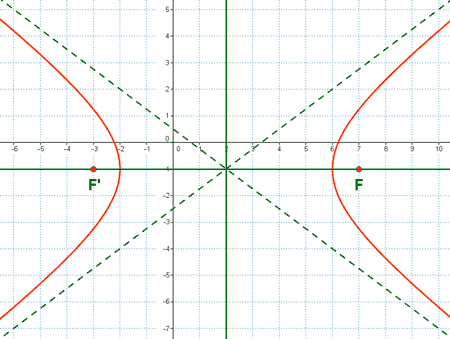
(b)
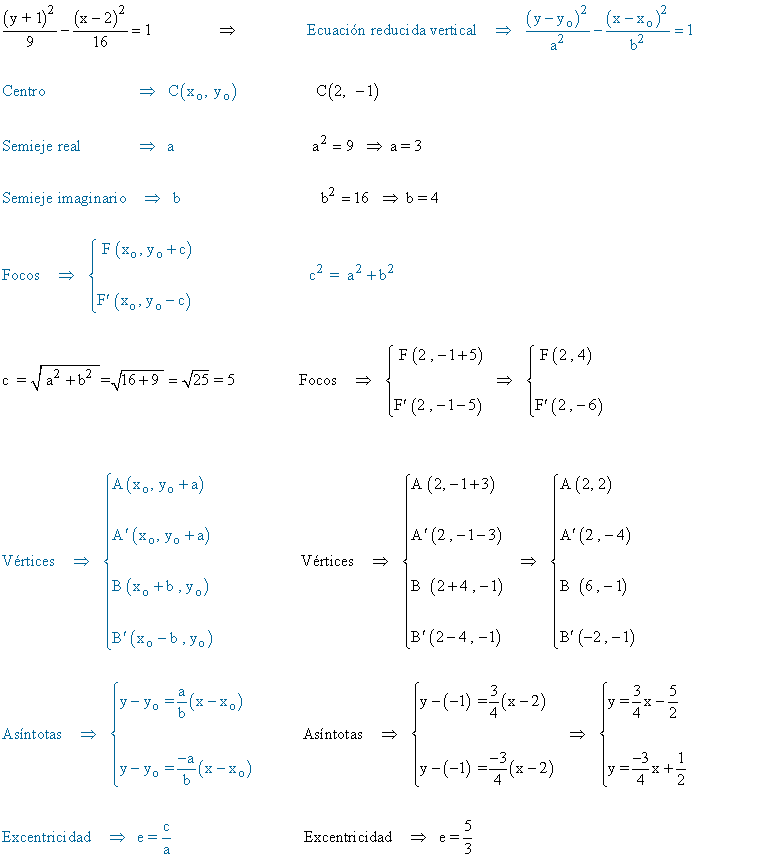
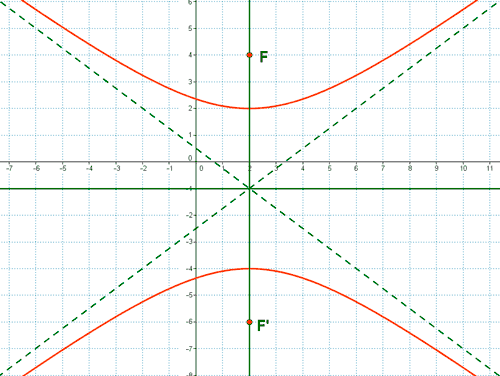
4 ) Halla las ecuaciones en forma reducida de las hipérbolas de focos en el eje OX y que cumplan las siguientes condiciones:
a) Pasa por el punto (2, 0) y tiene por asíntotas y = ±3x
b) Los focos son (-3, 0) y (3, 0) y la distancia entre sus vértices 4
c) Un foco es (5, 0) y su excentricidad es 2
d) Pasa por el punto (6, 4) y cuyo eje focal mide 6
(a)
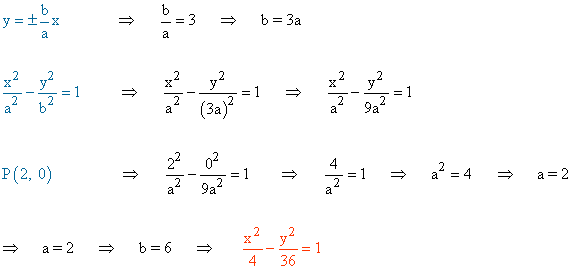
(b)
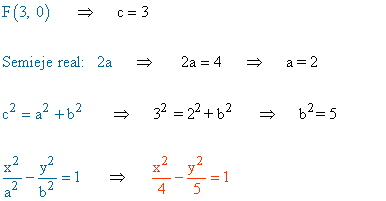
(c)
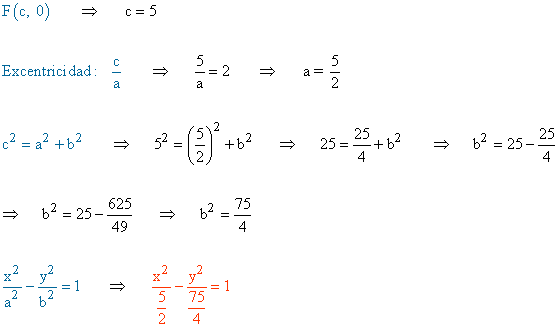
(d)
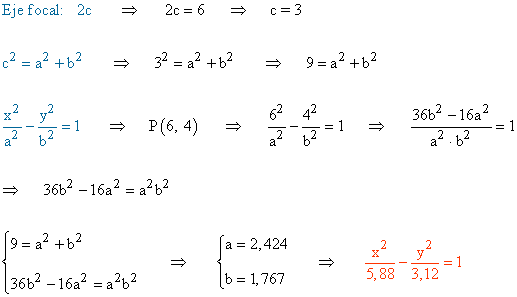
5 ) El foco de una hipérbola se halla a una distancia de 6 unidades de un vértice y a 14 unidades del otro. Escribe su ecuación.
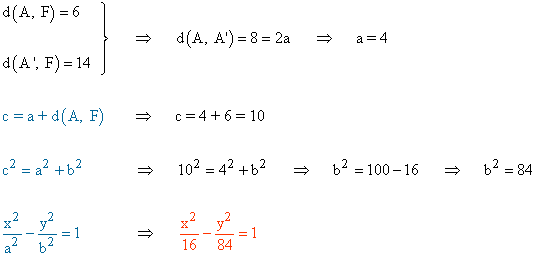
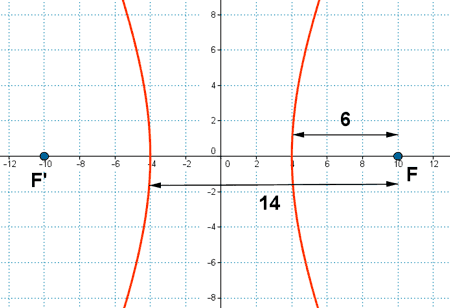
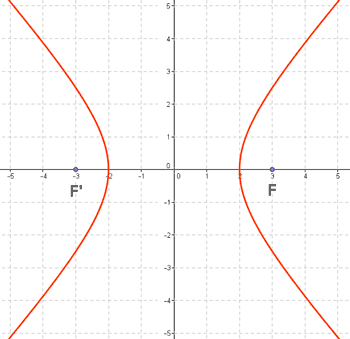
6 ) Escribe la ecuación del lugar geométrico de los puntos cuya diferencia de distancias a los focos F(3, 0) y F'(-3, 0) es igual a 4 .
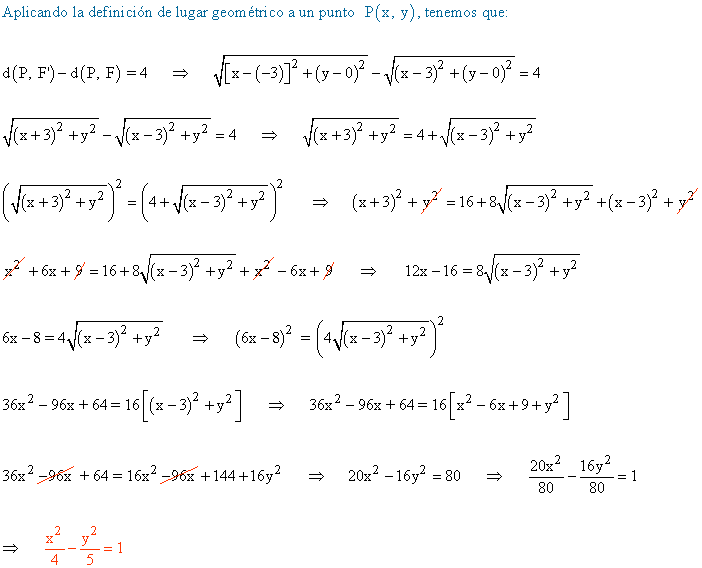
Otro método:

7 ) Escribe la ecuación del lugar geométrico de los puntos cuya diferencia de distancias a los focos F(0, 4) y F'(0, -4) es igual a 4 .
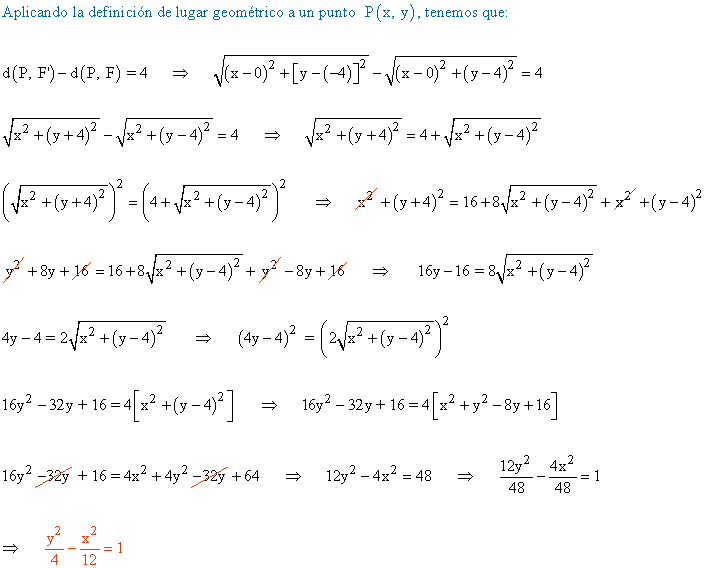
Otro método:

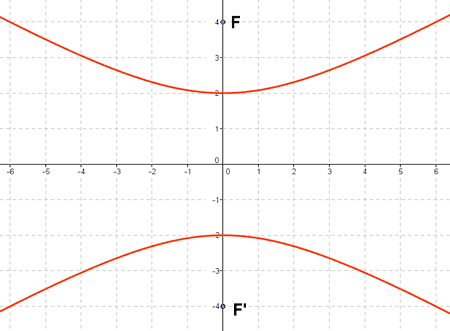
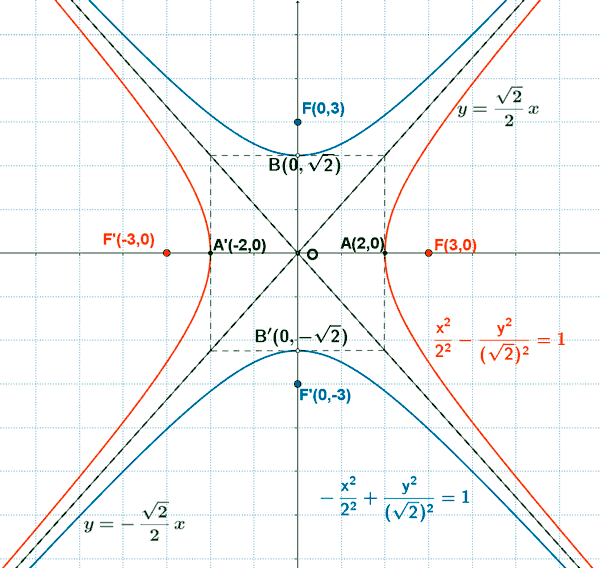
8 ) Dada la siguiente hipérbola:
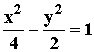
Hallar su hipérbola conjugada y representarla gráficamente.
Hipérbola original

Hipérbola conjugada
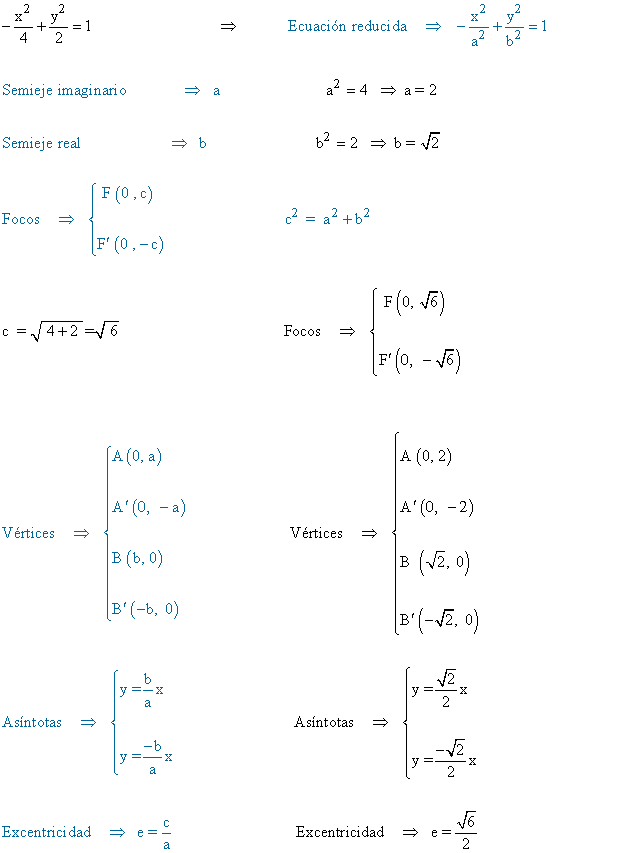
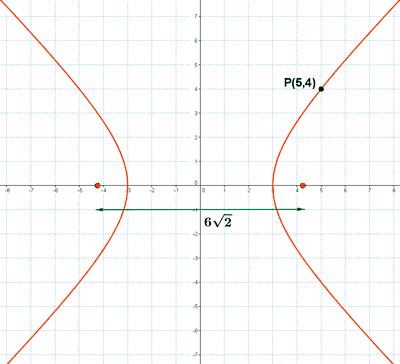
9 ) Hallar la hipérbola equilátera cuya distancia focal es 2c = 6√2 y comprobar si el punto P(5, 4) pertenece a dicha hipérbola.
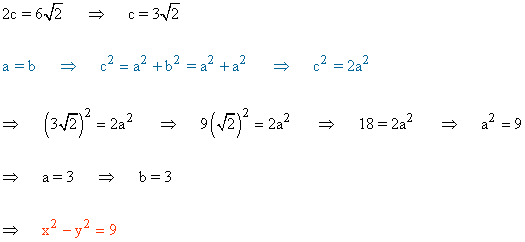
A continuación comprobamos si el punto P(5, 4) pertenece a la hipérbola:
![]()
Como satisface la ecuación, el punto pertenece a la hipérbola.
10 ) Hallar la hipérbola equilátera referida a sus asíntotas y que pasa por el punto P(-4, -2).
![]()
11 ) Dada la hipérbola 4x2 - y2 = 28 hallar las rectas tangente y la normal en el punto de ordenada y = 6 y abscisa positiva.
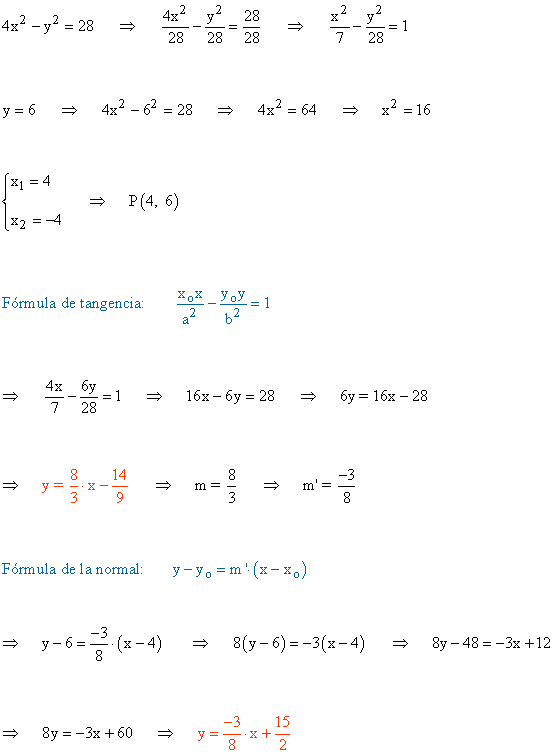
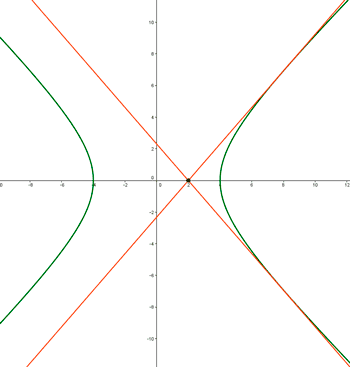
12 ) Hallar la hipérbola equilátera referida a sus asíntotas y que pasa por el punto P(-4, -2).
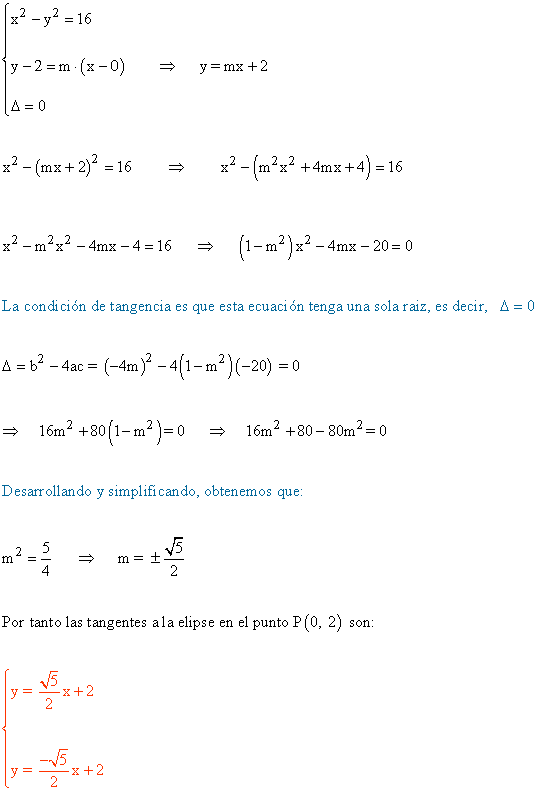


 INICIO
INICIO