Teorema del valor medio del cálculo integral
Si f es continua [a, b] existe al menos un número c∈[a, b] tal que:
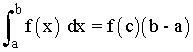
Al número f(c) se le llama valor medio de f en el intervalo [a, b]
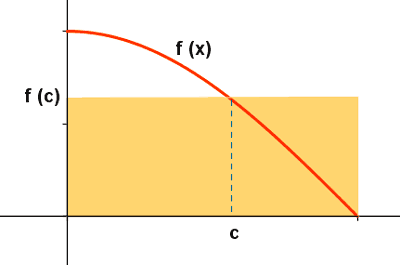
Geométricamente el teorema del valor medio establece que dada una función positiva en [a, b] el área del recinto limitado por la gráfica de la función, el eje OX y las rectas x = a y x = b coincide con el área de un rectángulo de base igual a la longitud del intervalo (b - a) y altura f(c) siendo c un punto del intervalo [a, b] .
Ejemplo:
1) Calcula el valor medio de la función f(x) = sen x entre x = 0 y x = π/2
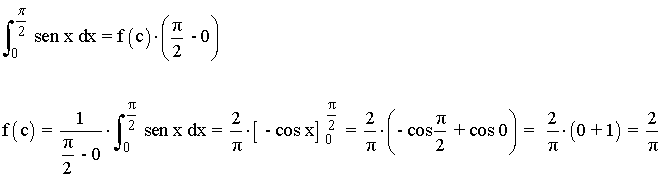
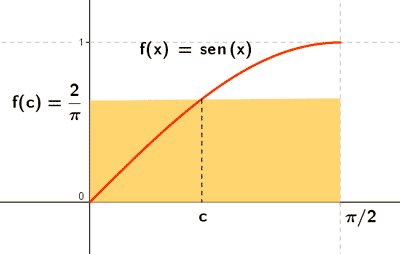
2) Dada la función f(x) = x2 + 2 para que valor c se verifica el teorema del valor medio entre x = 1 y x = 3 .
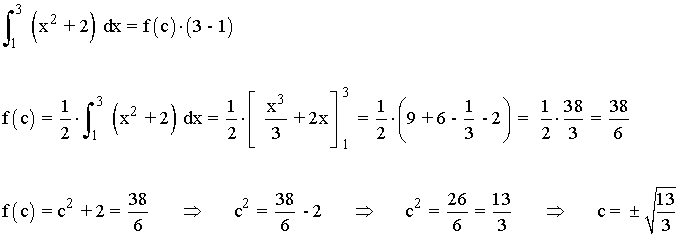
Descartamos la solución negativa puesto que el valor c debe pertenecer al intervalo [1, 3] .
3) Demostrar que existe un punto c en el intervalo [0, 3] para que la siguiente función:
![]()
cumpla el teorema del valor medio.
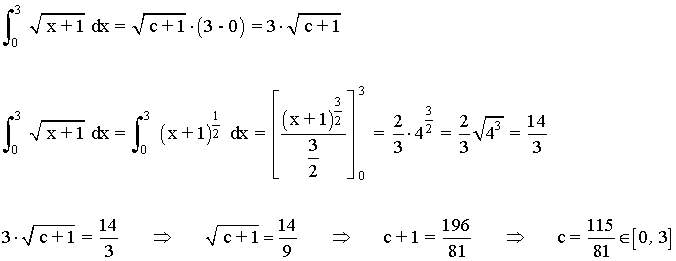


 INICIO
INICIO

