Teorema fundamental del cálculo integral
Si f es una función continua en [a, b] , y F es la función definida en [a, b] como:
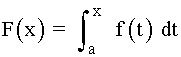
entonces F es derivable en (a, b) y F ' (x) = f(x) , para todo x∈(a, b) .
Ejemplo:
1) Calcular la derivada de la siguiente función:
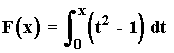
Como f(t) = t2 - 1 es una función continua, para calcular F ' (x) aplicamos el teorema fundamental del cálculo integral:
![]()
2) Calcular la derivada de la siguiente función:
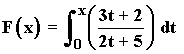
Puesto que f(t) es una función continua en el intervalo (0, +∞) aplicando el teorema fundamental del cálculo tenemos que:
![]()
Gráfico de las funciones derivables e integrables
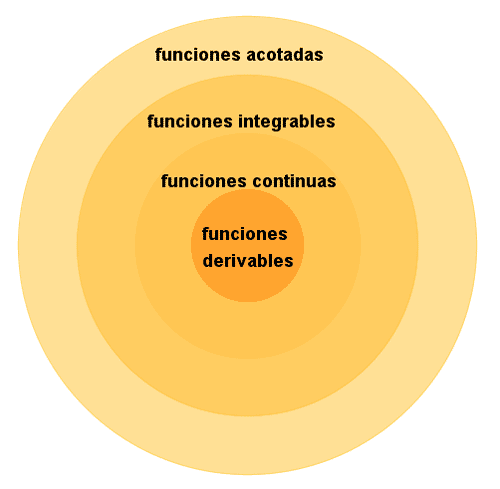


 INICIO
INICIO

