Ejercicios resueltos de comparación de infinitos.
Ejercicios resueltos de infinitésimos.
Al comparar el orden de los infinitos se distinguen tres casos:
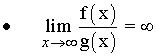
Se dice que f(x) es de orden superior a g(x).
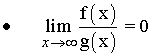
Se dice que f(x) es de orden inferior a g(x).
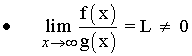
Se dice que f(x) y g(x) son del mismo orden.
Resumen de infinitésimos
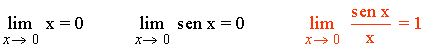
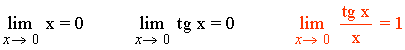
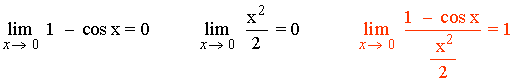
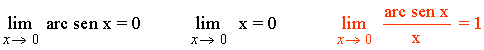
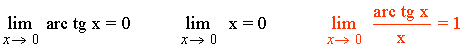
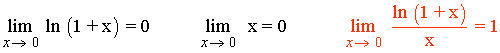
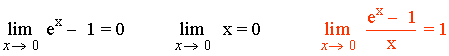
Límites que conviene conocer
No existen:
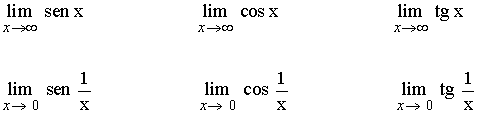
Infinitos:
![]()
Finitos:
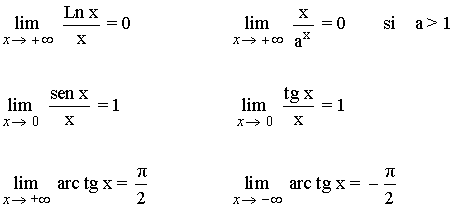
A) Ordena de menor a mayor los órdenes de los siguientes infinitos:
√x log2x x 3√x (1,5)x 2x3 5x 3x5
Solución:
log2x 3√x √x x 2x3 3x5 (1,5)x 5x
B) Por comparación de infinitos realiza de forma inmediata los siguientes límites:
1) 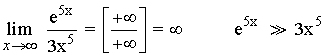
El numerador es de mayor grado que el denominador.
2) 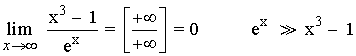
3) 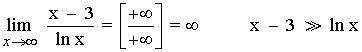
4) 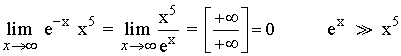
5) 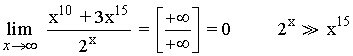
6) 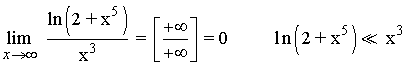
7) 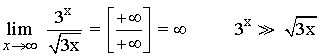
8) 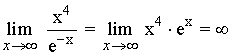
9) 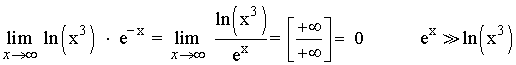
10) 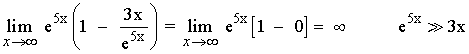
11) 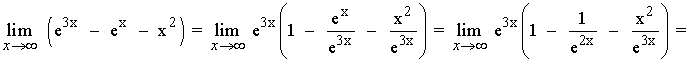
![]()
Sin operar, calcula el límite cuando x → -∞ de las siguientes expresiones:
1) ![]()
2) 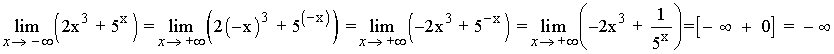
3) 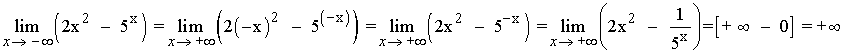
4) ![]()
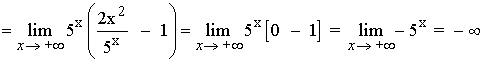
5) ![]()
6) 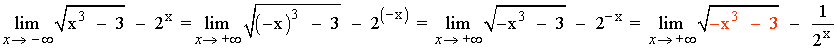
El límite no existe, ya que el argumento de la raíz cuadrada es negativo.
7) ![]()
8) ![]()
9) 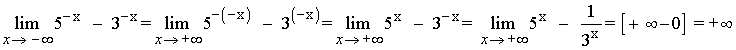
Determina el valor de los siguientes límites aplicando la equivalencia de infinitésimos:
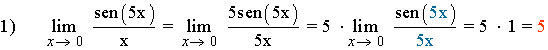
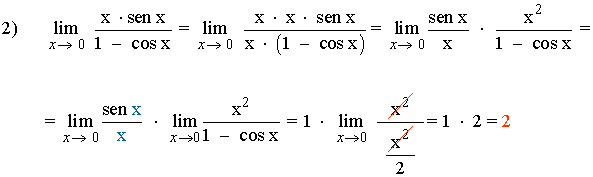
![]()
![]()
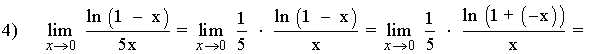
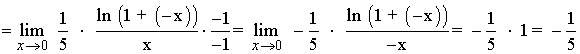
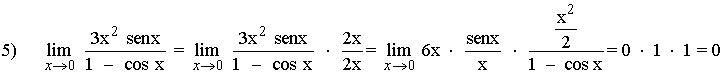
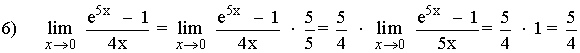
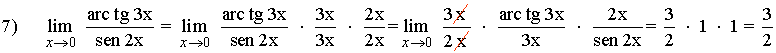


 INICIO
INICIO