Derivadas laterales
Se define la derivada por la izquierda de f(x) en el punto x = a :
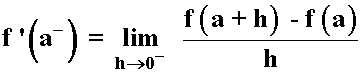
Se define la derivada por la derecha de f(x) en el punto x = a :
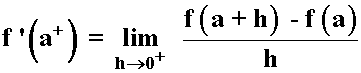
A ambas derivadas se les llama derivadas laterales.
Derivabilidad y continuidad en un punto
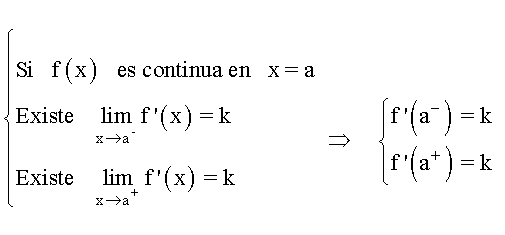
Si f(x) es derivable en x=a si es continua en x = a y existen los límites laterales de la función derivada y estos son iguales.
Derivabilidad y continuidad en un intervalo
Se dice que f(x) es derivable en un intervalo cerrado [a, b] si es derivable en (a, b) y existen además las derivadas por la derecha en x = a y por la izquierda en x = b.
Casos en que una función es continua y no es derivable
Ejemplo de una gráfica con un punto angular:
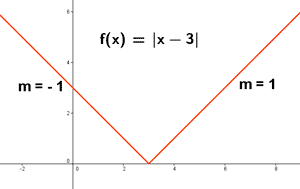
Sea la función f(x) = | x - 3 |
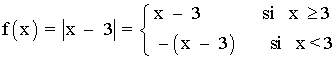
Calculamos los límites laterales en el punto x = 3 :
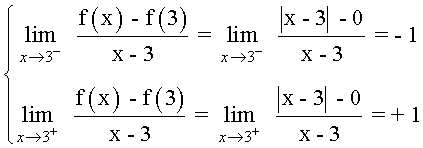
Como los límites laterales (derivada por la izquierda y derivada por la derecha no son iguales, la función f(x) no es derivable en x = 3 y la gráfica de f(x) no tiene tangente en el punto (3, 0) .
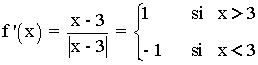
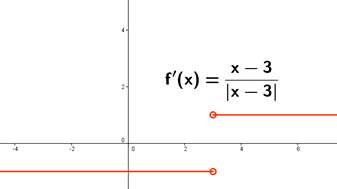
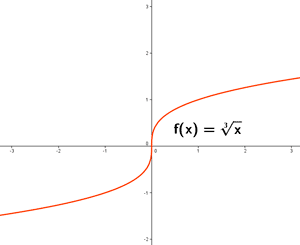
Ejemplo de una gráfica con una recta tangente vertical:
![]()
f(x) es continua en x = 0 . Sin embargo, al calcular el límite cuando x tiende a 0 , obtenemos:
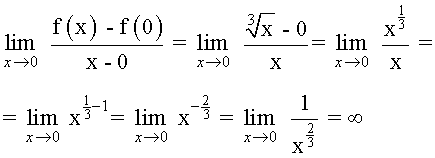
El límite de la función f(x) cuando x tiende a 0 es infinito, luego la recta tangente en x = 0 es vertical. Es decir, la función f(x) no es derivable en x = 0 .
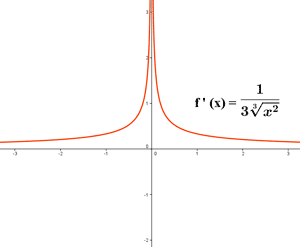
Ejemplo de una función a trozos continua y no derivable:
Dada la siguiente función:
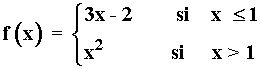
1) Comprobar que es continua en x = 1 pero no derivable.
2) Da un ejemplo de función que sea derivable y no sea continua.
1) La función será continua si y solo si se cumple que:
![]()
Como f(1) = 1 , tenemos que hallar los límites laterales:
![]()
![]()
Hemos demostrado que:
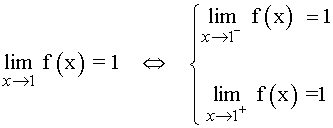
Por lo tanto la función es continua en el punto x = 1 .
Para comprobar que la función no es derivable en x = 1, hay que demostrar que no existe el siguiente límite:
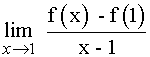
Para ello basta con probar que los límites laterales son distintos:
Límite por la izquierda
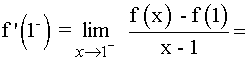
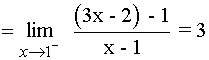
Límite por la derecha
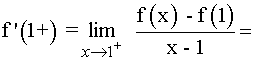
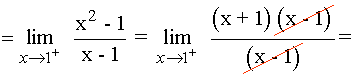
![]()
Como los límites laterales en x = 1 son distintos, la función no es derivable en dicho punto.
2) No es posible encontrar un ejemplo puesto que todas las funciones derivables son continuas.
Conclusión entre derivabilidad y continuidad:
Según los dos ejemplos anteriores una función puede ser continua en un punto y no ser derivable en ese punto. Esto ocurre en los puntos angulosos o angulares y en los puntos cuya tangente es una recta vertical (perpendicular al eje X).
DERIVABLE IMPLICA CONTINUIDAD
Si una función es derivable en un punto, necesariamente es continua en él. No ocurre en sentido contrario como se ha demostrado en los ejemplos anteriores.


 INICIO
INICIO

