Interpretación geométrica de la derivada
Pendiente de una recta
Recordamos primero que la pendiente de una recta dada es el cociente:
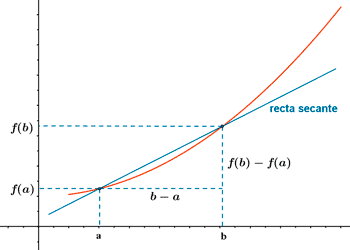
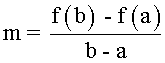
Si hacemos b = a + h obtenemos la siguiente expresión:
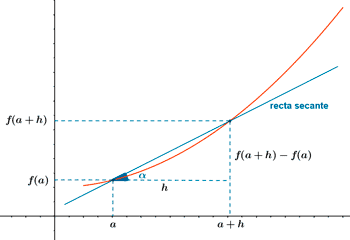
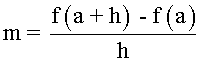
![]()
Pendiente de una curva en un punto P(a, f(a))
La pendiente de una curva en un punto P(a, f(a)) se define como la pendiente de la recta que más se acerca a la curva en dicho punto.
A esta recta se le llama tangente a la curva en P.
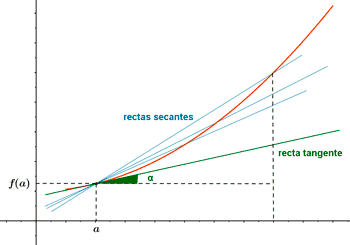
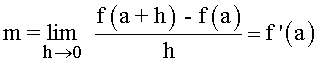
Geométricamente la derivada f '(a) es la pendiente de la recta tangente a la gráfica de la función en el punto P(a, f(a)).
La pendiente de la gráfica de una función lineal
Encontrar la pendiente de la gráfica f(x) = 3x - 5 en el punto (2, 1) .
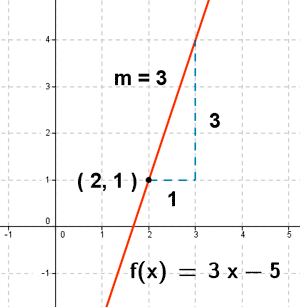
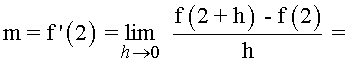
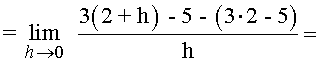
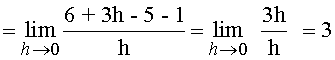
La pendiente de la función en el punto P(2,1) es m = 3 .
Rectas tangentes a la gráfica de una función no lineal
Calcula las pendientes de las rectas tangentes a la gráfica de la función f(x) = x2 - 1 en los puntos (2, 3) y (0, -1) .
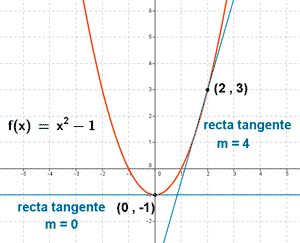
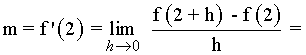
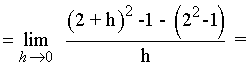
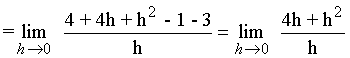
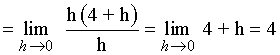
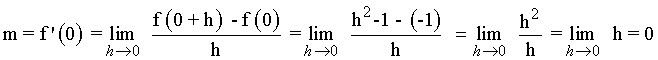
Tangentes verticales
Si una función f(x) es continua en el punto P(a, f(a)) si:
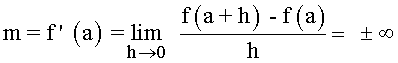
entonces la recta vertical x = a es tangente vertical a la gráfica de y = f(x) en el punto P .
Si aparte de que el resultado sea ±∞ el límite del cociente no existe, la gráfica y = f(x) no tiene tangente en el punto P .
Ejemplo de recta tangente vertical
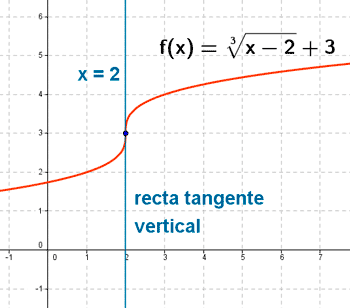
La función f(x) tiene una recta tangente vertical en el punto (2, 3) que corresponde con x = 2 .
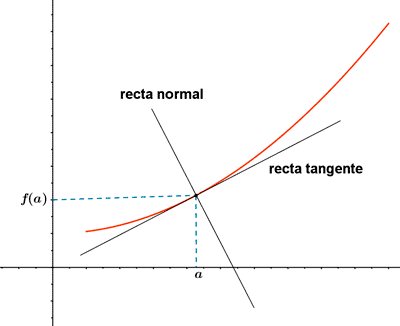
Ecuaciones de la recta tangente y de la recta normal
La ecuación de la recta tangente a la gráfica de la función en el punto P(a, f(a)) es:
![]()
La ecuación de la recta normal a la gráfica de la función en el punto P(a, f(a)) es la recta perpendicular a la recta tangente, siendo su ecuación:

Cálculo de la recta tangente y normal a una curva
1) Calcula las ecuaciones de las rectas tangente y normal a la curva f(x) = x2 - 4 en el punto (1, -3) .
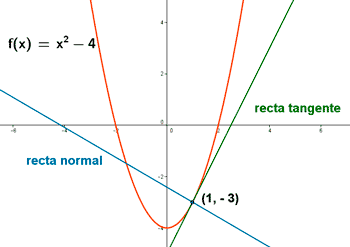
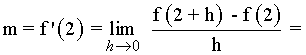
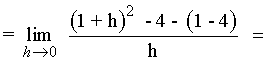
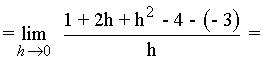
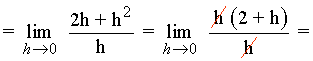
![]()
La ecuación de la recta tangente es:
![]()
![]()
![]()
![]()
Y la ecuación de la recta normal:
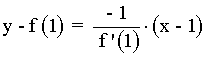
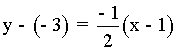
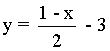
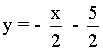
2) Calcula las ecuaciones de las rectas tangente y normal a la curva f(x) = -6/x en el punto (-2, 3) .
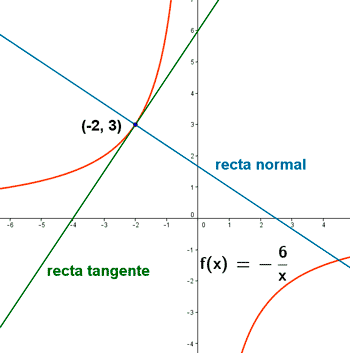
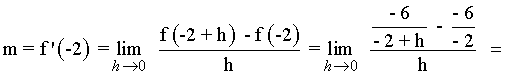
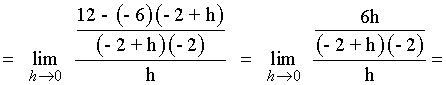
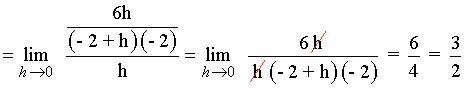
La ecuación de la recta tangente es:
![]()
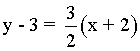
![]()
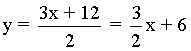
Y la ecuación de la recta normal:
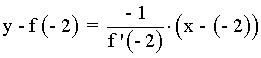
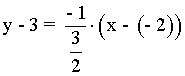
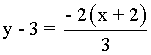
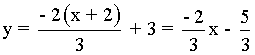


 INICIO
INICIO
