Composición de funciones
Sean f y g dos funciones reales de variable real y de dominios Dom(f) y Dom(g) respectivamente, y tales que f(Dom(f)) ⊆ Dom(g).
Llamamos función compuesta de f con g a la función:
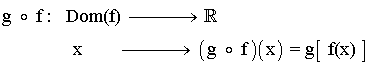
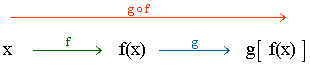
La expresión (g o f)(x) se lee como f compuesta con g de x. Para nombrarla, se comienza por la función de la derecha, porque es la primera que actúa sobre la variable x.
En general, (g o f)(x) es distinto que (f o g)(x). Es decir, la composición de funciones no cumple la propiedad conmutativa.
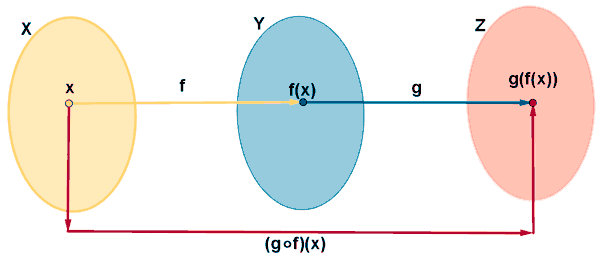
La condición f(Dom(f)) ⊆ Dom(g) es necesaria para calcular la función (g o f), ya que si hubiese un valor x0 ∈ Dom(f) tal que f(x0) ∉ Dom(g), entonces g[ f(x) ] no existiría y (g o f) no estaría definida para x0.
Por tanto, el dominio máximo de la función compuesta (g o f) será Dom(f), pero puede ser un subconjunto suyo, es decir:
Dom(g o f) ⊆ Dom(f)


 INICIO
INICIO

