Ejercicios de composición de funciones
Dadas las funciones:
![]()
Calcula las composiciones de funciones siguientes, y calcula el valor de cada composición para x = 0.
1) f o g
2) g o f
3) f o h
4) h o f
5) g o h
6) h o g
Comprueba que la composición de funciones no es conmutativa.
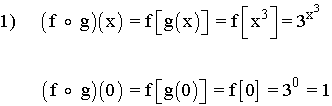
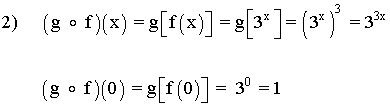
(f o g)(x) ≠ (g o f)(x) , la composición no es conmutativa.
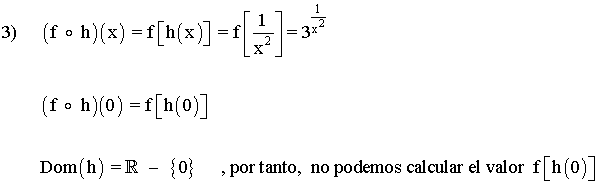
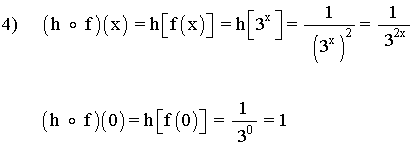
(f o h)(x) ≠ (h o f)(x) , la composición no es conmutativa.
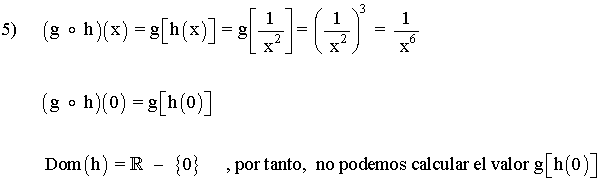
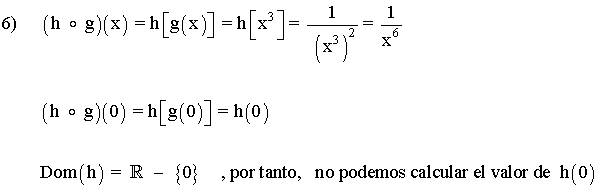
(g o h)(x) = (h o g)(x) , en este caso, la composición sí es conmutativa. Pero hemos visto que, en general, no tiene por qué serlo.
Dadas las funciones:
![]()
Calcula las composiciones de funciones siguientes:
1) f o g
2) g o f
3) f o h
4) h o f
5) g o h
6) h o g
![]()
![]()
![]()
![]()
![]()
![]()
Dadas las funciones:
![]()
Calcula: (f o g)(x) y (g o f)(x)
Comprueba que la composición de funciones no es conmutativa.
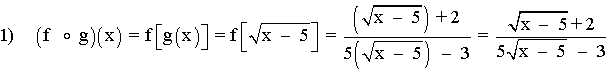
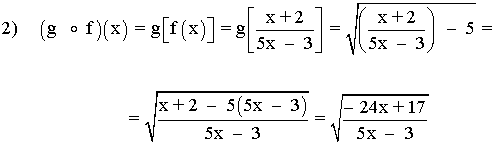
(f o g)(x) ≠ (g o f)(x) , la composición no es conmutativa.
Dadas las funciones:
![]()
Calcular:
1) (f o g)(x) y su dominio.
2) (g o f)(x) y su dominio.
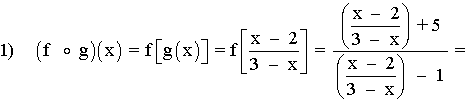
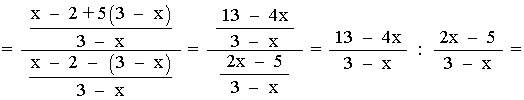
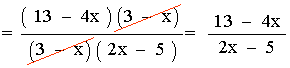
Dom(g) = R - {3}
Observamos que: 2x - 5 = 0 ⇔ x = 5/2
Dom(f o g) = { x∈Dom(g) | g(x)∈Dom(f) } = R - {3, 5/2}
La intersección de los dos dominios es el dominio de la composición.
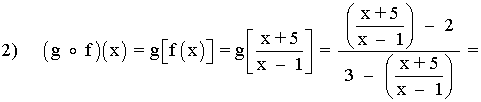
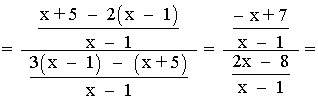
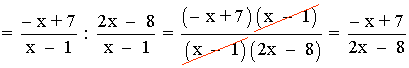
Dom(f) = R - {1}
Observamos que: 2x - 8 = 0 ⇔ x = 4
Dom(g o f) = { x∈Dom(f) | f(x)∈Dom(g) } = R - {1, 4}
La intersección de los dos dominios es el dominio de la composición.
Dadas las funciones:
![]()
Calcular:
1) (f o g)(x) y su dominio.
2) (g o f)(x) y su dominio.
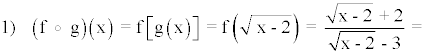
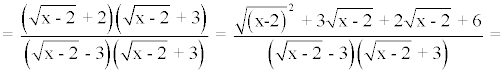
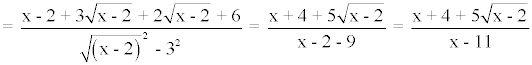
La raíz está definida siempre que el radicando sea positivo o cero:
Dom(g) = [2, +∞)
La fracción está definida para x - 11 ≠ 0
Observamos que: x - 11 = 0 ⇔ x = 11
Además se debe cumplir que: x ≥ 2
Dom(f o g) = { x∈Dom(g) | g(x)∈Dom(f) } = [2, 11) ∪ (11, + ∞)
La intersección de los dos dominios es el dominio de la composición.
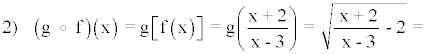
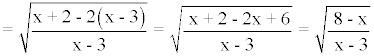
La fracción está definida para x - 3 ≠ 0
Dom(f) = R - {3}
En la composición observamos que se debe cumplir que:
![]()
Sustituimos un valor en cada intervalo:
(- ∞, 3) para x = 0 - 8/3 < 0
(3, 8] para x = 4 4 > 0
[8, + ∞) para x = 9 - 1/3 < 0
Es decir, está definida en el intervalo (3, 8]
Dom(g o f) = { x∈Dom(f) | f(x)∈Dom(g) } = (3, 8]
La intersección de los dos dominios es el dominio de la composición.
Dadas las funciones:
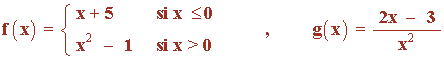
Calcula (f o g)(x)
Para x ≤ 0 :
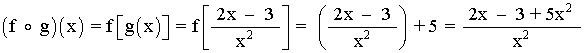
Para x > 0 :
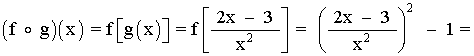
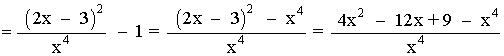
Por tanto:
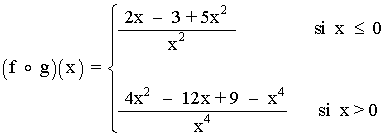
Dadas las funciones f(x) = 3x - 7 , g(x) = 2x + k determinar k para que: (f o g)(x) = (g o f)(x)
(f o g)(x) = f[ g(x) ] = f[ 2x + k ] = 3(2x + k) - 7 = 6x + 3k - 7
(g o f)(x) = g[ f(x) ] = g[ 3x - 7 ] = 2(3x - 7) + k = 6x - 14 + k
Queremos que (f o g)(x) = (g o f)(x), así que igualamos ambos resultados:
6x + 3k - 7 = 6x - 14 + k
Despejamos la variable k:
6x + 3k - 7 = 6x - 14 + k ⇔ 6x + 3k - 7 = 6x - 14 + k ⇔ 3k - k = - 14 + 7 ⇔ 2k = - 7 ⇔ k = - 7/2
Por tanto, las composiciones (f o g) y (g o f) serán conmutativas si k = - 7/2.
Expresar esta función como composición de otras funciones más sencillas:
![]()
Primero se divide la función en funciones más sencillas:
f1(x) = x3 - 2
f2(x) = ln x
f3(x) = sen x
En segundo lugar se componen las funciones para comprobar que el restultado:
![]()


 INICIO
INICIO