Ejercicios de función inversa
- 1. Lineales
- 2. Cuadráticas
- 3. Racionales
- 4. Irrac.
- 5. Exp.
- 6. Trigo.
- 7. V. abs.
- 8. Propiedades I
- 9. II
- 10. III
Calcula la función inversa y comprueba que sus gráficas son simétricas respecto a la bisectriz del primer y tercer cuadrante:
1) f(x) = 7
Esta función no es inyectiva, puesto que:
f(1) = f(2)
Es decir, dos elementos distintos tienen la misma imagen.
Por lo tanto, f -1 no existe.
2) f(x) = 2x - 5
Veamos primero si la función es inyectiva, es decir, si dos elementos son distintos tienen imágenes distintas.
f(x1) = f(x2) ⇒ 2x1 - 5 = 2x2 - 5 ⇒ 2x1 = 2x2 ⇒ x1 = x2
Se realiza la comprobación al revés. Si dos imágenes son iguales, sus originales deben ser iguales.
En segundo lugar, despejamos la variable x de la ecuación: y = f(x)
y = 2x - 5
y + 5 = 2x
x = (y + 5)/2
Por último intercambiamos las variables:
![]()
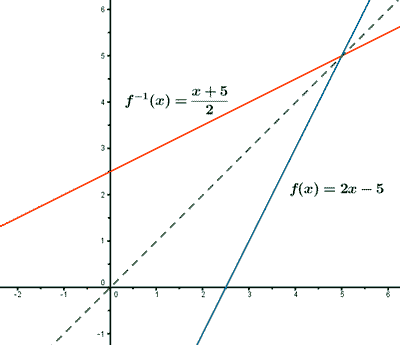
Calcula la función inversa y comprueba que sus gráficas son simétricas respecto a la bisectriz del primer y tercer cuadrante:
1) f(x) = x2 + 2
Veamos primero si la función es inyectiva, es decir, si dos elementos son distintos tienen imágenes distintas.
Esta función no es inyectiva: f(- 1) = f(1) = 3 , dos elementos distintos tienen la misma imagen.
Para valores reales positivos de la función ( x ≥ 0) podemos obtener su inversa, despejando la variable x :
![]()
Por último, intercambiamos las variables:
![]()
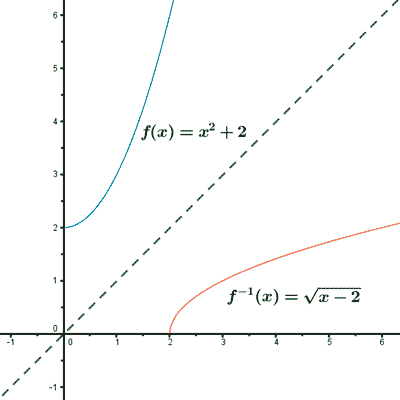
2) f(x) = (x + 1)2
Veamos primero si la función es inyectiva, es decir, si dos elementos son distintos tienen imágenes distintas.
f(x1) = f(x2) ⇒ (x1 + 1)2 = (x2 + 1)2 ⇒ x1 + 1 = x2 + 1 ⇒ x1 = x2
Por lo tanto la función es inyectiva.
En segundo lugar, despejamos la variable x de la ecuación: y = f(x)
Por último, intercambiamos las variables:
![]()
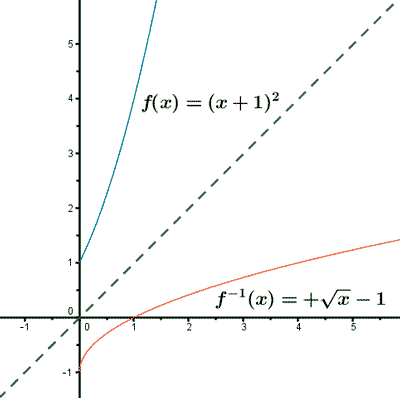
Calcula la función inversa y comprueba que sus gráficas son simétricas respecto a la bisectriz del primer y tercer cuadrante:
![]()
Veamos primero si la función es inyectiva, es decir, si dos elementos son distintos tienen imágenes distintas.
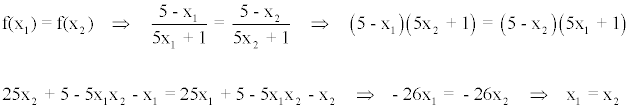
Por lo tanto la función es inyectiva.
En segundo lugar, despejamos la variable x de la ecuación: y = f(x)
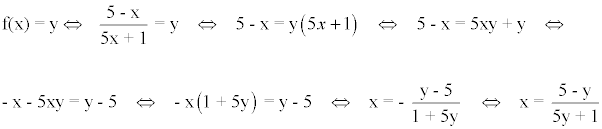
Por último, intercambiamos las variables:
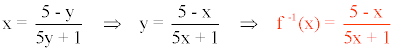
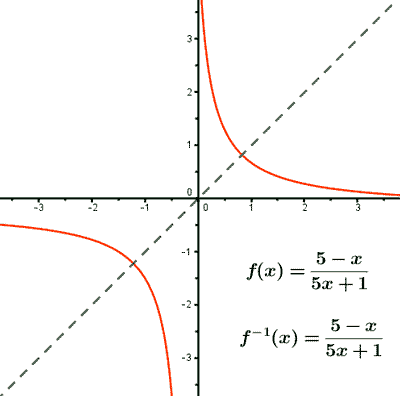
Calcula la función inversa y comprueba que sus gráficas son simétricas respecto a la bisectriz del primer y tercer cuadrante:
![]()
Veamos primero si la función es inyectiva, es decir, si dos elementos son distintos tienen imágenes distintas.
![]()
Por lo tanto la función es inyectiva.
En segundo lugar, despejamos la variable x de la ecuación: y = f(x)
![]()
Por último, intercambiamos las variables:
![]()
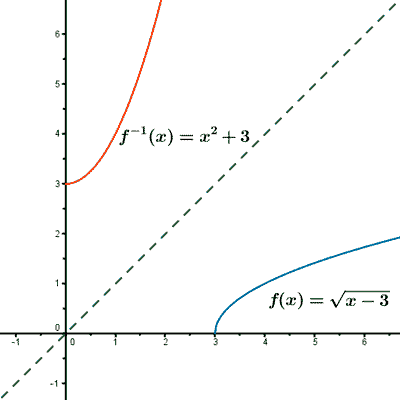
![]()
Veamos primero si la función es inyectiva, es decir, si dos elementos son distintos tienen imágenes distintas.
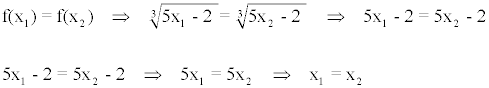
Por lo tanto la función es inyectiva.
En segundo lugar, despejamos la variable x de la ecuación: y = f(x)
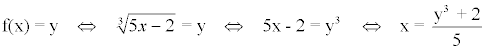
Por último, intercambiamos las variables:
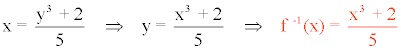
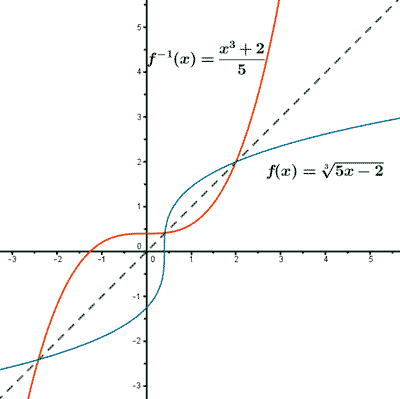
Calcula la función inversa y comprueba que sus gráficas son simétricas respecto a la bisectriz del primer y tercer cuadrante:
![]()
Veamos primero si la función es inyectiva, es decir, si dos elementos son distintos tienen imágenes distintas.
![]()
Por lo tanto la función es inyectiva.
Despejamos la variable x de la ecuación: y = f(x)
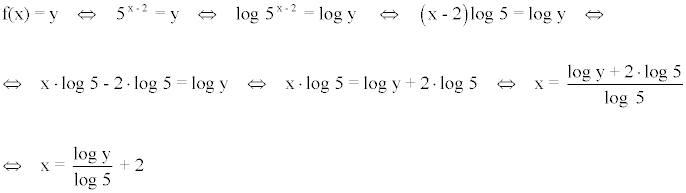
A continuación, intercambiamos las variables:
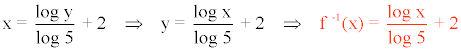
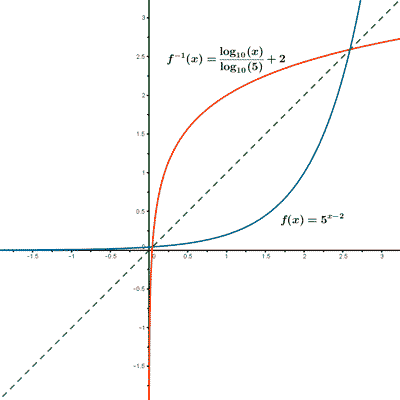
![]()
Veamos primero si la función es inyectiva, es decir, si dos elementos son distintos tienen imágenes distintas.
![]()
Por lo tanto la función es inyectiva.
Despejamos la variable x de la ecuación: y = f(x)
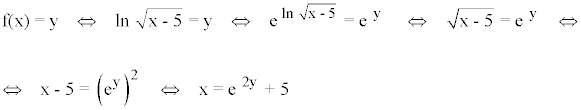
A continuación, intercambiamos las variables:
![]()
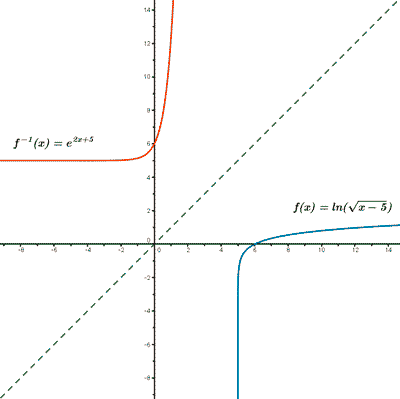
Calcula la función inversa de las siguientes funciones:
![]()
Despejamos la variable x de la ecuación: y = f(x)
![]()
A continuación, intercambiamos las variables:
![]()
![]()
Despejamos la variable x de la ecuación: y = f(x)
![]()
A continuación, intercambiamos las variables:
![]()
![]()
Despejamos la variable x de la ecuación: y = f(x)
A continuación, intercambiamos las variables:
![]()
Calcula la función inversa de las siguientes funciones:
1) y = |x - 2|
En primer lugar definimos la función en intervalos:
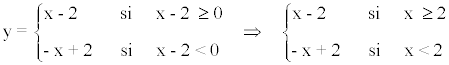
Despejamos la variable x de la ecuación: y = f(x) en cada rama:
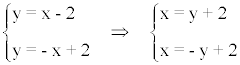
A continuación, intercambiamos las variables:
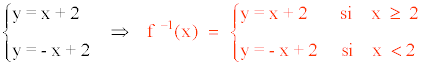
2) y = |4 - x2|
En primer lugar definimos la función en intervalos:
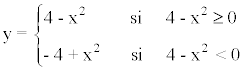
Resolvemos la inecuación: 4 - x2 ≥ 0
Las raíces de 4 - x2 = 0 son x = ± 2
A continuación estudiamos el signo en los siguientes intervalos:
• A = (-∞, -2) ⇒ Para x = - 3 tenemos que f(-3) = 4 - (-3)2 = 4 - 9 = - 5 < 0
• B = (-2, 2) ⇒ Para x = 0 tenemos que f(0) = 4 - (0)2 = 4 - 0 = 4 > 0
• C = (2, +∞) ⇒ Para x = 3 tenemos que f(3) = 4 - (3)2 = 4 - 9 = - 5 < 0
Por lo tanto la función original queda definida de la siguiente manera:
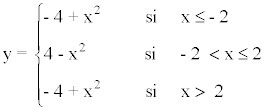
Despejamos la variable x de la ecuación: y = f(x) en cada rama:
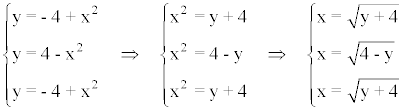
A continuación, intercambiamos las variables:
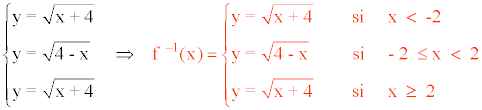
Calcula la función inversa de las siguientes funciones y comprueba que la función dada, compuesta con su inversa, da la función identidad:
1) f(x) = 1 - 3x
Veamos primero si la función es inyectiva, es decir, si dos elementos son distintos tienen imágenes distintas.
![]()
Por lo tanto la función es inyectiva.
Despejamos la variable x de la ecuación: y = f(x)
![]()
A continuación, intercambiamos las variables:
![]()
Comprobamos que la composición de la función original con su inversa resulta la función identidad:
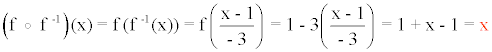
2) f(x) = x3 - 5
Despejamos la variable x de la ecuación: y = f(x)
![]()
A continuación, intercambiamos las variables:
![]()
Comprobamos que la composición de la función original con su inversa resulta la función identidad:
![]()
3) f(x) = 3x + 3
Despejamos la variable x de la ecuación: y = f(x)
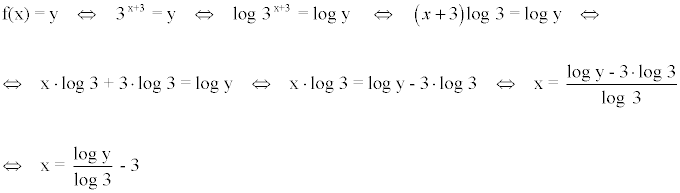
A continuación, intercambiamos las variables:
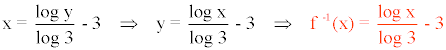
Comprobamos que la composición de la función original con su inversa resulta la función identidad:
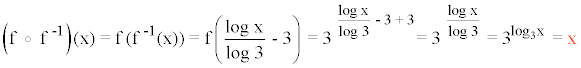
Hemos aplicado la propiedad del cambio de base:
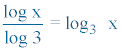
Calcula (f o g)-1 y (f o g)-1(2)
![]()
En primer lugar calculamos f o g(x) :
![]()
Para calcular la función inversa, comprobamos si f o g(x) es inyectiva:
![]()
Despejamos la variable x de la ecuación: y = f o g(x)
![]()
A continuación, intercambiamos las variables:
![]()
De esta forma tenemos que:
![]()
Comprueba que (f o g)-1 = g-1 o f-1
![]()
Calculamos en primer lugar f o g(x) :
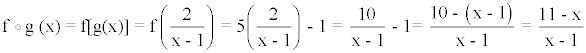
A continuación calculamos su inversa despejando la variable x :
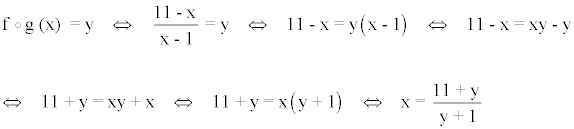
Realizamos el intercambio de variables:
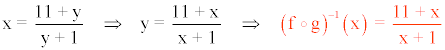
Ahora calculamos la función inversa de f(x) despejando la variable x :
![]()
Realizando el intercambio de variables tenemos que:
![]()
Calculamos también la función inversa de g(x) :
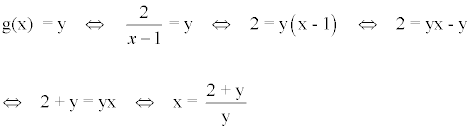
Realizando el intercambio de variables tenemos que:
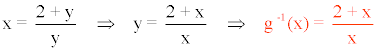
Por último, calculamos g-1 o f -1 :
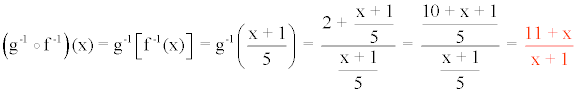


 INICIO
INICIO