Matriz inversa
Para los números reales sabemos que existe un elemento neutro para el producto, el 1, de manera que si a es un real no nulo, existe un único número real b de manera que a · b = b · a = 1.
Por otra parte, sabemos que para el producto de matrices cuadradas de orden n, el elemento neutro es la matriz In. Es natural plantearse la siguiente pregunta:
¿Dada una matriz A de orden n existirá siempre una matriz B tal que A · B = B · A = In?
Respuesta: No siempre existe la matriz inversa, pero en caso de existir es única.
Dada una matriz cuadrada A de orden n, llamaremos matriz inversa de A y representaremos por A-1 a la matriz de orden n que verifica:
A · A-1 = A-1 · A = In
donde In representa a la matriz identidad de orden n.
Si A tiene inversa se dice que A es inversible o regular.
Si no existe A-1 se dice que A es no inversible o singular.
Ejemplo:
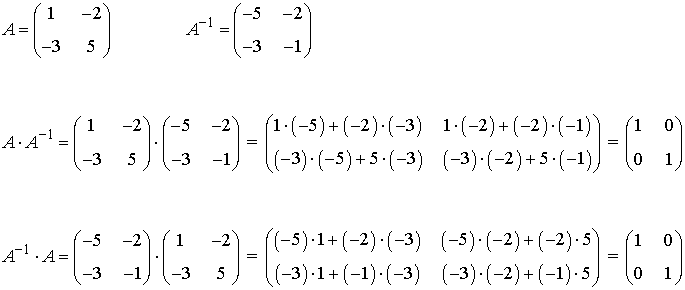
Propiedades de la inversión de matrices
Si A y B son dos matrices de orden n inversibles se verifican las siguientes propiedades- A-1 es inversible y (A-1)-1 = A
- A · B es inversible y su inversa es (A · B)-1 = B-1 · A-1
- At es inversible y (At)-1 = (A-1)t
Cálculo de la matriz inversa por definición
Ejemplo de cálculo de la matriz inversa por definición:
Calcular la matriz inversa de A y comprobar que lo es multiplicándola por la dada.
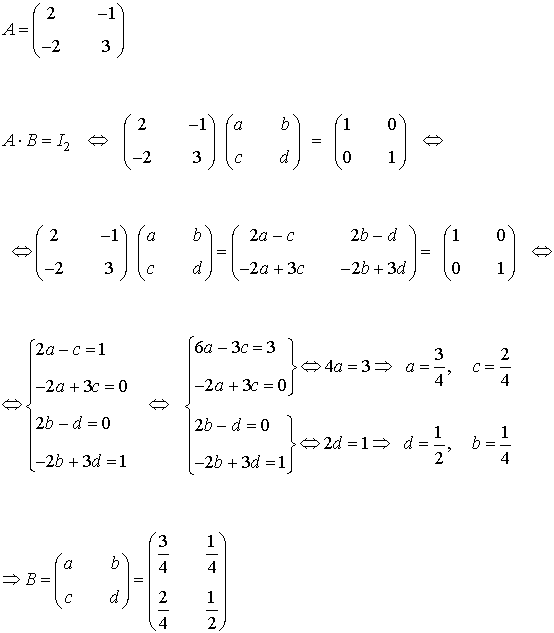
Nuestra candidata a matriz inversa es la matriz B. Comprobamos que efectivamente es la inversa de A:
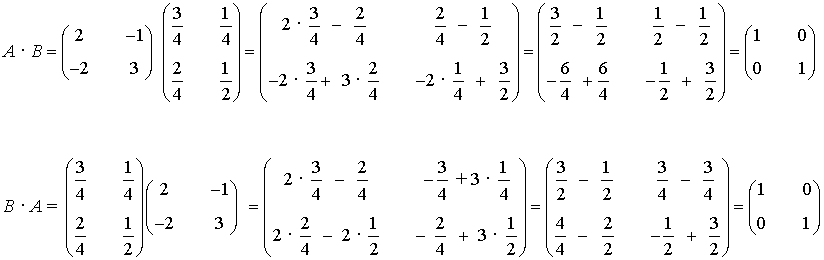
Por tanto B es la inversa de A, de manera que A-1 = B.
Cálculo de la matriz inversa por el método de Gauss-Jordan
El método de Gauss-Jordan permite hallar la inversa de una matriz realizando transformaciones elementales:
- Cambiar el orden de las filas.
- Multiplicar una o más filas por un número real distinto de cero.
- Sumar a una fila otra multiplicada por un número real.
Para aplicar el método procedemos como sigue:
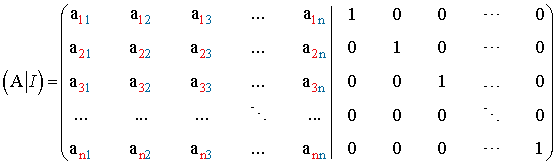
- Partimos de una matriz formada por A y una matriz identidad del mismo orden que A. Esta matriz recibe el nombre de matriz ampliada y se simboliza por ( A | I ) :
- Aplicamos transformaciones elementales hasta llegar a una matriz ampliada ( I | B) :
- La matriz B (en caso de poder llegar a la matriz ampliada (I | B) mediante transformaciones elementales) resulta ser A-1
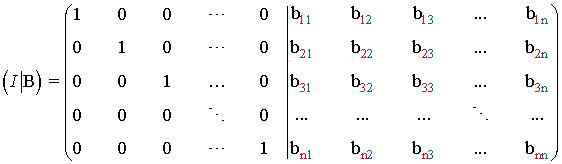
Ejemplo de cálculo de la matriz inversa por el método de Gauss-Jordan:
Calcular la matriz inversa de:
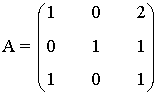
por el método de Gauss-Jordan
- Cambiar el orden de las filas.
- Multiplicar una o más filas por un número real distinto de cero.
- Sumar a una fila otra multiplicada por un número real.
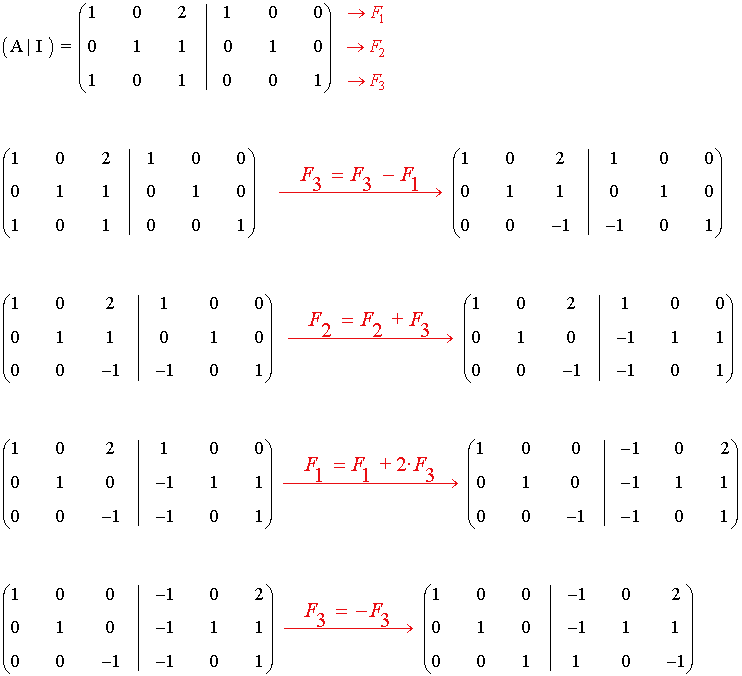
de manera que existe A-1 siendo:
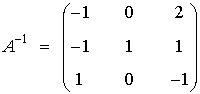


 INICIO
INICIO

