Ejercicios resueltos de potencias de matrices
1) Sea la matriz:
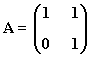
a) Calcular A2 y A3
b) Halla una ley general para calcular An
c) Calcular A10
2) Sea la matriz:
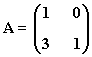
a) Calcular An
b) Calcular A350-A250
3) Sea la matriz:
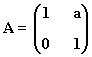
a) Calcula An
b) Halla A22-12A2+2A
4) Sea la matriz:
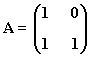
a) Calcula An
b) Halla A250+A20
5) Calcula An para todo valor de n entero positivo y A la siguiente matriz:
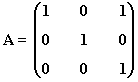
6) Calcula An para todo valor de n entero positivo y A la siguiente matriz:
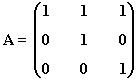
7) Sea la matriz:
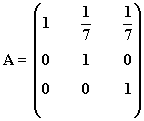
a) Calcula An
b) Halla A35
8) Calcula An para todo valor de n entero positivo y A la siguiente matriz:
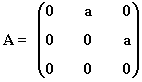
9) Se considerann las siguientes:
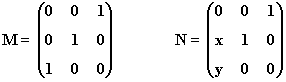
a) Determina x e y para que MN = NM
b) Halla M1995 y M1996
10) Halla todas las matrices X de la siguiente forma
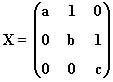
tales que:
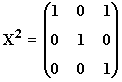
11) Se consideran las matrices:

Calcular B3 y A3 (Sugerencia: A = B + I)
12) Sea la matriz:
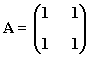
Prueba que An=2n-1·A
13) Sea la matriz:
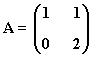
Calcula An
14) Sea la matriz:
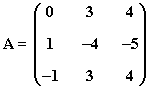
Prueba que se verifica que A3 + I = 0 y utiliza esta igualdad para obtener A10
15) Sea la matriz:
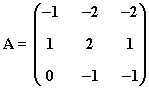
a) Comprueba que verifica que A3 + I = 0
b) Calcula A13
c) Basándote en los apartados anteriores y sin recurrir al cálculo de inversas, halla la matriz X que verifica la igualdad A2X + I = A
1) Sea la matriz:
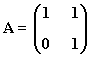
a) Calcular A2 y A3
b) Halla una ley general para calcular An
c) Calcular A10
Aplicamos el método de inducción:
Primer paso: Se calculan las primeras potencias de A:
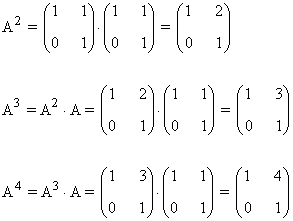
Segundo paso: A partir del resultado anterior, suponemos que:
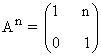
Tercer paso: Se comprueba el resultado para la siguiente potencia An+1
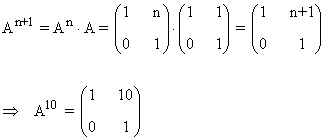
2) Sea la matriz:
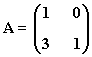
a) Calcular An
b) Calcular A350-A250
Aplicamos el método de inducción:
Primer paso: Se calculan las primeras potencias de A:
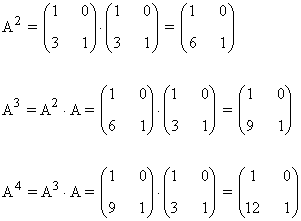
Segundo paso: A partir del resultado anterior, suponemos que:
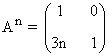
Tercer paso: Se comprueba el resultado para la siguiente potencia An+1
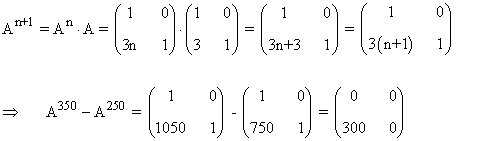
3) Sea la matriz:
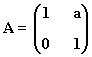
a) Calcula An
b) Halla A22-12A2+2A
Aplicamos el método de inducción:
Primer paso: Se calculan las primeras potencias de A:
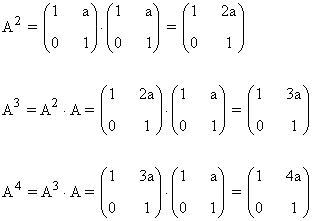
Segundo paso: A partir del resultado anterior, suponemos que:
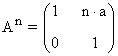
Tercer paso: Se comprueba el resultado para la siguiente potencia An+1
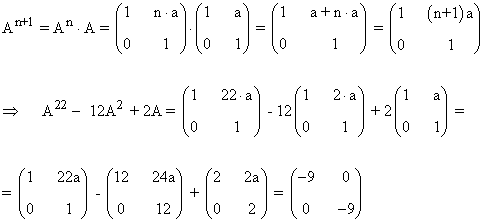
4) Sea la matriz:
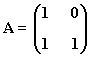
a) Calcula An
b) Halla A250+A20
Aplicamos el método de inducción:
Primer paso: Se calculan las primeras potencias de A:
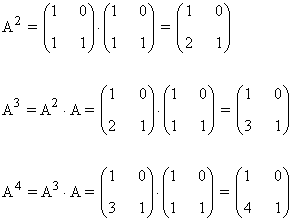
Segundo paso: A partir del resultado anterior, suponemos que:
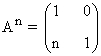
Tercer paso: Se comprueba el resultado para la siguiente potencia An+1
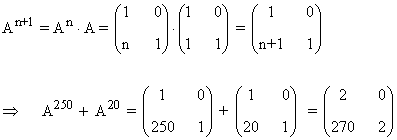
5) Calcula An para todo valor de n entero positivo y A la siguiente matriz:
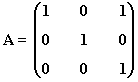
Aplicamos el método de inducción:
Primer paso: Se calculan las primeras potencias de A:
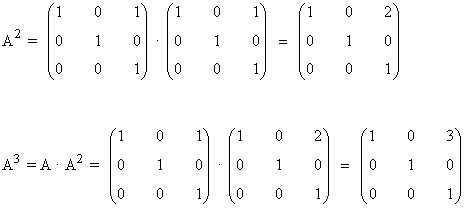
Segundo paso: A partir del resultado anterior, suponemos que:
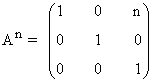
Tercer paso: Se comprueba el resultado para la siguiente potencia An+1
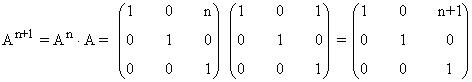
Por lo tanto, hemos demostrado que:
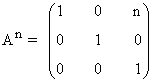
6) Calcula An para todo valor de n entero positivo y A la siguiente matriz:
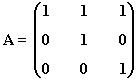
Aplicamos el método de inducción:
Primer paso: Se calculan las primeras potencias de A:
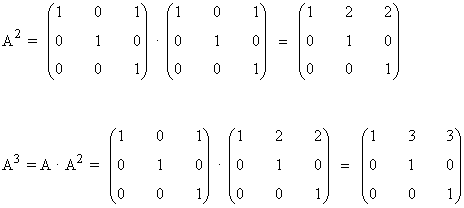
Segundo paso: A partir del resultado anterior, suponemos que:
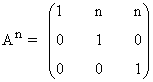
Tercer paso: Se comprueba el resultado para la siguiente potencia An+1
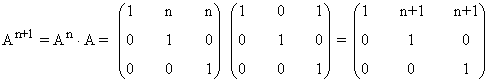
Por lo tanto, hemos demostrado que:
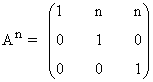
7) Sea la matriz:
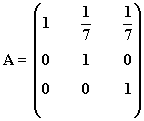
a) Calcula An
b) Halla A35
Aplicamos el método de inducción:
Primer paso: Se calculan las primeras potencias de A:
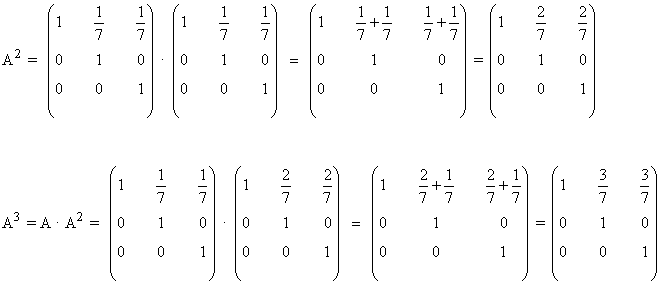
Segundo paso: A partir del resultado anterior, suponemos que:
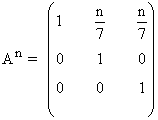
Tercer paso: Se comprueba el resultado para la siguiente potencia An+1
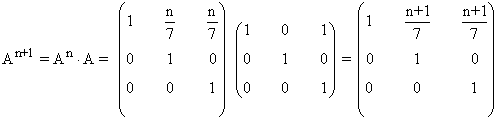
Por lo tanto, hemos demostrado que:
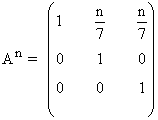
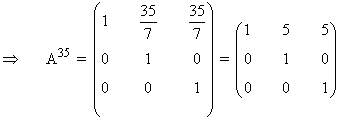
8) Calcula An para todo valor de n entero positivo y A la siguiente matriz:
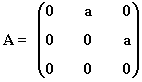
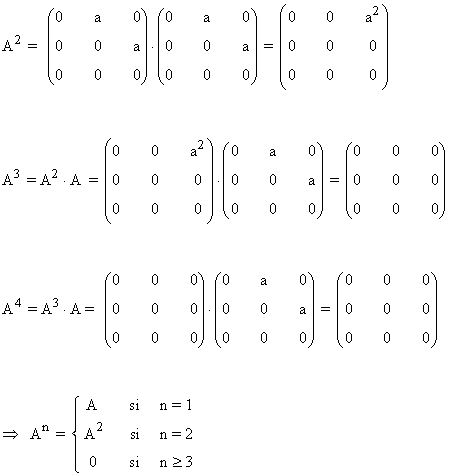
9) Se considerann las siguientes:
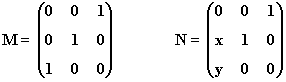
a) Determina x e y para que MN = NM
b) Halla M1995 y M1996
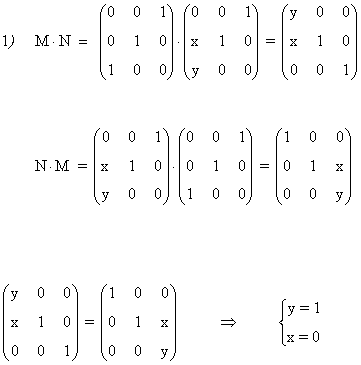
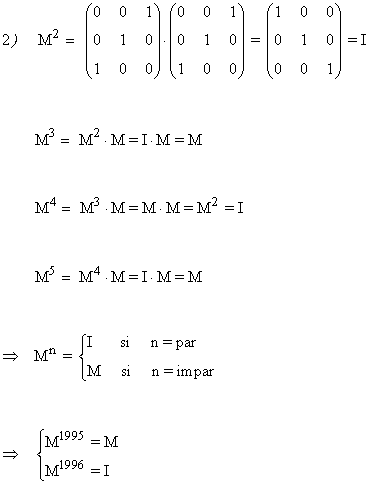
10) Halla todas las matrices X de la siguiente forma
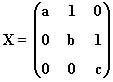
tales que:
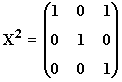
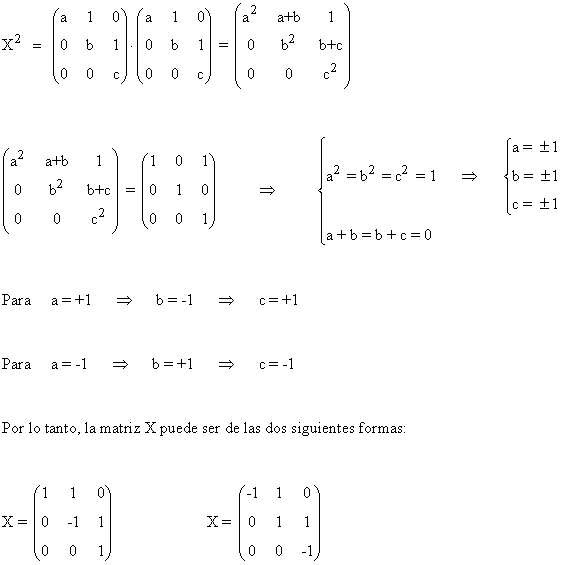
11) Se consideran las matrices:

Calcular B3 y A3 (Sugerencia: A=B+I)

12) Sea la matriz:
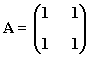
Prueba que An=2n-1·A
Aplicamos el método de inducción:
Primer paso: Se calculan las primeras potencias de A:
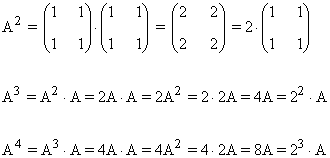
Segundo paso: A partir del resultado anterior, suponemos que:
![]()
Tercer paso: Se comprueba el resultado para la siguiente potencia An+1
![]()
Por lo tanto, hemos demostrado que:
![]()
13) Sea la matriz:
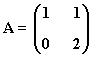
Calcula An
Aplicamos el método de inducción:
Primer paso: Se calculan las primeras potencias de A:
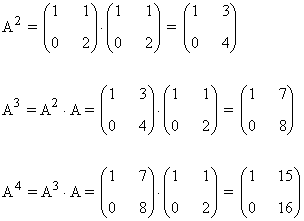
Segundo paso: A partir del resultado anterior, suponemos que:
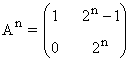
Tercer paso: Se comprueba el resultado para la siguiente potencia An+1
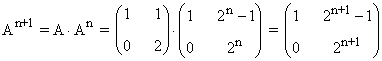
Por lo tanto, hemos demostrado que:
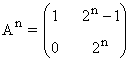
14) Sea la matriz:
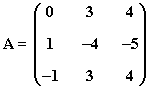
Prueba que se verifica que A3 + I = 0 y utiliza esta igualdad para obtener A10
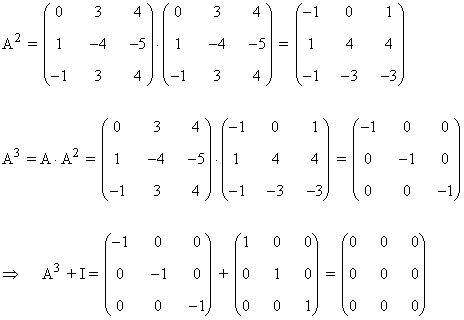
Sabiendo que A3 + I = 0 , tenemos que: A3 = - I
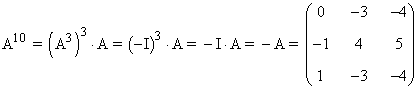
15) Sea la matriz:
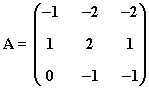
a) Comprueba que verifica que A3 + I = 0
b) Calcula A13
c) Basándote en los apartados anteriores y sin recurrir al cálculo de inversas, halla la matriz X que verifica la igualdad A2X + I = A
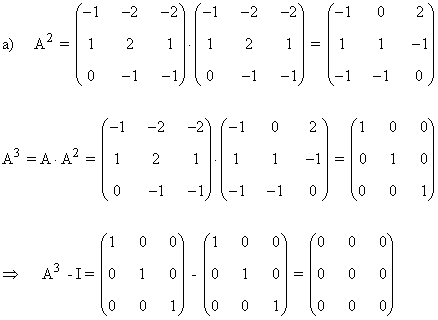
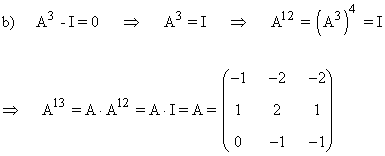
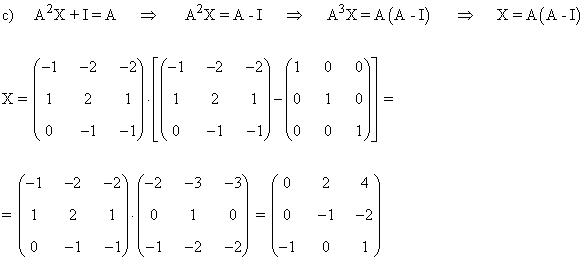


 INICIO
INICIO