Ejercicios resueltos de Selectividad de matrices
•Ejercicios de operaciones con matrices:
1) Sean las matrices:
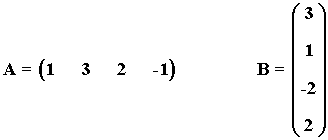
Efectuar las siguientes operaciones: a) A·B b) B·A
2) Sean las matrices:

a) Calcule AB y BA
b) Compruebe que (A+B)2 = A2+B2
3) Sea la matriz:
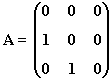
a) Encuentra las matrices B cuyo producto con A verifique la propiedad conmutativa (AB = BA)
b) Calcula An
•Ejercicios de inversa de matrices:
4) Dada la matriz A:
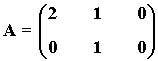
1) Razona si puede existir una matriz B tal que AB = I,
siendo I la matriz identidad. En caso afirmativo halla B.
2) ¿Tiene inversa A? Razona la respuesta.
5) Calcula por el método de Gauss-Jordan la matriz inversa de las siguientes matrices:
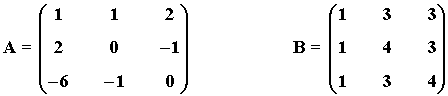
6) Considera la matriz:
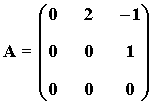
Prueba que B = I + A + A2 es la matriz inversa de I - A ,
donde I es la matriz identidad de orden 3
7) Considera la matriz:
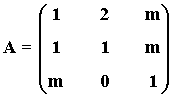
donde m∈IR . Determina para qué valores de m la matriz A es regular (inversible)
8) Consideremos la matriz A:
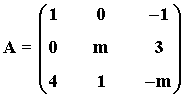
a) Averigua para que valores del parámetro m la matriz no tiene inversa
b) Calcula, si es posible, la matriz inversa de A para m = 2
9) Se consideran las matrices:
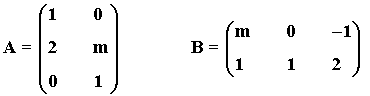
a) Estudia, en función de los valores reales de m ,
si la matriz B·A tiene inversa
b) Haz lo mismo para la matriz A·B
•Ejercicios de potencia de matrices:
10) Sea la matriz:
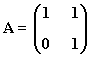
a) Calcular A2 y A3
b) Halla una ley general para calcular An
c) Calcular A10
11) Sea la matriz:
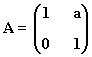
a) Calcula An
b) Halla A22-12A2+2A
12) Sea la matriz:
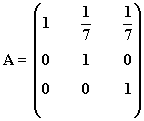
a) Calcula An
b) Halla A35
13) Se considerann las siguientes:
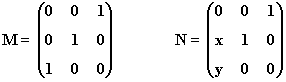
a) Determina x e y para que MN = NM
b) Halla M1995 y M1996
14) Sea la matriz:
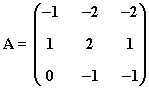
a) Comprueba que verifica que A3 + I = 0
b) Calcula A13
c) Basándote en los apartados anteriores y sin recurrir al cálculo de inversas, halla la matriz X que verifica la igualdad A2X + I = A
•Ejercicios de rango de matrices:
15) Hallar el rango de la matriz B utilizando el método de Gauss:
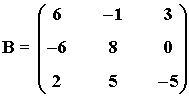
16) Hallar el rango de la matriz B utilizando el método de Gauss:
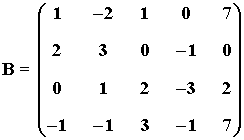
17) Haz uso del método de Jordan y discute el rango de la matriz A
según los valores del parámetro m :
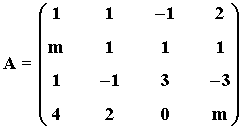
18) Dada la siguiente matriz:
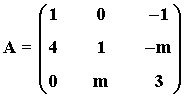
a) Determinar los valores de m para que rango(A) < 3
b) ¿Puede ser rango (A) = 1 para algún valor de m ?
•Ejercicios de ecuaciones matriciales:
19) Dadas las matrices
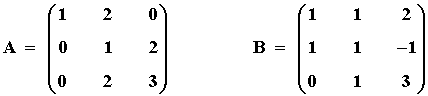
a) Determinar la matriz inversa de B
b) Determinar una matriz X tal que A = B·X
20) Considera las matrices:
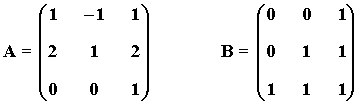
Calcula la matriz X que verifica AX + B = I ,
donde I representa la matriz identidad.
21) Determinar la matriz X en la siguiente ecuación matricial:
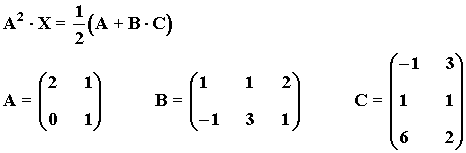
22) Consideremos las siguientes matrices:
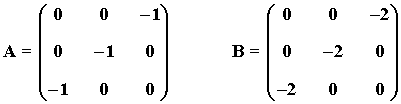
Calcular una matriz cuadrada X sabiendo que verifica X·A2 + B·A = A2
•Ejercicios de sistemas matriciales:
23) Dadas las matrices:
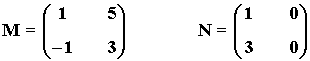
halla dos matrices X e Y que verifiquen:
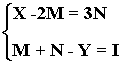
24) Halla las matrices X e Y que verifican el sistema:
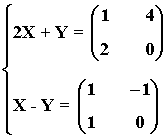
25) Halla dos matrices A y B tales que:
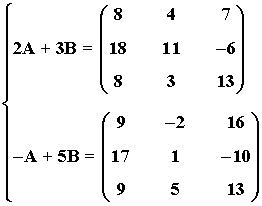
1) Sean las matrices:
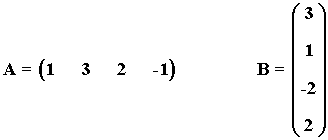
Efectuar las siguientes operaciones:
a) A·B b) B·A
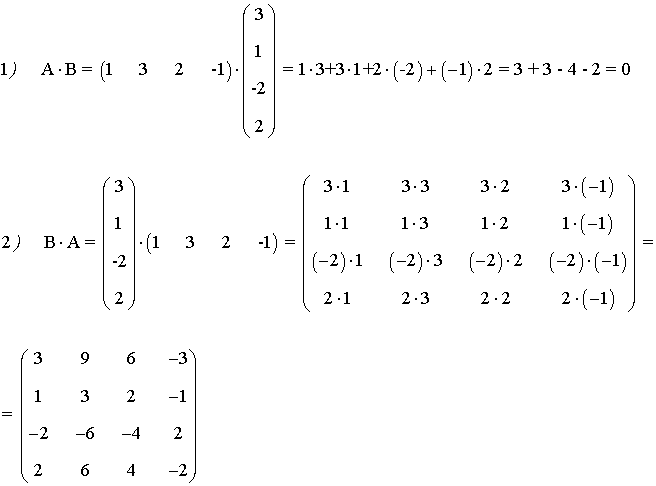
2) Sean las matrices:

a) Calcule AB y BA
b) Compruebe que (A+B)2 = A2+B2
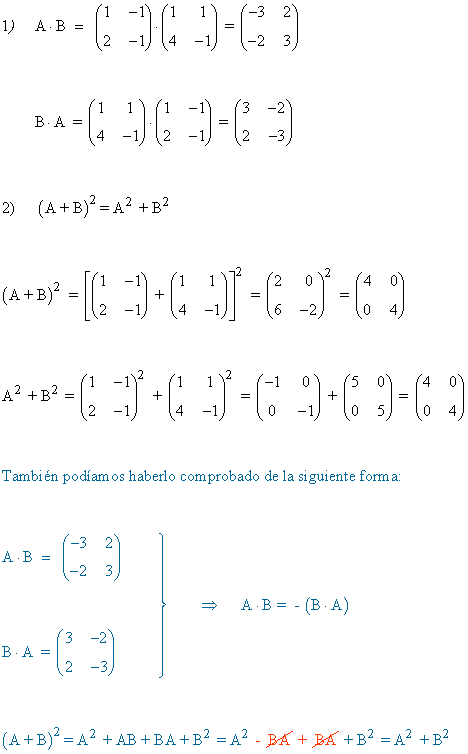
3) Sea la matriz:
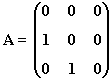
a) Encuentra las matrices B cuyo producto con A verifique la propiedad conmutativa (AB = BA)
b) Calcula An
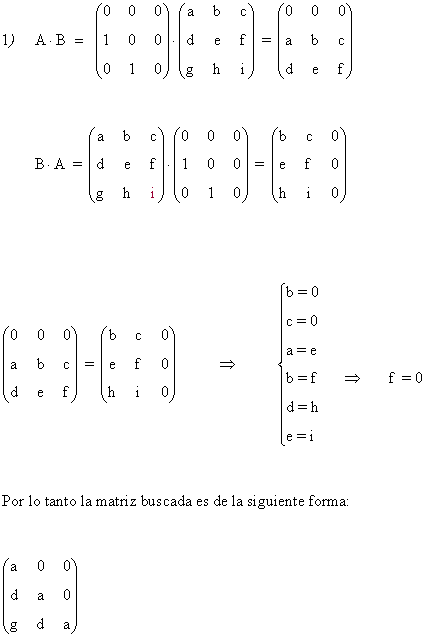
4) Dada la matriz A:
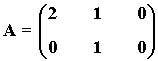
1) Razona si puede existir una matriz B tal que AB = I, siendo I la matriz identidad. En caso afirmativo halla B.
2) ¿Tiene inversa A? Razona la respuesta.
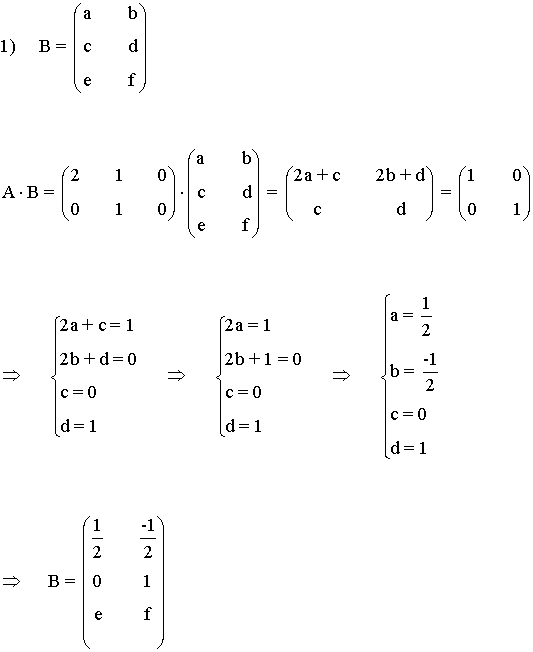
![]()
5) Calcula por el método de Gauss-Jordan la matriz inversa de las siguientes matrices:
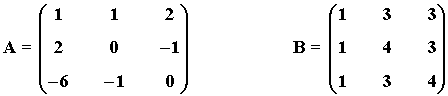
Empezamos calculando la inversa de la matriz A.
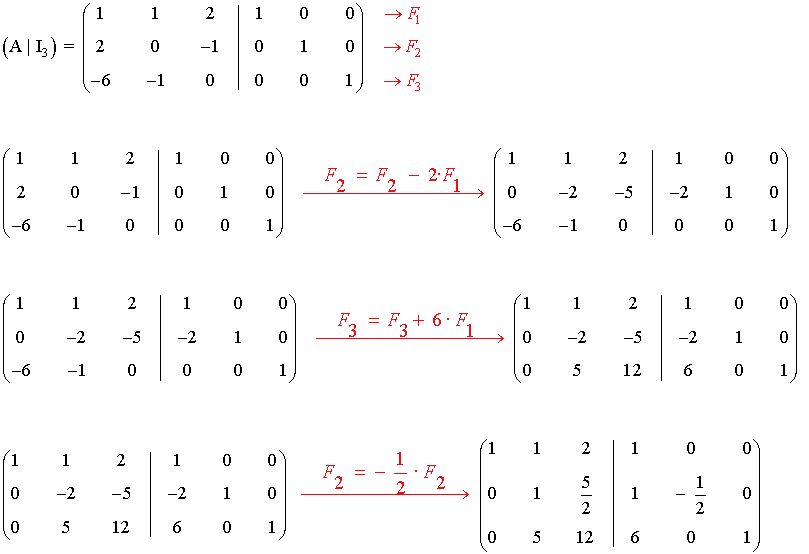
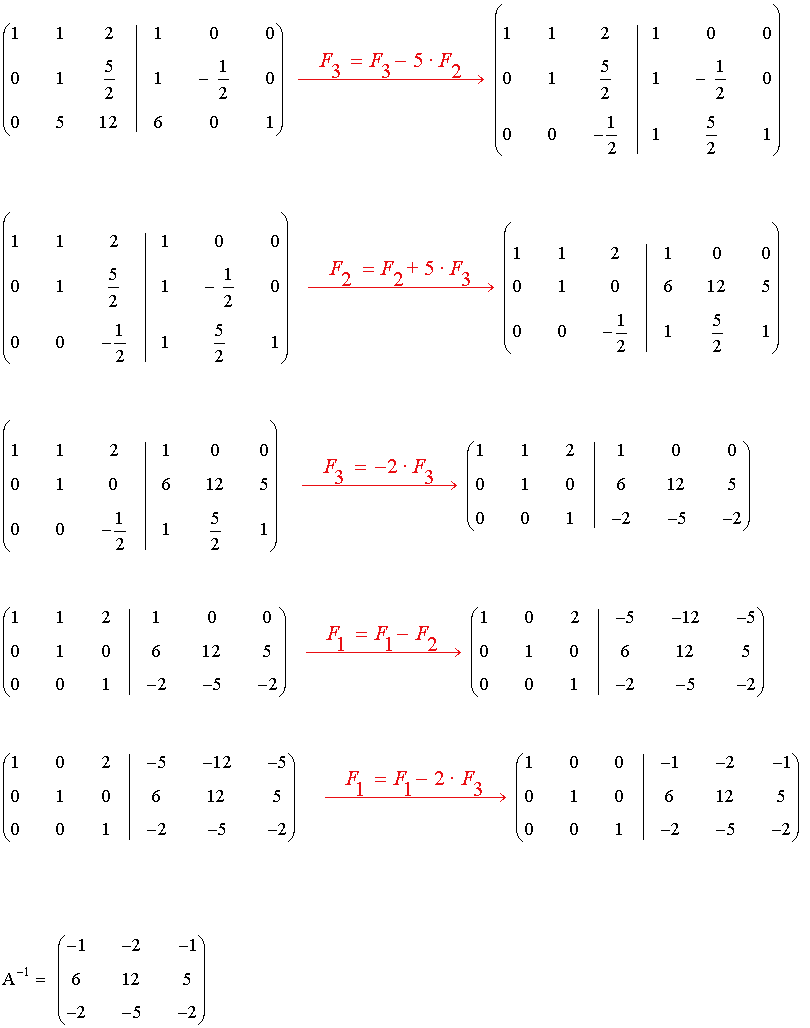
Calculamos ahora la inversa de B
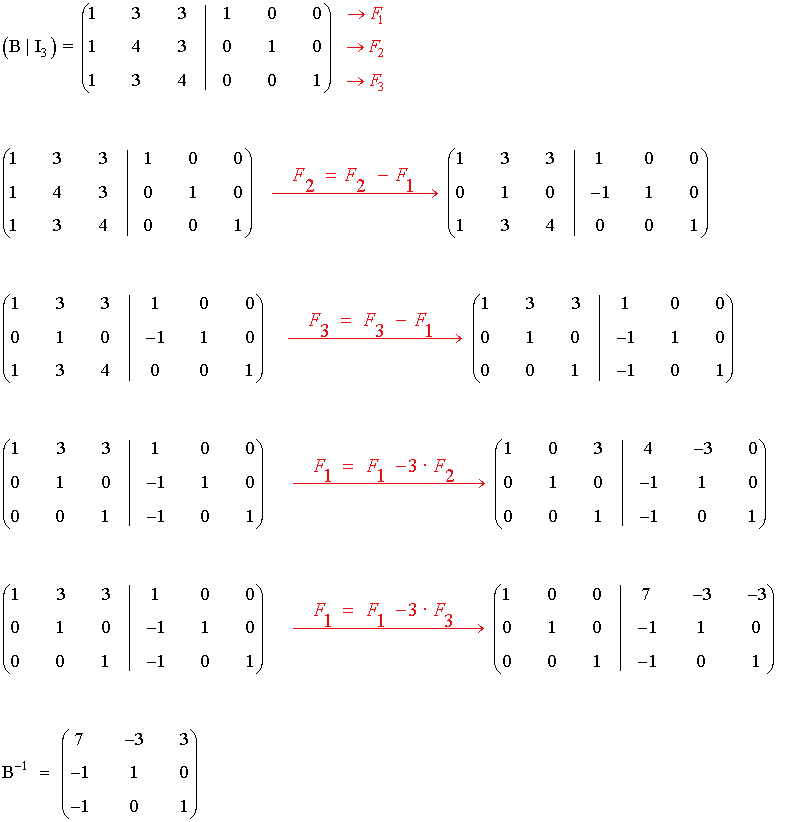
6) Considera la matriz:
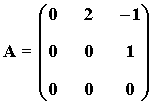
Prueba que B = I + A + A2 es la matriz inversa de I - A , donde I es la matriz identidad de orden 3
Si B es la matriz inversa de (I - A) entonces:
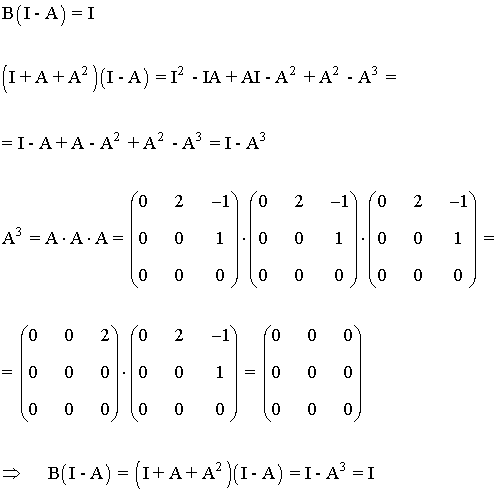
Es decir, B es la matriz inversa de (I - A)
7) Considera la matriz:
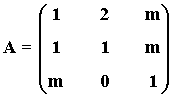
donde m∈IR . Determina para qué valores de m la matriz A es regular (inversible)
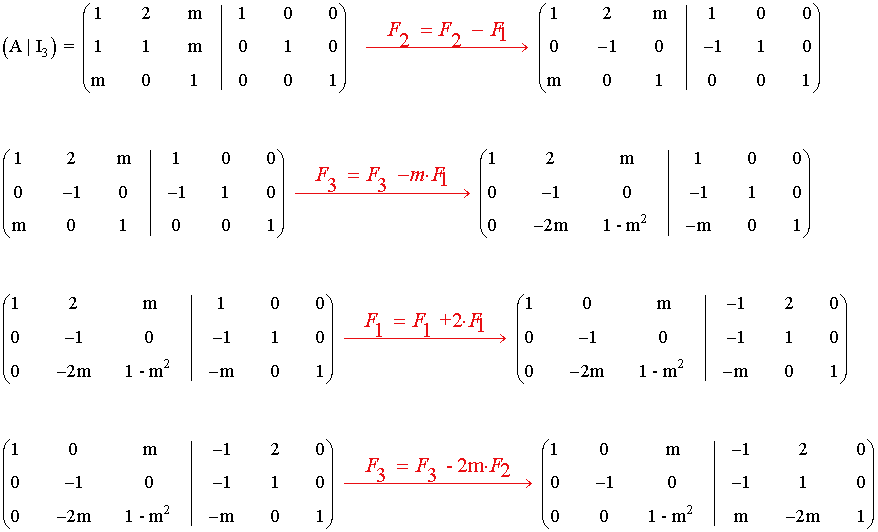
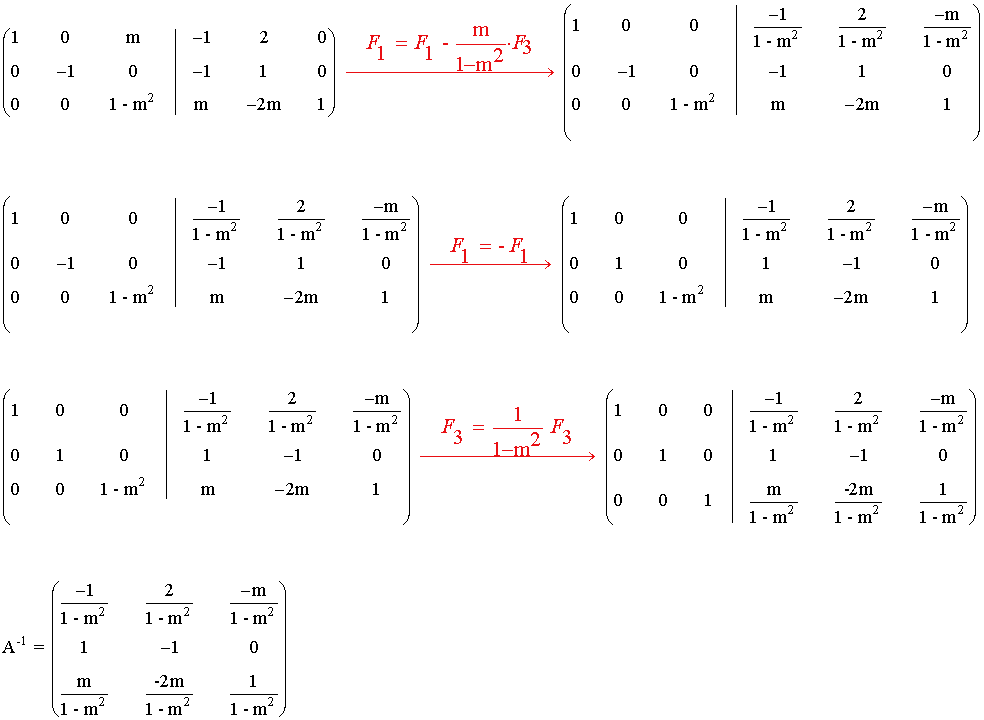
Para poder calcular la inversa tenemos que dividir entre (1 - m2), luego esta expresión no puede ser cero.
Es decir, la matriz A es inversible cuando:
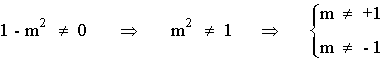
8) Consideremos la matriz A:
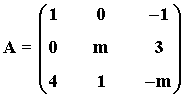
a) Averigua para que valores del parámetro m la matriz no tiene inversa
b) Calcula, si es posible, la matriz inversa de A para m = 2
a) La matriz A tiene inversa si su rango es 3, por lo que transformamos A en una matriz escalonada:
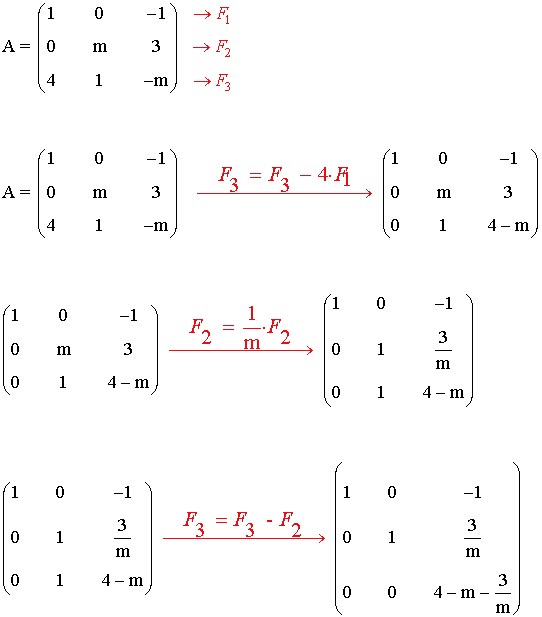
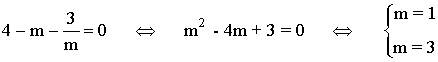
La matriz A no tiene inversa si:
Por lo tanto la matriz A tiene inversa para todo número real m distinto de 1 y 3
b) Para m = 2 la matriz tiene inversa
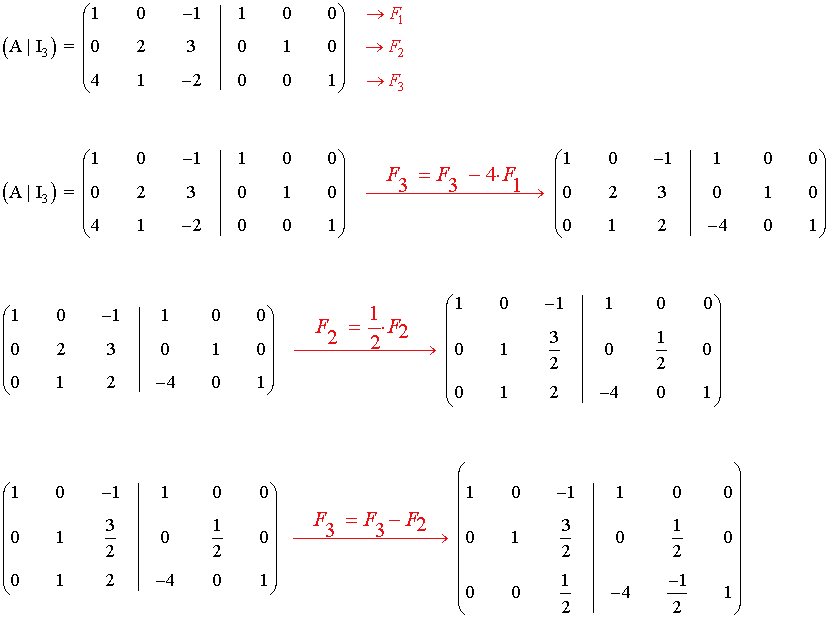
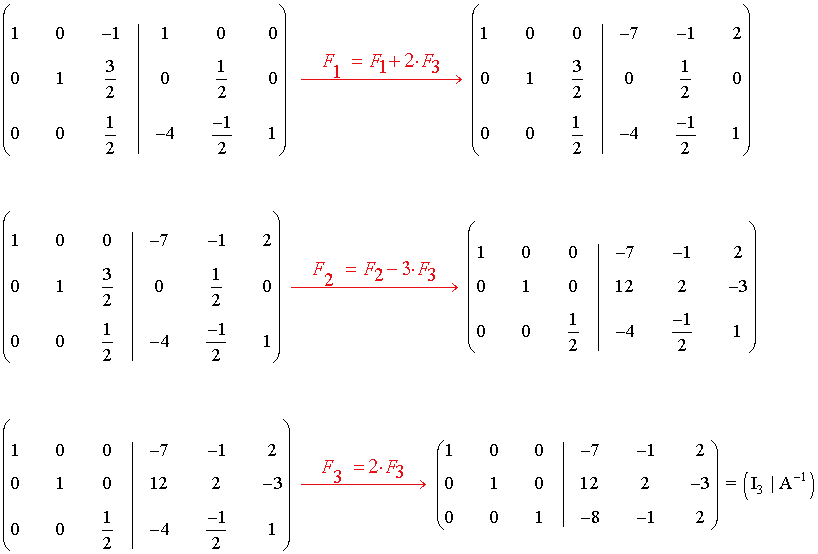
9) Se consideran las matrices:
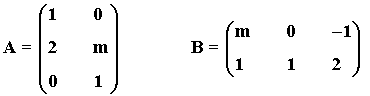
a) Estudia, en función de los valores reales de m , si la matriz B·A tiene inversa
b) Haz lo mismo para la matriz A·B
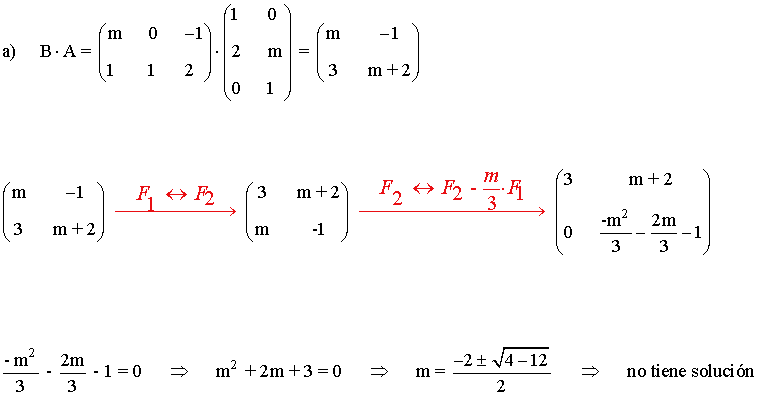
Como no existe ningún valor de m que anule a dicha celda, la matriz B·A siempre tiene rango 2, por lo tanto siempre tiene matriz inversa.

Para cualquier valor de m existe una fila nula en la matriz A·B , es decir, siempre tiene rango 2. Como el rango es menor que la dimensión de la matriz, no existe su matriz inversa sea cual sea el valor de m .
10) Sea la matriz:
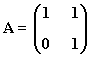
a) Calcular A2 y A3
b) Halla una ley general para calcular An
c) Calcular A10
Aplicamos el método de inducción:
Primer paso: Se calculan las primeras potencias de A:
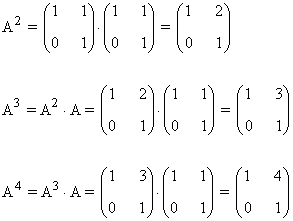
Segundo paso: A partir del resultado anterior, suponemos que:
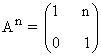
Tercer paso: Se comprueba el resultado para la siguiente potencia An+1
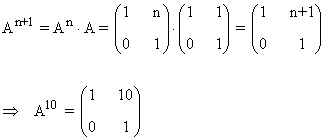
11) Sea la matriz:
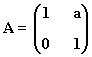
a) Calcula An
b) Halla A22-12A2+2A
Aplicamos el método de inducción:
Primer paso: Se calculan las primeras potencias de A:
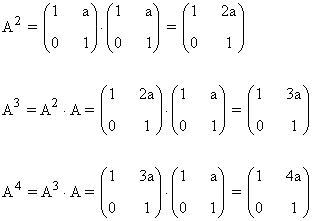
Segundo paso: A partir del resultado anterior, suponemos que:
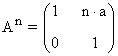
Tercer paso: Se comprueba el resultado para la siguiente potencia An+1
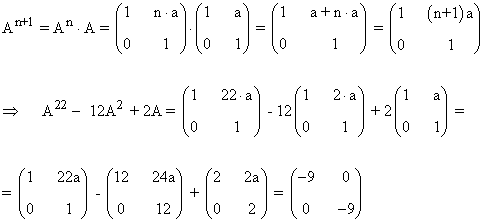
12) Sea la matriz:
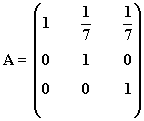
a) Calcula An
b) Halla A35
Aplicamos el método de inducción:
Primer paso: Se calculan las primeras potencias de A:
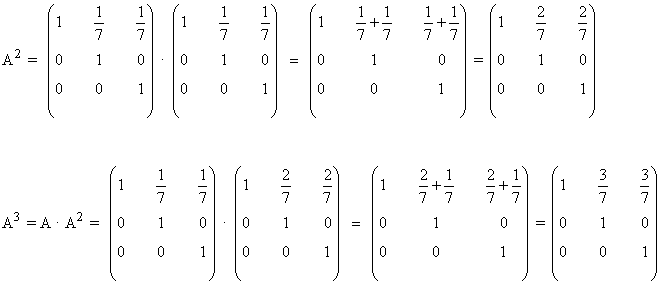
Segundo paso: A partir del resultado anterior, suponemos que:
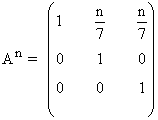
Tercer paso: Se comprueba el resultado para la siguiente potencia An+1
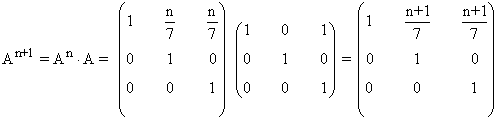
Por lo tanto, hemos demostrado que:
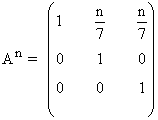
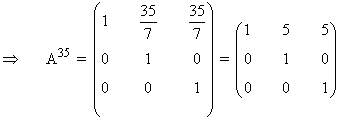
13) Se considerann las siguientes:
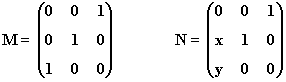
a) Determina x e y para que MN = NM
b) Halla M1995 y M1996
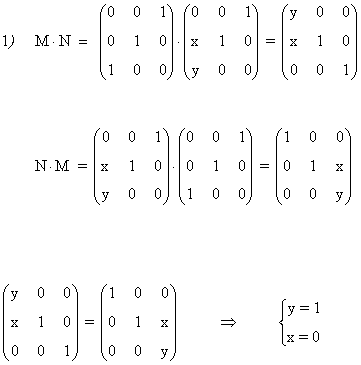
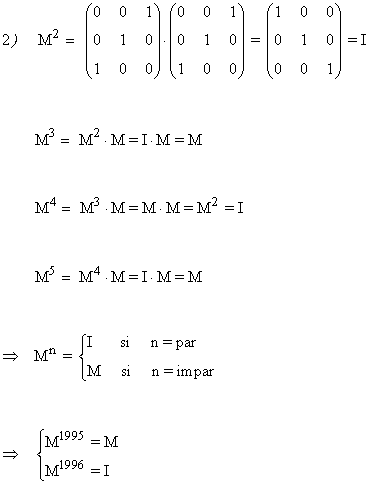
14) Sea la matriz:
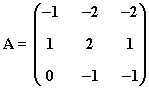
a) Comprueba que verifica que A3 + I = 0
b) Calcula A13
c) Basándote en los apartados anteriores y sin recurrir al cálculo de inversas, halla la matriz X que verifica la igualdad A2X + I = A
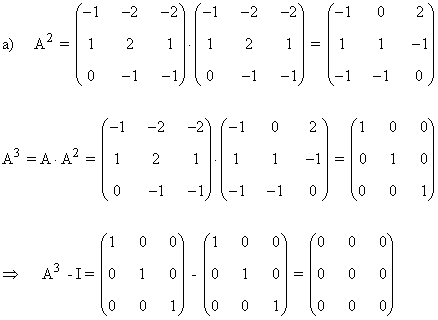
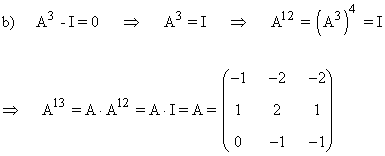
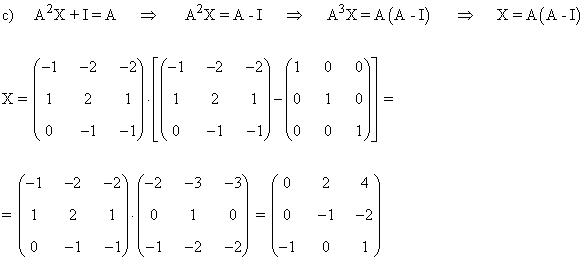
15) Hallar el rango de la matriz B utilizando el método de Gauss:
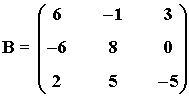
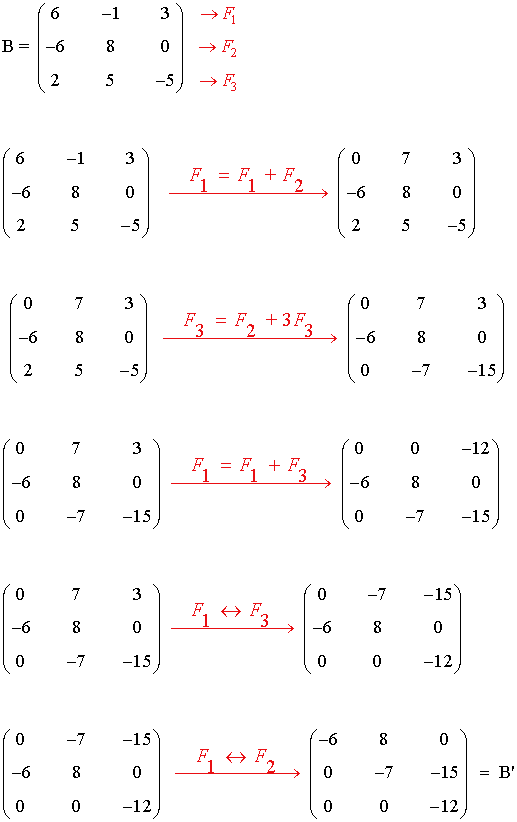
La matriz B' es una matriz escalonada equivalente a B y tiene 3 filas no nulas.
Por tanto rg(B) = 3 .
16) Hallar el rango de la matriz B utilizando el método de Gauss:
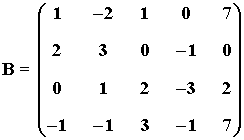

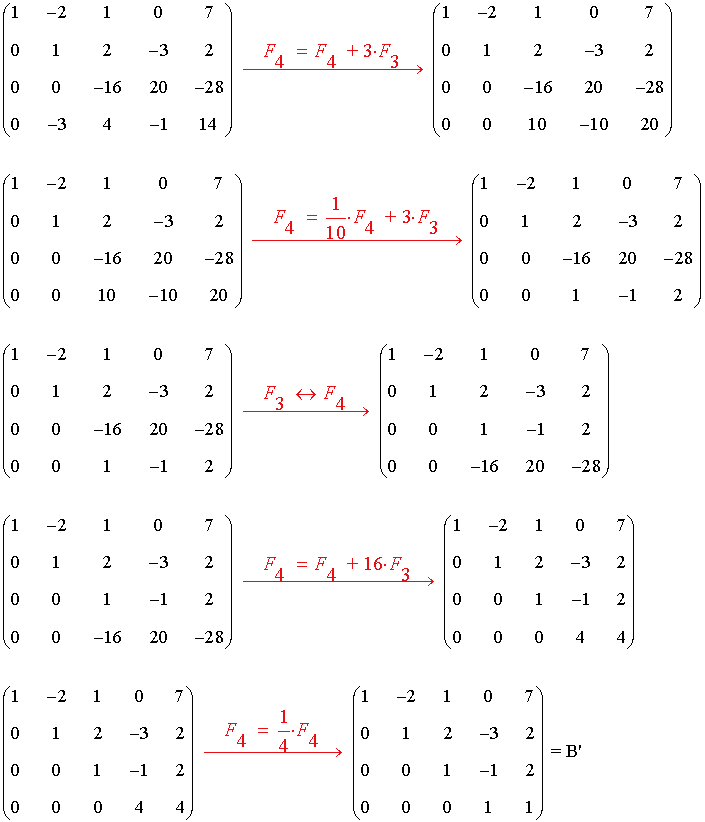
La matriz B' es una matriz escalonada equivalente a B y tiene 4 filas no nulas.
Por tanto rg(B) = 4 .
17) Haz uso del método de Jordan y discute el rango de la matriz A según los valores del parámetro m :
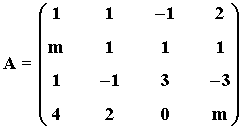
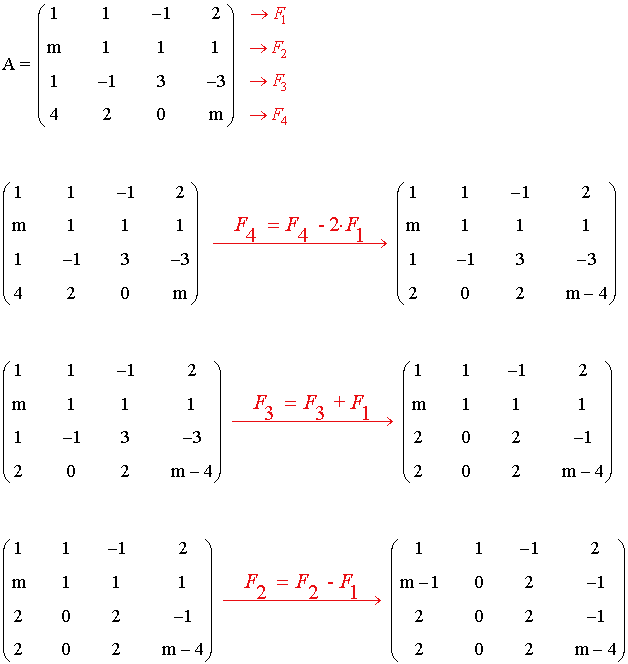
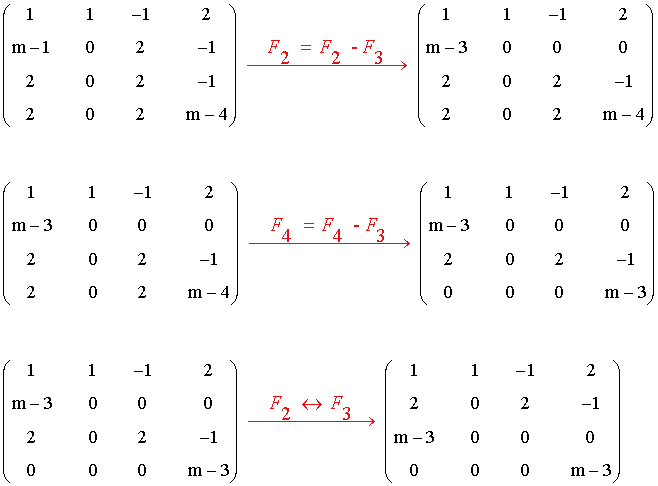
Intercambiando las columnas obtenemos la siguiente matriz escalonada:
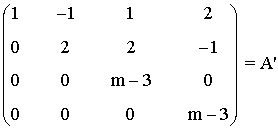
• Si m = 3 ⇒ rg(A) = 2 (dos filas no nulas)
• Si m ≠ 3 ⇒ rg(A) = 4 (cuatro filas no nulas)
18) Dada la siguiente matriz:
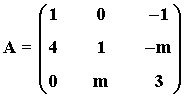
a) Determinar los valores de m para que rango(A) < 3
b) ¿Puede ser rango (A) = 1 para algún valor de m ?
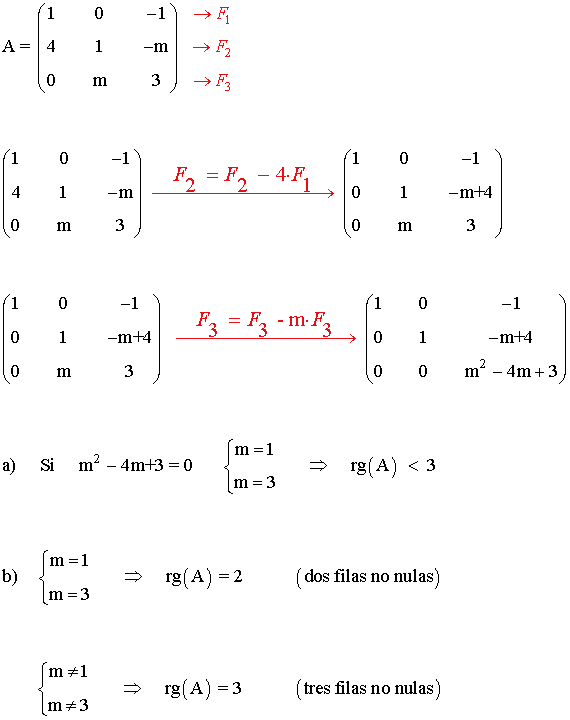
Es decir, el rango de la matriz A no puede ser 1 para ningún valor de m .
19) Dadas las matrices
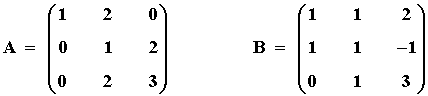
a) Determinar la matriz inversa de B
b) Determinar una matriz X tal que A = B·X
(a)
Empezamos determinando la matriz inversa de B

(b)
Dado que B es una matriz inversible, para encontrar una matriz X tal que se satisfaga la ecuación
A = B · X
bastará con multiplicar por B-1 por la izquierda ambos miembros de la ecuación. De esta forma obtenemos que:
B-1 · A = B-1 · B · X = X
Calculemos ahora la matriz X:
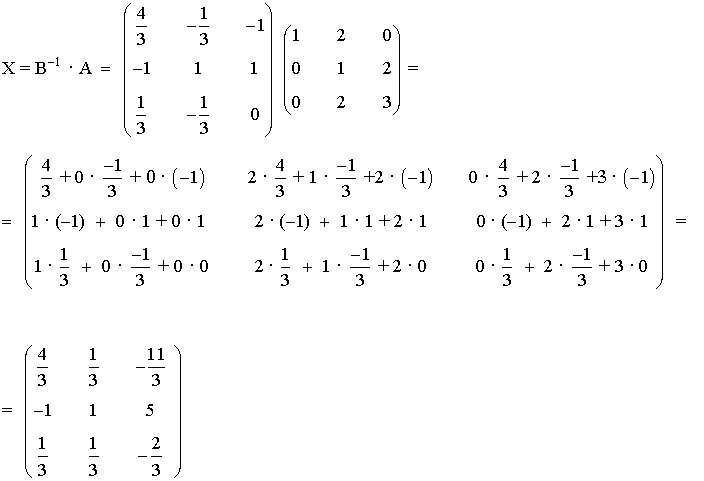
20) Considera las matrices:
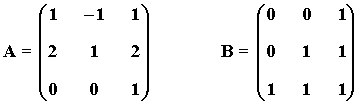
Calcula la matriz X que verifica AX + B = I , donde I representa la matriz identidad.
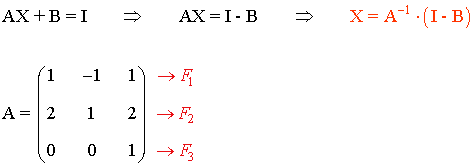
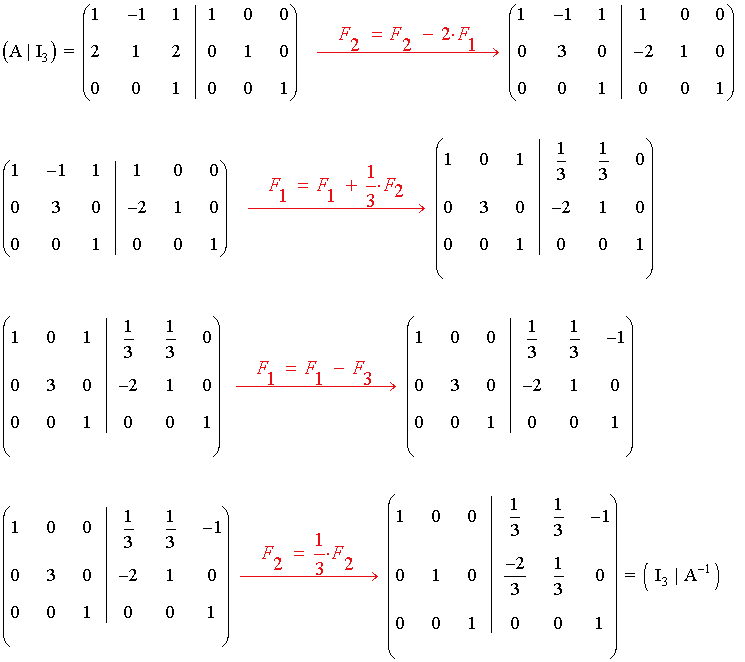
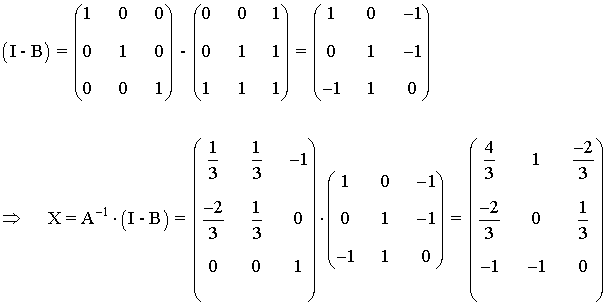
21) Determinar la matriz X en la siguiente ecuación matricial:
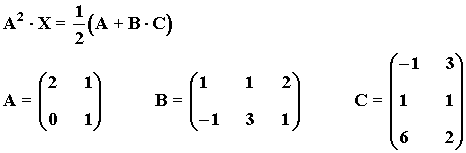
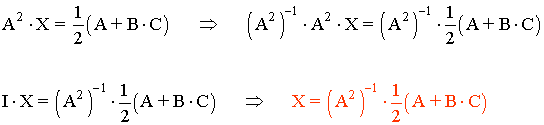
Calculamos por lo tanto la matriz inversa de A2
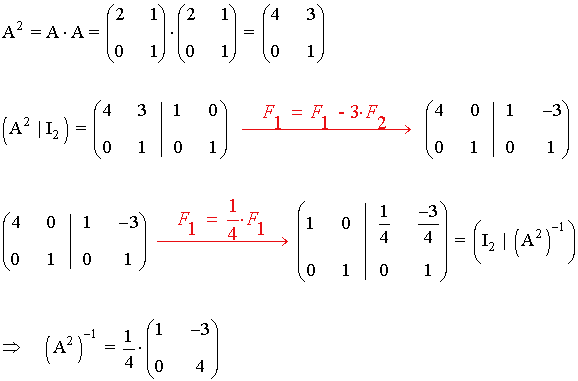
Por otro lado tenemos que:
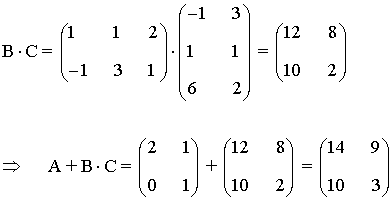
De esta forma podemos calcular X:
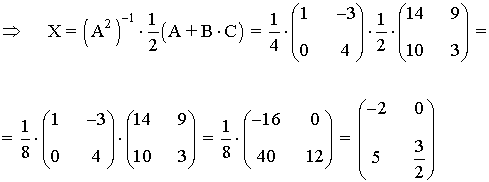
22) Consideremos las siguientes matrices:
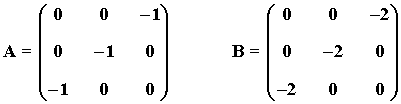
Calcular una matriz cuadrada X sabiendo que verifica X·A2 + B·A = A2
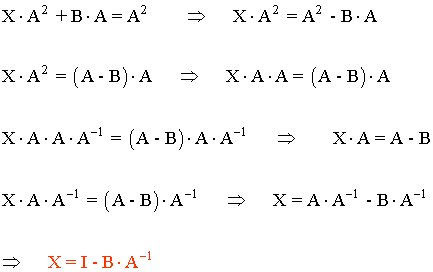
Entre la matriz A y B existe la siguiente relación:
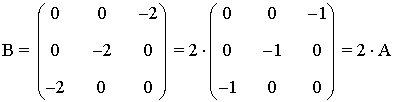
De esta forma podemos calcular X:
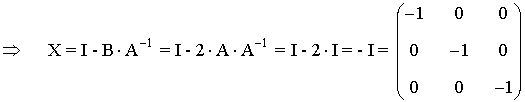
23) Dadas las matrices:
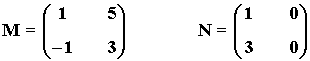
halla dos matrices X e Y que verifiquen:
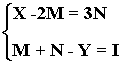
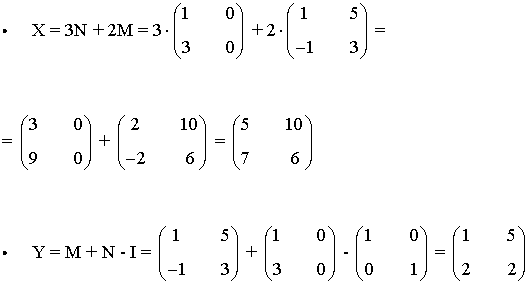
24) Halla las matrices X e Y que verifican el sistema:
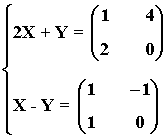
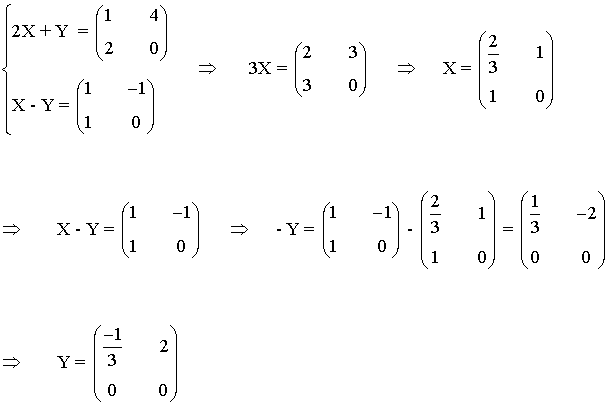
25) Halla dos matrices A y B tales que:
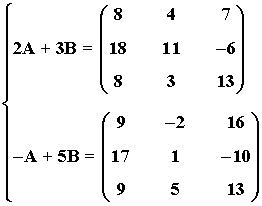
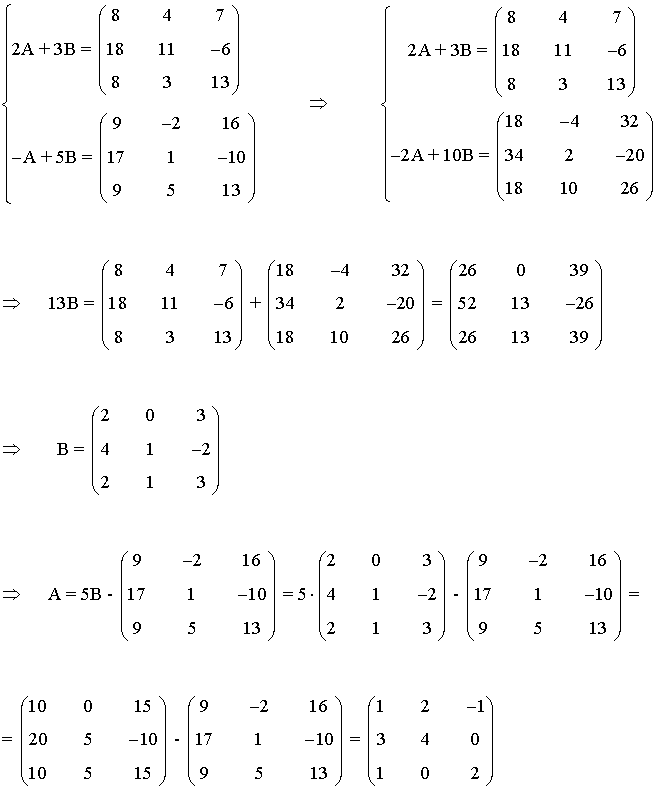


 INICIO
INICIO