Ejercicios resueltos de cálculo de inversa por determinantes
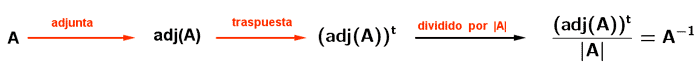
1) Hallar todos los menores complementarios de la matriz A

2) Hallar todos los menores de la matriz A
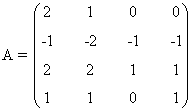
3) Calcula las inversas de las siguientes matrices
y comprueba que los resultados obtenidos son correctos.
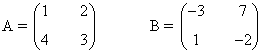
4) Calcula la inversa de la matriz
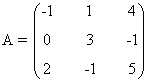
5) Calcula la inversa de la matriz
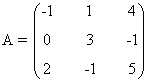
6) Calcula la matriz inversa de:
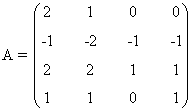
7) ¿Para qué valores de x es la siguiente matriz inversible?
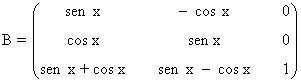
Para dichos valores de x calcula la correspondiente matriz inversa.
8) Halla para qué valores de m admite inversa la matriz siguiente
y calcula dicha inversa para el menor valor entero positivo de m que hace que exista.
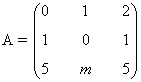
9) Sea la matriz
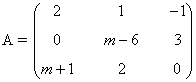
a) Calcule los valores de m para que dicha matriz tenga inversa.
b) Haciendo m = 4, resuelva la ecuación matricial
![]()
10) Sea la matriz

Encuentra su inversa, si existe, cuando a = 1.
11 a) Comprueba que la matriz A cumple que A3 = - A - I
y calcula la matriz inversa de A.
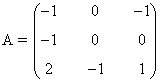
b) Si A es cualquier matriz de n filas y n columnas tal que A3 = - A - I y se sabe que |A|=m,
calcula el valor del determinante de A + I en función de m.
12) Halla los valores de x para los cuales la matriz A:
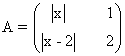
no tiene inversa.
13) Sea la matriz:
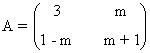
a) Calcule los valores de m para que tenga inversa
b) Haciendo m = 0 resuelva la ecuación matricial A·X·A = I
donde I es la matriz unidad de orden 2 y X una matriz cuadrada de orden 2
14) Estudia para qué valores de m la matriz:
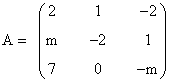
tiene inversa. Halla la matriz A-1 para m = 4
1) Hallar todos los menores complementarios de la matriz A

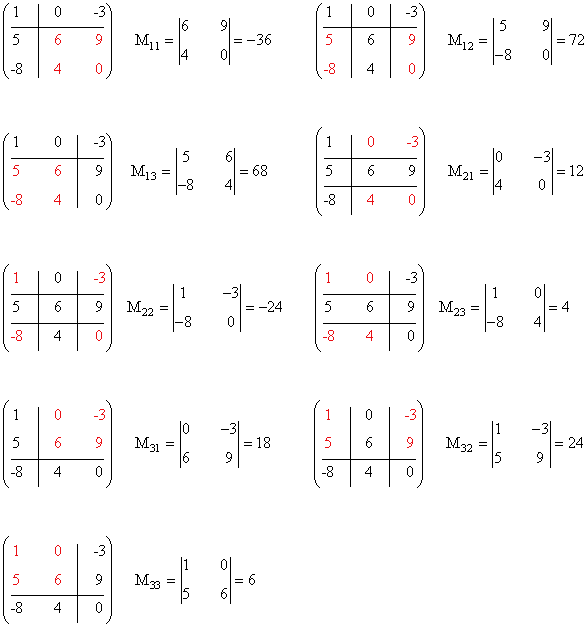
2) Hallar todos los menores de la matriz A
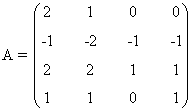
Menores de orden 1:
2, 1, 0, 0, -1, -2, -1, -1, 2, 2, 1, 1, 1, 1, 0, 1
Menores de orden 2:
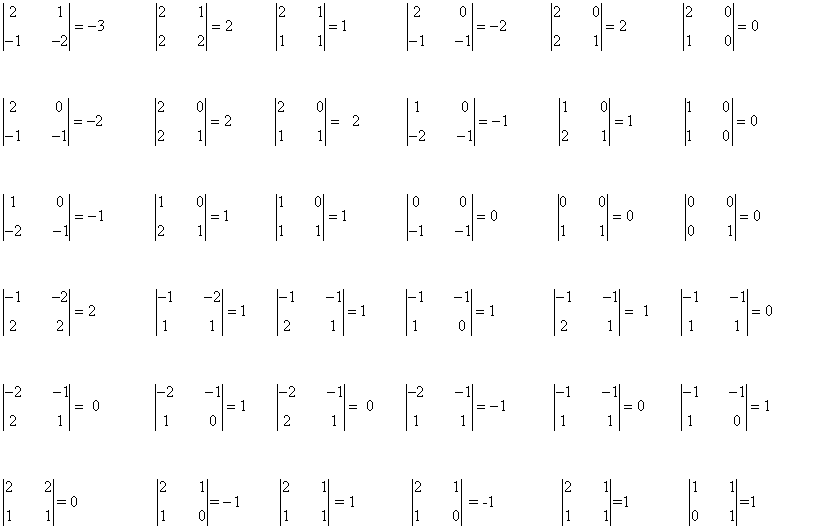
Menores de orden 3:
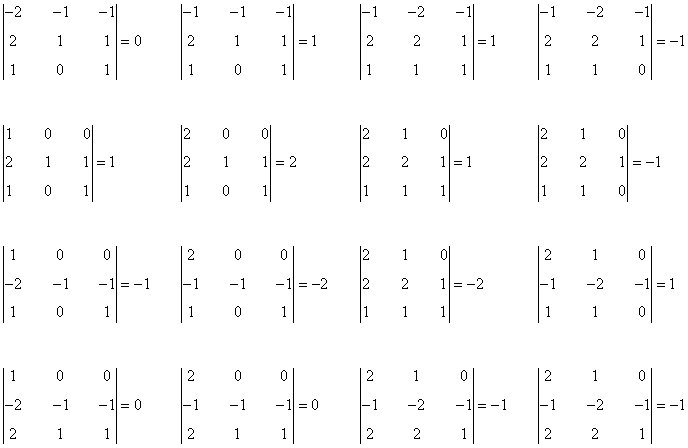
Menor de orden 4:
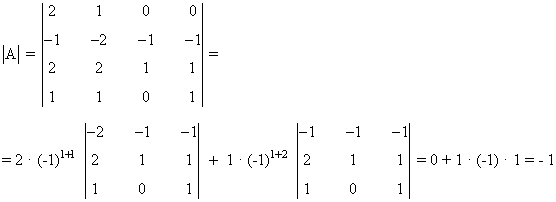
3) Calcula las inversas de las siguientes matrices y comprueba que los resultados obtenidos son correctos.
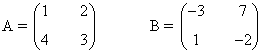
Una matriz es inversible si y sólo si su determinante es no nulo.
Empezamos por la matriz A:
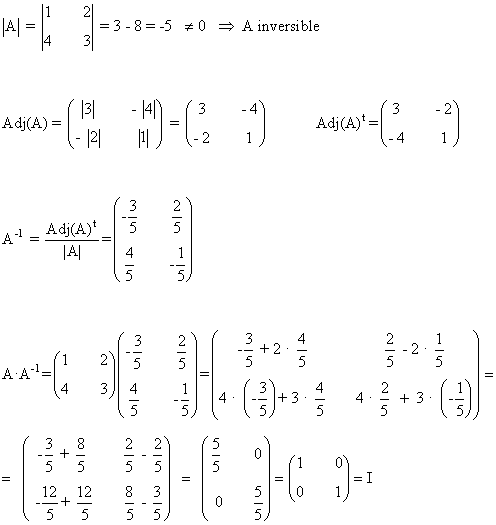
Seguimos y acabamos con la matriz B:
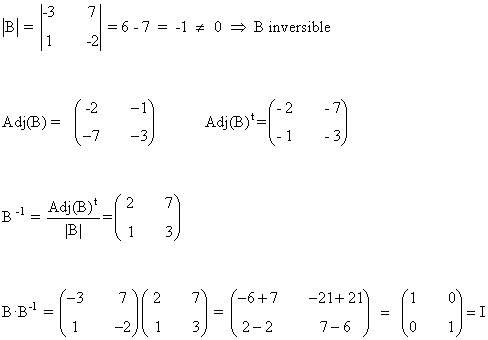
4) Calcula la inversa de la matriz
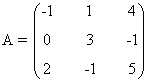
Una matriz es inversible si y sólo si su determinante es no nulo.
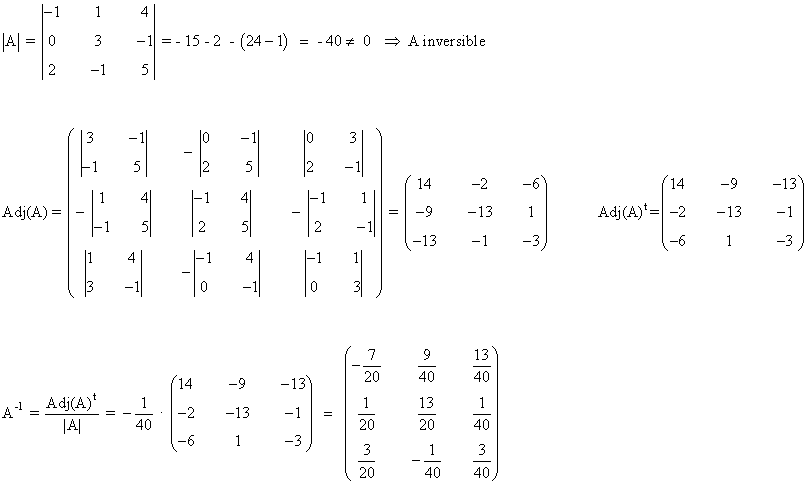
5) Calcula la inversa de la matriz
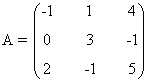
Una matriz es inversible si y sólo si su determinante es no nulo.
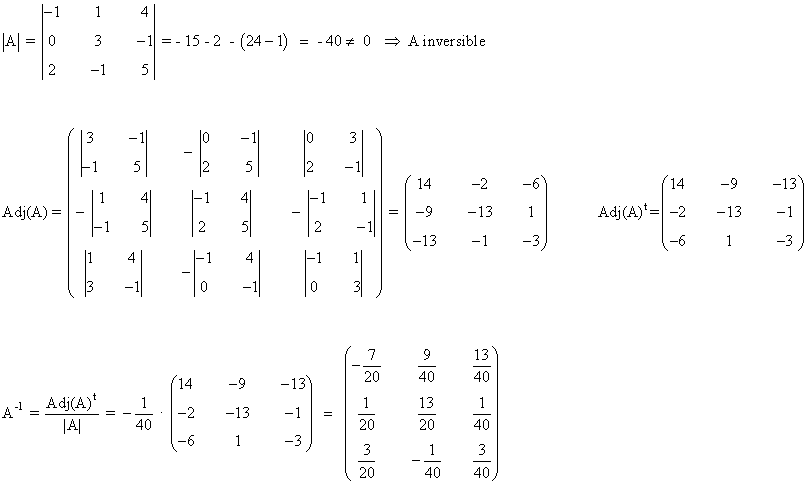
6) Calcula la matriz inversa de:
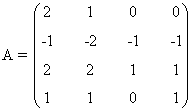
Una matriz es inversible si y sólo si su determinante es no nulo.
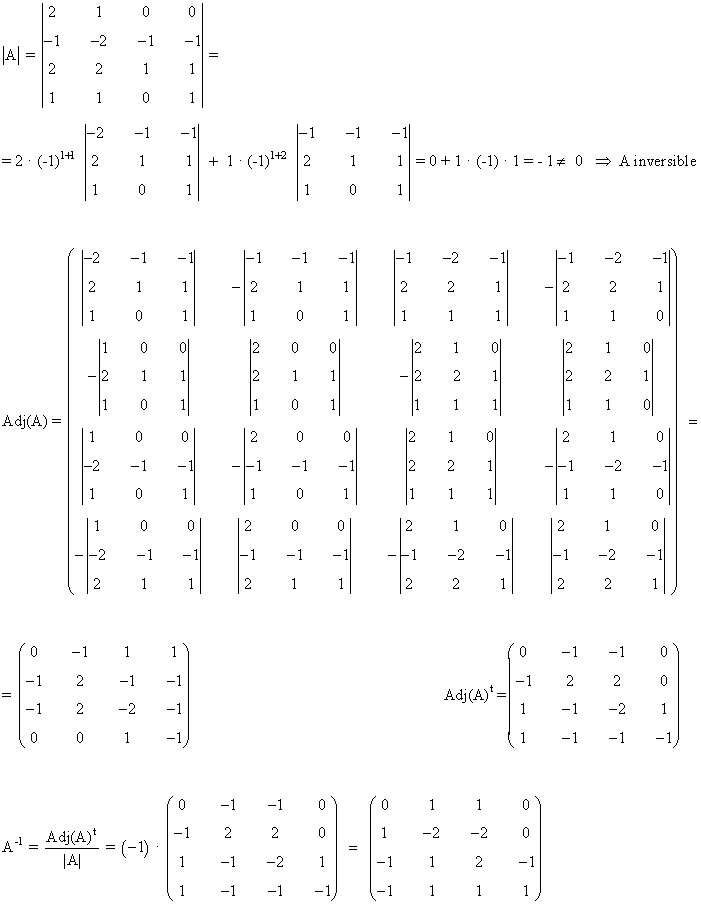
7) ¿Para qué valores de x es la siguiente matriz inversible?
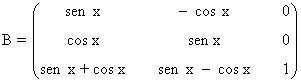
Para dichos valores de x calcula la correspondiente matriz inversa.
Una matriz es inversible si y sólo si su determinante es no nulo.
Vemos que
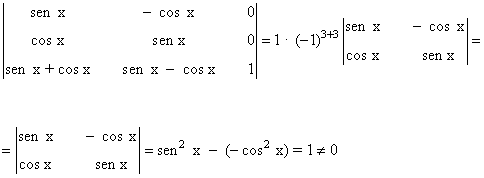
de manera que la matriz B es inversible. Calculamos ahora su inversa:
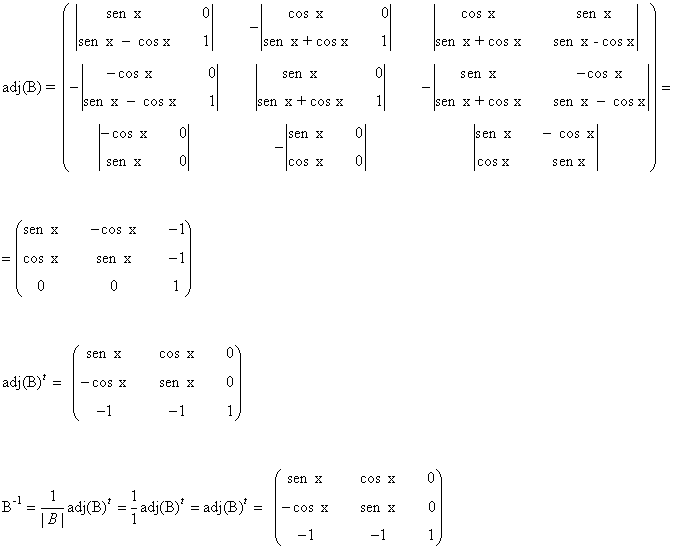
8) Halla para qué valores de m admite inversa la matriz siguiente y calcula dicha inversa para el menor valor entero positivo de m que hace que exista.
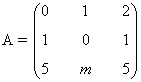
Una matriz es inversible si y sólo si su determinante es no nulo.
Empezamos calculando el determinante de A para averiguar para qué valores de m es la matriz inversible:
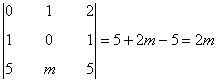
de manera que la matriz A es inversible si y sólo si su determinate es distinto de 0, es decir, si y sólo si m ≠0.
El menor entero positivo para el cual la matriz es inversible es m = 1. Calculamos la inversa de A para m = 1:
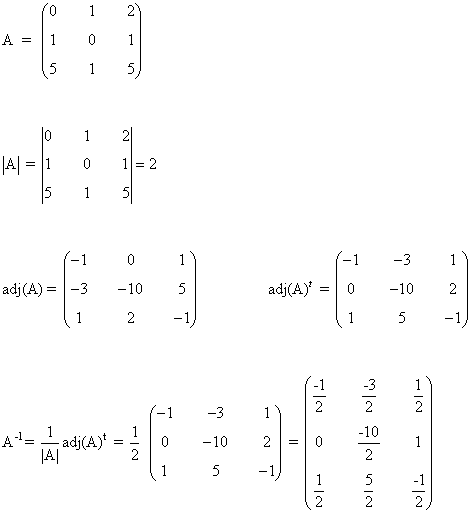
9) Sea la matriz
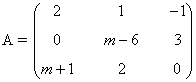
a) Calcule los valores de m para que dicha matriz tenga inversa.
b) Haciendo m = 4, resuelva la ecuación matricial
![]()
Una matriz es inversible si y sólo si su determinante es no nulo.
a)
Bastará con que calculemos el determinante de A y veamos para qué valores de m se anula:
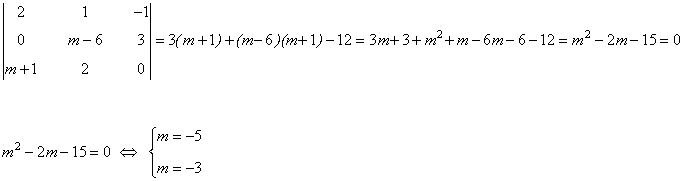
Observamos que A será inversible si y sólo si m≠ -5 y m≠-3.
b)
Si m = 4, por el apartado anterior, A es inversible, de manera que la ecuación que nos piden resolver tiene solución. En efecto, basta multiplicar ambos miembros de la identidad por la derecha por A-1:
X · A = (3 1 1) ⇒
X · A · A-1= (3 1 1) · A-1 ⇒ X = (3 1 1) · A-1
Empezamos calculando la inversa de A:
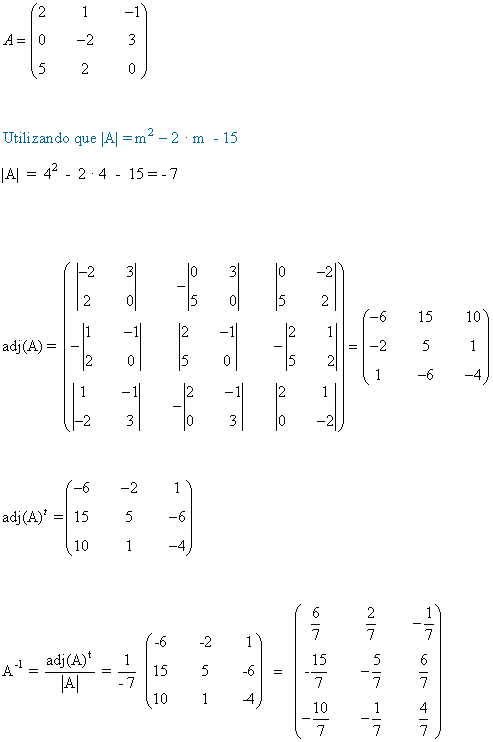
Efectuamos la operación para obtener el valor de X:
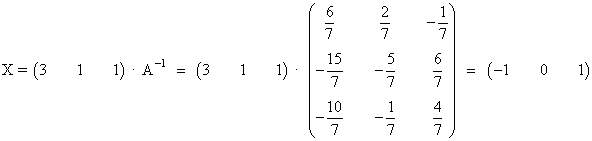
10) Sea la matriz

Encuentra su inversa, si existe, cuando a = 1.
Una matriz es inversible si y sólo si su determinante es no nulo.
Empezamos calculando el determinante de A para averiguar para qué valores de a es la matriz inversible:
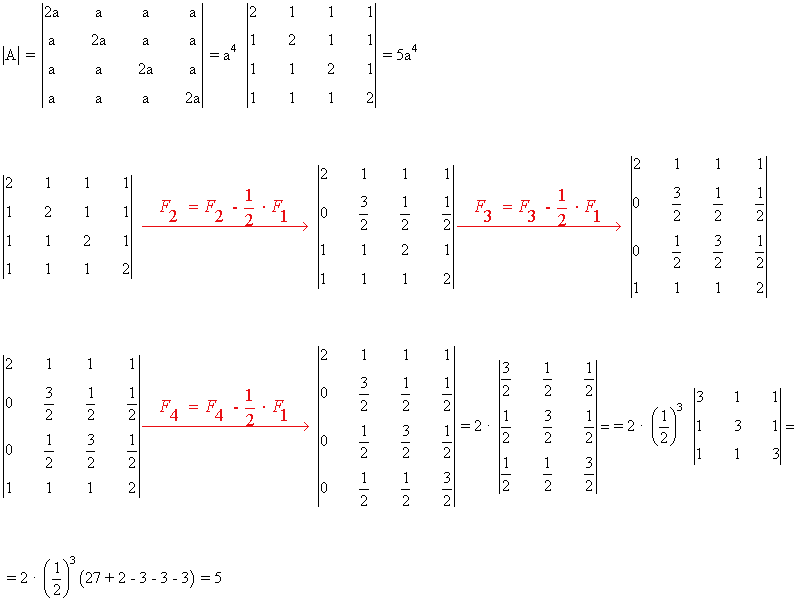
La matriz A será inversible si y sólo si a ≠ 0. Por tanto, para a = 1, A es inversible. Calculemos pues su inversa:
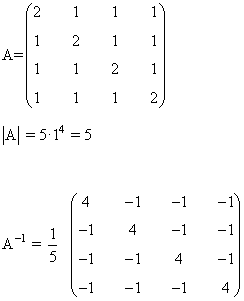
11 a) Comprueba que la matriz A cumple que A3 = - A - I y calcula la matriz inversa de A.
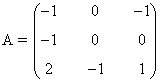
b) Si A es cualquier matriz de n filas y n columnas tal que A3 = - A - I y se sabe que |A|=m, calcula el valor del determinante de A + I en función de m.
(I representa a la matriz identidad)
a)
Calculamos A3:
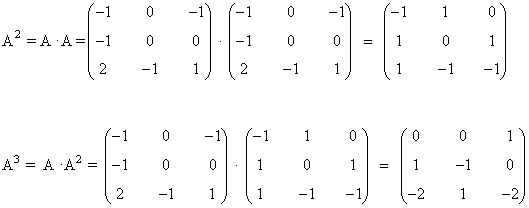
Calculamos - A - I :
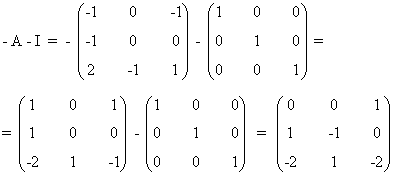
Como puede apreciarse, la identidad A3 = - A - I se verifica.
Para calcular la matriz inversa de A, observamos que
![]()
de manera que A-1 = -A2- I . Calculemos dicha matriz:
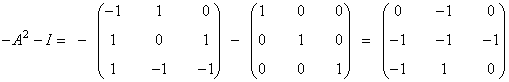
b)
![]()
12) Halla los valores de x para los cuales la matriz A:
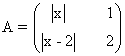
no tiene inversa.
La matriz A no tiene inversa para los valores de x que anulen su determinante: |A| ≠ 0
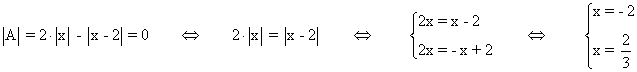
Por lo tanto la matriz A tiene inversa para todo valor real menos para los valores x = -2 y x = 2/3
13) Sea la matriz:
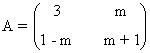
a) Calcule los valores de m para que tenga inversa
b) Haciendo m = 0 resuelva la ecuación matricial A·X·A = I
donde I es la matriz unidad de orden 2 y X una matriz cuadrada de orden 2
a)
Calculamos el determinante de A y lo igualamos a 0:
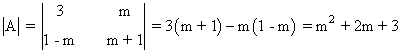
No existe ningún valor de m que verifique la ecuación, por lo que la matriz A tiene inversa para cualquier valor de m.
b)
Resolvemos la ecuación matricial haciendo m = 0
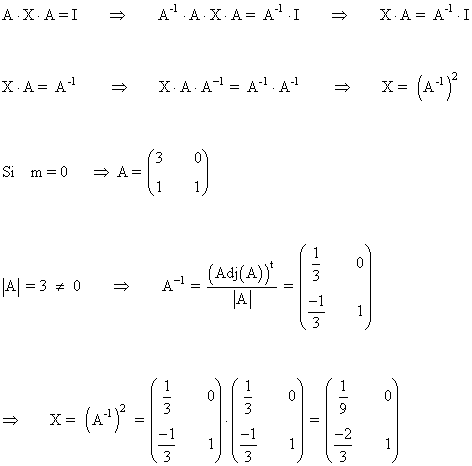
14) Estudia para qué valores de m la matriz:
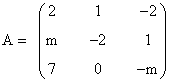
tiene inversa. Halla la matriz A-1 para m = 4
Para que A tenga inversa, tiene que darse que |A| ≠ 0
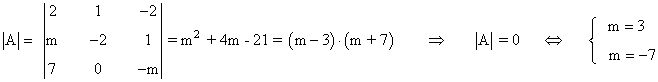
Por lo tanto, la matriz A tiene inversa para cualquier valor de m distinto de 3 y de -7.
Si m = 4 tenemos que:
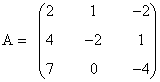
A continuación calculamos su determinante:
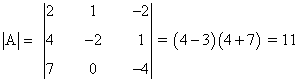
Por otra parte calculamos su matriz adjunta:
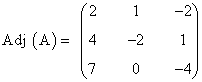
Ahora podemos calcular la matriz inversa:
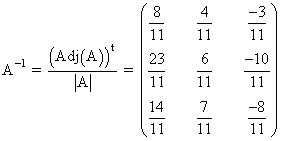


 INICIO
INICIO