Ejercicios resueltos de operaciones de vectores con coordenadas.
Módulo y argumento de vectores.
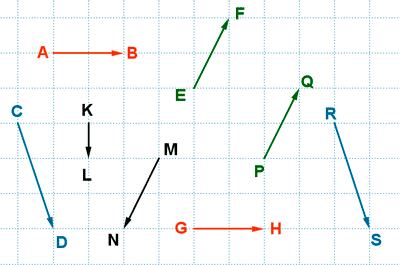
1 - a ) De los siguientes vectores fijos que se muestran en la figura, indica cuáles son equipolentes entre sí y define sus clases.
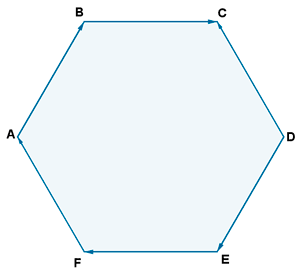
1 - b ) En el hexágono regular de la figura, indica que vectores son equipolentes.
2 ) Los puntos A y B tienen las coordenadas (4, 2) y (2, 5). Halla las coordenadas y el módulo del vector AB.
3 ) Si las coordenadas del vector AB son (2, 5) y las del extremo B(3, -2), halla las coordenadas del origen A.
4 ) Dado los vectores:
![]()
a ) Las coordenadas del punto B, sabiendo que las de A son ( 3 , -1 ) y que el vector AB es equipolente al vector u.
b ) Las coordenadas del punto C, sabiendo que las de D son ( 2 , 3 ) y que el vector CD es equipolente al vector v.
5 ) Dados los siguientes vectores:
![]()
Calcular:
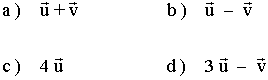
6 ) Dados los siguientes vectores:
![]()
Calcular:
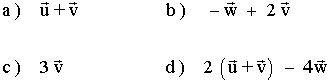
7 ) Calcula el módulo y el argumento de los siguientes vectores:
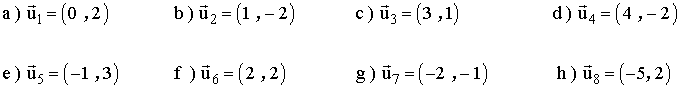
8-a ) ¿ Cómo varía el siguiente módulo si se multiplica por un número real k = 3? Siendo el vector:
![]()
8-b ) Calcula el valor de m para que el vector sea unitario. Siendo dicho vector:
![]()
9 ) Calcula un vector unitario en la misma dirección y sentido que los siguientes:
![]()
10 ) Halla el valor de n para que el argumento α del vector sea el indicado en cada caso.
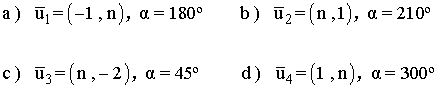
1 - a ) De los siguientes vectores fijos que se muestran en la figura, indica cuáles son equipolentes entre sí y define sus clases.


1 - b ) En el hexágono regular de la figura, indica que vectores son equipolentes.

2 ) Los puntos A y B tienen las coordenadas (4, 2) y (2, 5). Halla las coordenadas y el módulo del vector AB.
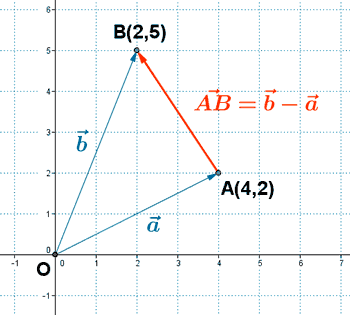
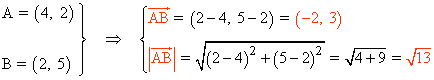
3 ) Si las coordenadas del vector AB son (2, 5) y las del extremo B(3, -2), halla las coordenadas del origen A.
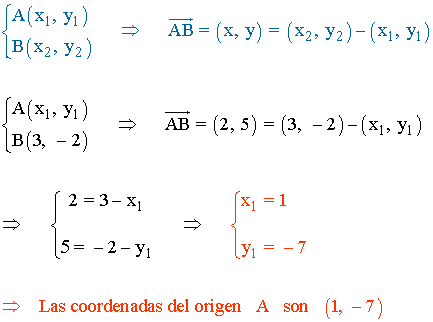
4 ) Dado los vectores:
![]()
a ) Las coordenadas del punto B, sabiendo que las de A son ( 3 , -1 ) y que el vector AB es equipolente al vector u.
b ) Las coordenadas del punto C, sabiendo que las de D son ( 2 , 3 ) y que el vector CD es equipolente al vector v.
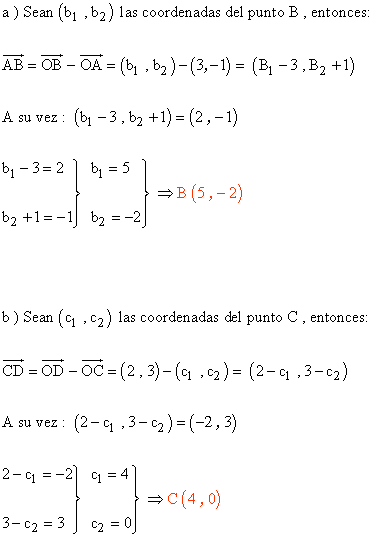
5 ) Dados los siguientes vectores:
![]()
Calcular:
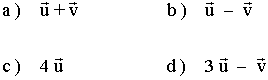
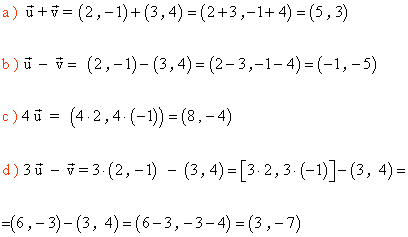
6 ) Dados los siguientes vectores:
![]()
Calcular:
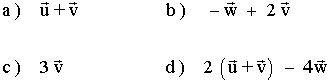
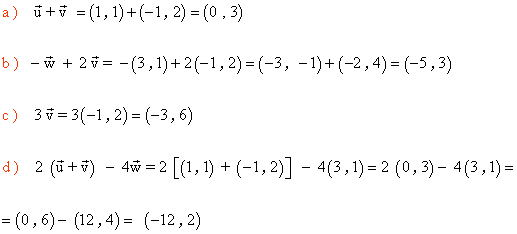
7 ) Calcula el módulo y el argumento de los siguientes vectores:
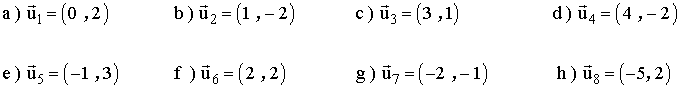

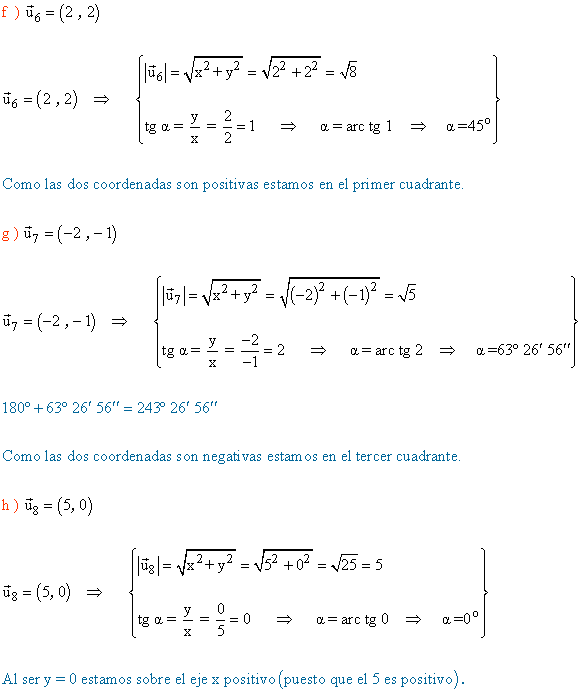
8-a ) ¿ Cómo varía el siguiente módulo si se multiplica por un número real k = 3? Siendo el vector:
![]()
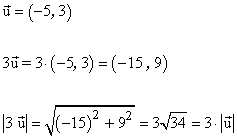
8-b ) Calcula el valor de m para que el vector sea unitario. Siendo dicho vector:
![]()
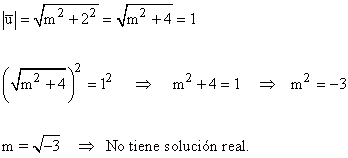
9 ) Calcula un vector unitario en la misma dirección y sentido que los siguientes:
![]()
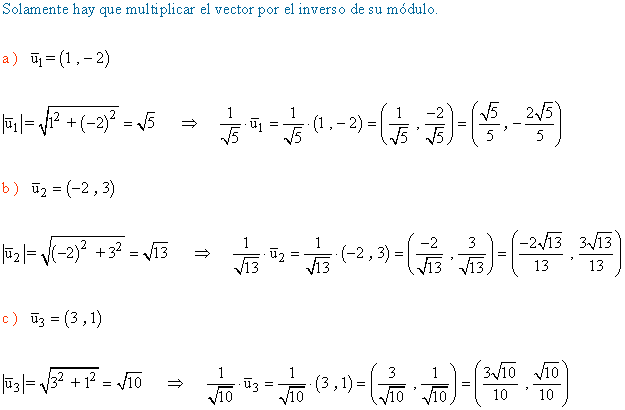
10 ) Halla el valor de n para que el argumento α del vector sea el indicado en cada caso.
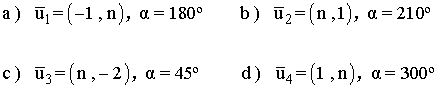
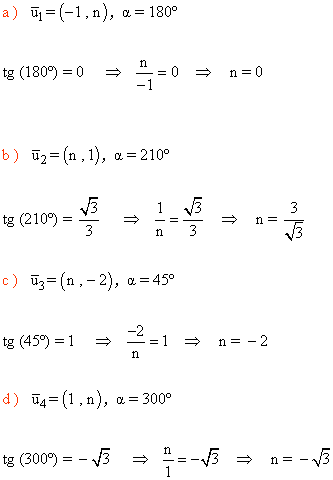


 INICIO
INICIO