Problemas resueltos de optimización III
Figuras planas
| Nombre | Dibujo | Perímetro | Área |
|---|---|---|---|
| Cuadrado |  |
P = 4a | A = a2 |
| Rectángulo |  |
P = 2b + 2a | A = ba |
| Rombo | 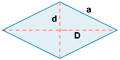 |
P = 4a | |
| Romboide | 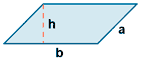 |
P = 2a + 2b | A = b h |
| Trapecio | 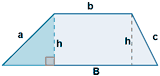 |
P = a + B + b + c | |
| Trapecio isósceles |
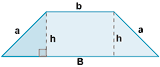 |
P = 2a + B + b | |
| Triángulo | 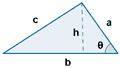 |
P = a + b + c |
|
| Triángulo equilátero |
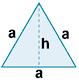 |
P = 3a |
|
| Triángulo rectángulo |
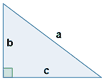 |
P = a + b + c a2 = b2 + c2 |
|
| Hexágono regular |
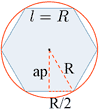 |
P = 6l = 6R ap = apotema |
|
| Pentágono regular |
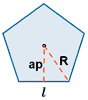 |
P = 5l | ap = apotema |
| Círculo | 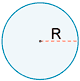 |
L = 2πR | A = πR2 |
| Sector circular |
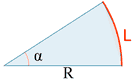 |
L = R α P = 2R + L |
|
| Corona circular |
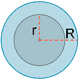 |
L = 2π (R + r) | A = π (R2 - r2) |
| Elipse | 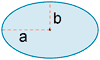 |
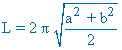 |
A = π a b |
Cuerpos en el espacio
| Dibujo | Área | Volumen | |
|---|---|---|---|
| Cubo | 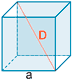 |
A = 6 a2 |
V = a3 |
| Ortoedro |  |
A = 2( a·b + a·c + b·c ) |
V = a · b · c |
| Prisma | 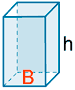 |
PB = perímetro de la base AL = PB · h AT = AL + 2·AB |
V = AB h |
| Pirámide | 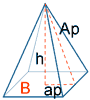 |
PB = perímetro base Ap = apotema pirámide ap = apotema de la base Ap2 = h2 + ap2 AT = AL + AB |
|
| Cilindro | 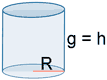 |
AL = 2 π R h AB =2 π R2 AT = 2 π R (h + R) |
V = π R2 h |
| Cono | 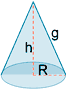 |
g2 = R2 + h2 AL = π R g AB = π R2 AT = π R (g + R) |
|
| Tronco de cono |
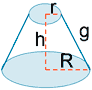 |
AL = π (R + r) g AT = π [ g(R + r) + R2 + r2 ] |
|
| Esfera | 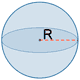 |
A = 4 π R2 | |
| Cuña | 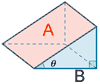 |
A = área cara superior AB = área base A = AB sec θ |
SELECTIVIDAD
Una caja con tapa y base cuadrada debe tener un volumen de 160 cm3. El precio del material utilizado para la base es de 3 euros por centímetro cuadrado y el utilizado para la tapa y los lados es de 2 euros por centímetro cuadrado. Calcular las dimensiones de la caja para que resulte lo más económica posible.
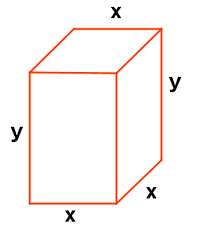
El coste de la caja quedaría definido por la siguiente función:
C = 3x2 + 2x2 + 8xy = 5x2 + 8xy
Por otra parte, sabemos que: x2·y = 160
Es decir, tenemos que:
![]()
Para calcular el coste mínimo, calculamos la primera derivada de la función coste e igualamos a 0:
![]()
![]()
![]()
Para comprobar que el valor corresponde a un mínimo, tenemos que calcular la segunda derivada:
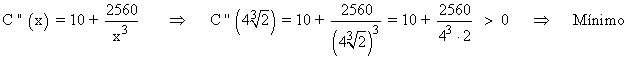
Por lo tanto, las dimensiones de la caja son:
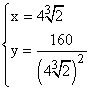
SELECTIVIDAD
Hallar las dimensiones de un depoósito abierto superiormente en forma de prisma recto de base cuadrada, de 50 m3 de volumen, que tenga superficie mínima.
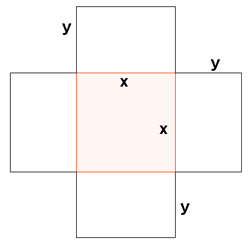
Al tratarse de un prisma recto de base cuadrada tenemos que:
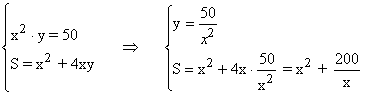
Para calcular la superficie mínima, obtenemos la primera derivada e igualamos a 0:
![]()
Para comprobar que es un mínimo, calculamos la segunda derivada:
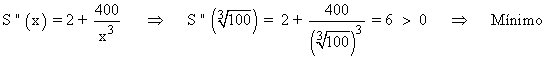
Por lo tanto las dimensiones del depósito son:
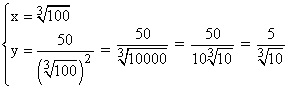
SELECTIVIDAD
Se desea construir una lata de conservas en forma de cilindro circular recto, de área total 150 cm2 y volumen máximo. Determina el radio de la tapa y la altura del cilindro.
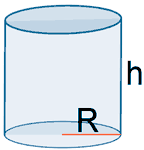
Escribimos las ecuaciones que describen el área total y el volumen de un cilindro:
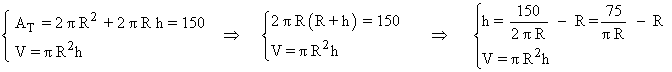
Sustituimos el valor de h en la expresión del volumen:
![]()
Para hallar el valor máximo, calculamos la primera derivada e igualamos a 0:
![]()
Comprobamos que el radio encontrado corresponde con un máximo:
V ''(R) = - 6πR < 0 para cualquier valor de R
Luego el valor de R que hemos encontrado es un máximo. Descartamos la solución negativa ya que geométricamente no tiene sentido.
Hallamos h :
![]()
SELECTIVIDAD
¿Cuál es el volumen máximo que puede tener un cono circular recto de 1 metro de generatriz?
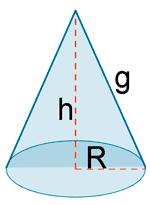
Como la generatriz es 1 metro, por el teorema de Pitagores tenemos que:
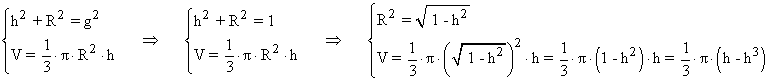
Para calcular el valor máximo, derivamos la función e igualamos a 0:
![]()
Descartamos la solución negativa al no tener sentido geométrico y comprobamos que la solución positiva es un máximo:
![]()
Por lo tanto la solución es:
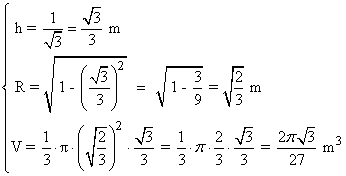
De todos los cilindros inscritos en una esfera de radio 1 metro hallar el volumen del que lo tenga máximo.
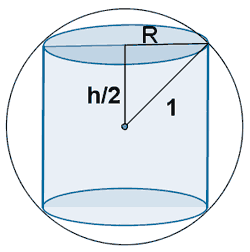
Las condiciones que nos da el problema son las siguientes:
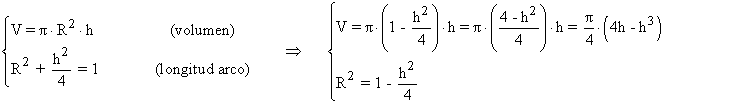
Por lo tanto, para hallar el volumen máximo, derivamos e igualamos a 0:
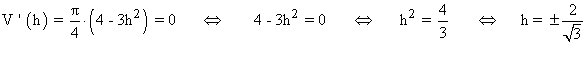
Descartamos la solución negativa puesto que geométricamente no tiene sentido.
A continuación comprobamos que la solución maximiza a la función:
![]()
El volumen máximo pedido es:
![]()
SELECTIVIDAD
Probar que el volumen de cualquier cono recto inscrito en una esfera es menor que el 30% del volumen de la misma.
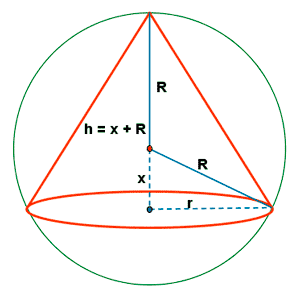
Las condiciones que nos da el problema son las siguientes:

![]()
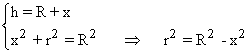
Sustituyendo los valores de h y r2 en la fórmula del volumen del cono, tenemos que:
![]()
Para calcular el volumen máximno derivamos e igualamos a 0:
![]()
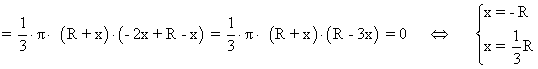
Para comprobar si las soluciones son máximo o mínimo, calculamos la segunda derivada:
![]()
![]()
![]()
Por lo tanto, el volumen máximo del cono inscrito en la esfera es:
![]()
Como el volumen de la esfera es:
![]()
Tenemos por tanto que:
![]()
SELECTIVIDAD
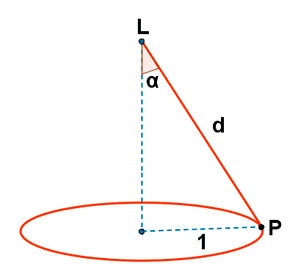
Para iluminar una mesa circular de un metro de radio, se suspende del techo de la habitación un foco de luz situado en la vertical del centro de la mesa y que enfoque hacia abajo. Decir a que altura debe situarse este foco respecto a la mesa para que los puntos de su borde tengan una iluminación máxima. Si designamos por L el foco (que se considera puntual) y por P un punto cualquiera de la mesa, la iluminación I del punto P viene dada por:
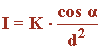
donde K es una constante que depende de las características del foco, d es la distancia entre P y L, y α es el ángulo entre PL y la vertical.
Sabemos que:
![]()
Por lo tanto, la fórmula de la iluminación sería:
![]()
Hallamos la derivada e igualamos a 0:
![]()
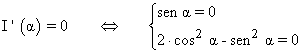
Buscamos las soluciones de ambas ecuaciones:
![]()
![]()
De las tres soluciones, la única físicamente posible es: α = arc tg √2 ≈ 54,73º

A continuación calculamos la altura:
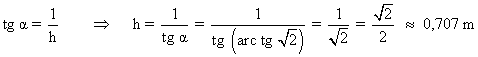
SELECTIVIDAD
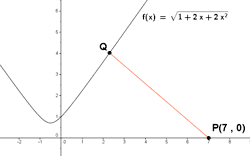
Desde una casa situada en el punto P(7 , 0) se quiere hacer un camino recto para conectarla con una carretera cuyo trazado viene dado por la curva de ecuación:
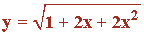
¿Con qué punto de la carretera conecta el camino más corto posible?
La distancia entre dos puntos P(x1, y1) y Q(x2, y2) viene dada por la siguiente fórmula:
![]()
Llamemos Q=(x , y) al punto de la curva más cercano a p.
La ecuación que relaciona ambas coordenadas viene dada por la función:
![]()
Y la expresión que describe la distancia entre ambos puntos:
![]()
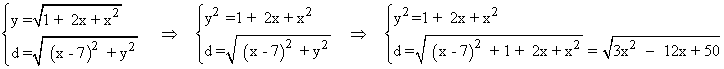
Para encontrar el mínimo de la función distancia calculamos su derivada e igualamos a 0:
![]()
Para confirmar que x = 2 corresponde a un mínimo, calculamos el signo de la primera derivada antes y despues de dicho punto :

Luego la coordenada de abscisa que minimiza la distancia es x = 2.
Si x = 2 ⇒ y = √13
El punto buscado es: Q = (2 , √13)
SELECTIVIDAD
Dada la función f(x) = 1/x
a) Hallar la ecuación de la recta tangente a su gráfica en el punto (a, f(a)) para a > 0
b) Hallar los puntos de corte de la recta tangente hallada en el apartado a) con los dos ejes coordenados
c) Hallar el valor de a > 0 que hace que la distancia entre los dos puntos hallados en b) sea mínima.
a) Determinación de la ecuación:
La recta tangente a una función viene determinada por:
![]()
Por otro lado tenemos que:
![]()
Por lo tanto, la recta tangente en un punto x = a viene determinada por:
![]()
b) Puntos de corte:
![]()
![]()
c) Optimización:
La distancia entre dos puntos P(x1, y1) y Q(x2, y2) viene dada por la siguiente fórmula:
![]()
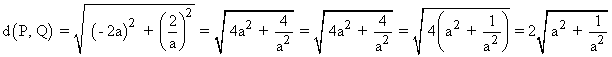
Por tanto, tenemos que optimizar la siguiente función:
![]()
Calculamos la primera derivada e igualamos a 0:
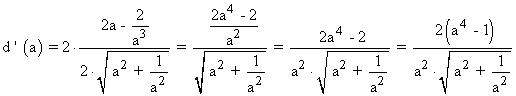
![]()
Como en el enunciado nos piden que a > 0 , el único punto que nos interesa es a = 1 .
Para confirmar que corresponde a un mínimo, calculamos el signo de la primera derivada antes y despues de a = 1 :
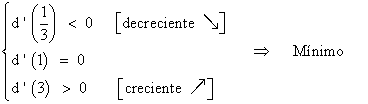
SELECTIVIDAD
Considera el recinto limitado por la siguiente curva y la siguiente recta:

De entre todos los rectángulos situados como el de la figura, determina el que tiene área máxima.
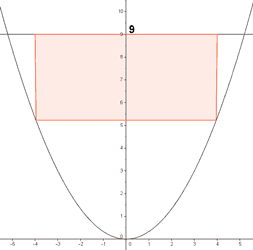
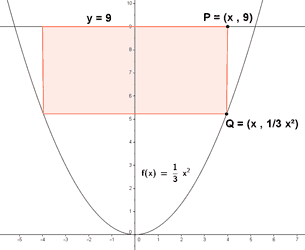
Observamos que la base es 2x , y la altura es la diferencia de la función de arriba y la de abajo: h = 9 - 1/3 x2
Escribimos la función área del rectángulo:
![]()
Para encontrar el máximo de la función área calculamos su derivada y la igualamos a 0:
![]()
h = 9 - 1/3 (±3)2 = 9 - 3 = 6
Comprobamos qué solución es máximo: A ''(x) = -4x
• A''(-3) = 12 > 0 es mínimo
• A''(3) = -12 < 0 es máximo
Luego las dimensiones del rectángulo son 6 unidades de alto y 6 unidades de ancho.


 INICIO
INICIO