Problemas resueltos de optimización II
Figuras planas
| Nombre | Dibujo | Perímetro | Área |
|---|---|---|---|
| Cuadrado |  |
P = 4a | A = a2 |
| Rectángulo |  |
P = 2b + 2a | A = ba |
| Rombo | 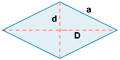 |
P = 4a | |
| Romboide | 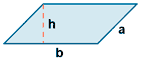 |
P = 2a + 2b | A = b h |
| Trapecio | 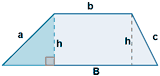 |
P = a + B + b + c | |
| Trapecio isósceles |
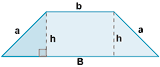 |
P = 2a + B + b | |
| Triángulo | 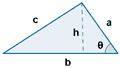 |
P = a + b + c |
|
| Triángulo equilátero |
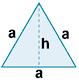 |
P = 3a |
|
| Triángulo rectángulo |
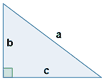 |
P = a + b + c a2 = b2 + c2 |
|
| Hexágono regular |
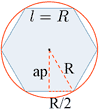 |
P = 6l = 6R ap = apotema |
|
| Pentágono regular |
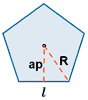 |
P = 5l | ap = apotema |
| Círculo | 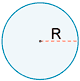 |
L = 2πR | A = πR2 |
| Sector circular |
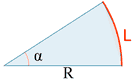 |
L = R α P = 2R + L |
|
| Corona circular |
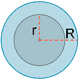 |
L = 2π (R + r) | A = π (R2 - r2) |
| Elipse | 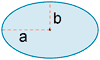 |
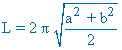 |
A = π a b |
Cuerpos en el espacio
| Dibujo | Área | Volumen | |
|---|---|---|---|
| Cubo | 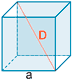 |
A = 6 a2 |
V = a3 |
| Ortoedro | 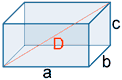 |
A = 2( a·b + a·c + b·c ) |
V = a · b · c |
| Prisma | 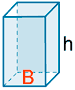 |
PB = perímetro de la base AL = PB · h AT = AL + 2·AB |
V = AB h |
| Pirámide | 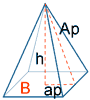 |
PB = perímetro base Ap = apotema pirámide ap = apotema de la base Ap2 = h2 + ap2 AT = AL + AB |
|
| Cilindro | 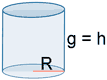 |
AL = 2 π R h AB =2 π R2 AT = 2 π R (h + R) |
V = π R2 h |
| Cono | 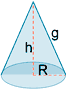 |
g2 = R2 + h2 AL = π R g AB = π R2 AT = π R (g + R) |
|
| Tronco de cono |
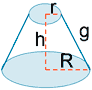 |
AL = π (R + r) g AT = π [ g(R + r) + R2 + r2 ] |
|
| Esfera |  |
A = 4 π R2 | |
| Cuña |  |
A = área cara superior AB = área base A = AB sec θ |
SELECTIVIDAD
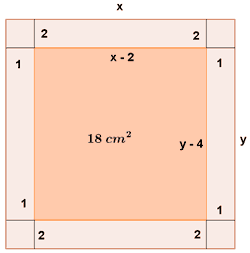
Una hoja de papel debe tener 18 cm2 de texto impreso, márgenes superior e inferior de 2 cm de altura y márgenes laterales de 1 cm de altura. Obtener razonadamente las dimensiones que minimizan la superficie de papel.
1) Para resolver un problema de optimización debemos encontrar una función a la que calcularle sus extremos (máximos o mínimos).
Por lo tanto tenemos que localizar las variables que definan la función que queremos optimizar.
En nuestro caso las variables que definen a la superficie corresponden al ancho (x) y alto (y) del papel:
S = x · y
Y la relación entre ambas variables es:
(x - 2) · (y - 4) = 18
A continuación operamos y despejamos una de ellas en función de la otra:
xy - 4x - 2y + 8 = 18
y(x - 2) - 4x = 10
Despejando obtenemos la siguiente función:
![]()
2) Calculamos la primera derivada y la igualamos a 0:
![]()
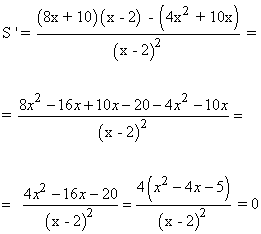
Es decir, tenemos que resolver la siguiente ecuación: x2 - 4x - 5 = 0
Los raíces de la ecuación de segundo grado son x = 5 y x = - 1 (esta solución la desechamos porque no existen distancias negativas).
Comprobamos que para x = 5 la función tiene un mínimo:
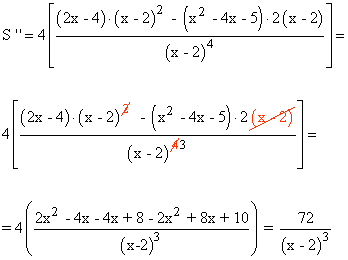
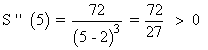
3) Calculamos las imágenes de los extremos:
![]()
Se considera una ventana rectangular en la que el lado superior ha sido sustituido por un triángulo equilátero tal y como se indica en la figura. Sabiendo que el perímetro de la ventana es de 6,6 metros, hallar sus dimensiones para que su superficie sea máxima.
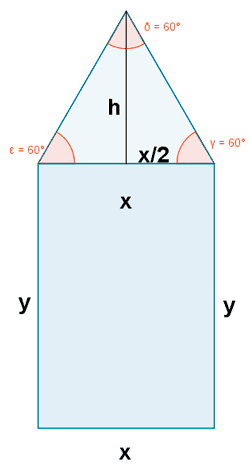
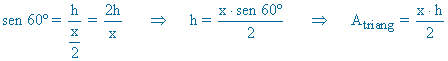
Como el lado superior es un triángulo equilátero, sus lados miden lo mismo que la base del rectángulo, siendo su altura:
Por lo tanto, a partir de las condiciones del problema, tenemos que el perímetro y la superficie son:
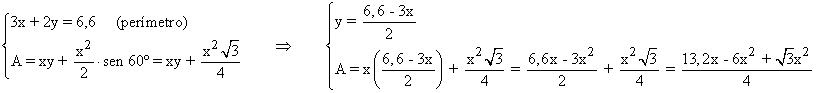
Calculamos la primera derivada de la función obtenida e igualamos a 0:
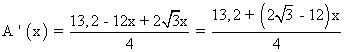
![]()
![]()
Por lo tanto, las dimensiones son las siguientes:
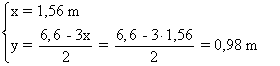
Determina las dimensiones de una puerta formada por un rectángulo y un semicírculo (como en la figura), sabiendo que es la que tiene perímetro mínimo entre las que tienen área igual a 2 m2 .
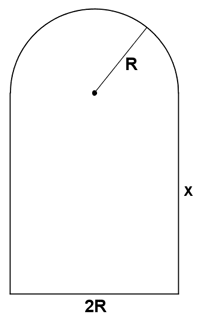
Las condiciones que nos determina el problema son las siguientes:
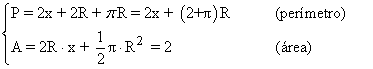
De la ecuación del área obtenemos:
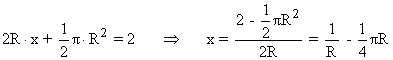
Sustituyendo el valor en la ecuación del perímetro tenemos que:
![]()
Para hallar el valor mínimo del perímetro, calculamos la primera derivada e igualamos a 0:
![]()
Por lo tanto tenemos que:
![]()
Para comprobar que se trata del perímetro mínimo, calculamos la segunda derivada:
![]()
Por lo tanto, las dimensiones de la ventana son:
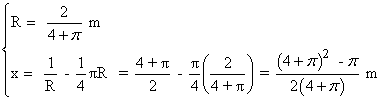
SELECTIVIDAD
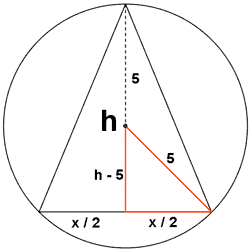
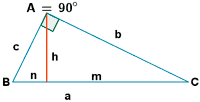
Un triángulo isósceles tiene 10 cm de base (que es el lado desigual) y 20 cm de altura. Se inscribe en este tríangulo un rectángulo uno de cuyos lados se apoya en la base del triángulo. Hallar las dimensiones del rectángulo así construido y que tenga la mayor área posible.
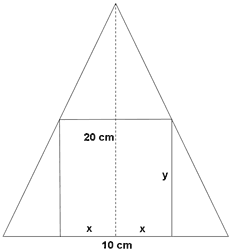
Para calcular el área del rectángulo necesitamos su base y su altura.
Consideraremos su base como: 2x
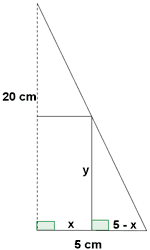
Vamos a encontrar una expresión que describa la altura ' y ' observando la figura de la derecha.
De la semejanza entre triángulos rectángulos se obtiene que:
![]()
Reuniendo dicha expresión y la fórmula del área para el rectángulo tenemos:
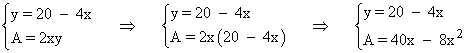
Para encontrar un máximo de la función área tenemos que calcular su derivada e igualarla a 0:
![]()
Comprobamos que es un máximo estudiando el signo de la segunda derivada:
A ''(x) = - 16 < 0 para cualquier valor de x .
Por tanto, x = 5/2 cm maximiza el área del rectángulo.
y = 20 - 4x = 20 - 4(5/2) = 10 cm
Sus dimensiones son: 2x = 5 cm , y = 10 cm
SELECTIVIDAD
El triángulo isósceles descrito en la figura, mide 10 cm. de base y 20 cm. de altura.
a) ¿Cuál es la ecuación de la recta r señalada en la figura que contiene el lado del triángulo?
b) Dado el rectángulo inscrito cuya base mide a , calcula las coordenadas de los puntos B y C en función de a .
c) Halla el valor de a que hace máxima el área del rectángulo.
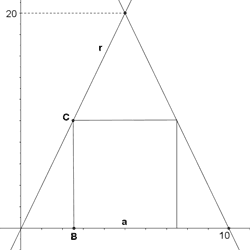
a) ¿Cuál es la ecuación de la recta r señalada en la figura que contiene el lado del triángulo?
Al ser un triángulo isósceles, el vértice superior está situado en el punto que tiene como coordenadas:
y = altura del triángulo = 20
x = mitad de la base = 10/2 = 5
Luego está situado en el punto: (5 , 20)
La recta que nos piden pasa por el origen de coordenadas (0 , 0) y el punto (5 , 20) , luego su pendiente es:
![]()
Por tanto la ecuación de la recta es:
y - y0 = m (x - x0) ⇒ y - 0 = 4 (x - 0) ⇒ y = 4x
b) Dado el rectángulo inscrito cuya base mide a , calcula las coordenadas de los puntos B y C en función de a .
Observamos que la base del rectángulo está centrada con respecto a la base del triángulo. Por lo que el espacio entre el rectángulo y el triángulo isósceles será el mismo por ambos lados.
El punto B tendrá por coordenas:
y = 0
![]()
![]()
La recta BC tiene por ecuación:
![]()
El punto C es el punto de corte de dicha recta con la recta r.
Tenemos que calcular la intersección entre ambas resolviendo el sistema determinado por ambas rectas:
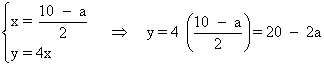
![]()
c) Halla el valor de a que hace máxima el área del rectángulo.
Para determinar el área necesitamos la base y la altura del rectángulo:
h = (coordenada 'y' del punto C ) = 20 - 2a
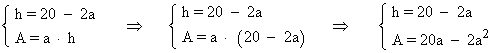
Para hallar el valor máximo del área, calculamos la primera derivada e igualamos a 0 :
A '(a) = 20 - 4a = 0 ⇒ 4a = 20 ⇒ a = 5 cm
Comprobamos que es un máximo de la función área calculando su segunda derivada:
A ''(a) = -4 < 0 para cualquier valor de a
Por tanto, a = 5 cm maximiza el área del rectángulo.
Entre todos los rectángulos inscritos en una circunferencia de radio 12 cm , calcula las dimensiones del que tenga área máxima.
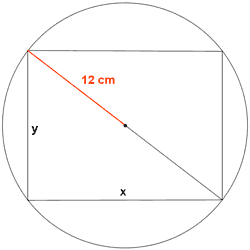
Llamemos x a la base del rectángulo que buscamos e y a la altura.
Puesto que el radio de la circunferencia mide 12 cm , su diámetro medirá: 2·12 = 24
Para establecer una relación entre x e y podemos aplicar el teorema de Pitágoras en el triángulo rectángulo marcado:
![]()
Reuniendo esta condición con la fórmula del área del rectángulo:
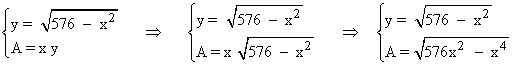
Para encontrar un máximo de la función área tenemos que calcular su derivada e igualarla a 0:
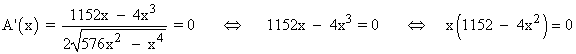
Las soluciones de la ecuación son:
• x = 0 cm
• 1152 - 4x2 = 0 ⇔ x2 = 288 ⇔ x = ± 12√2 cm
Descartamos la solución negativa ya que geométricamente no tiene sentido.
Como queremos que el área del rectángulo sea máxima, no nos iteresa que su base mida x = 0 cm , por tanto, descartamos también dicha solución.
Para confirmar que x = 12√2 cm corresponde a un máximo, calculamos el signo de la primera derivada antes y despues de dicho punto :

Calculamos la altura y :
![]()
Las dimensiones del rectángulo son 12√2 cm y 12√2 cm .
Determine las dimensiones de los lados y el area del rectángulo de área máxima que, teniendo uno de sus lados sobre el diámetro, se puede inscribir en un semicírculo de 2 m de radio.
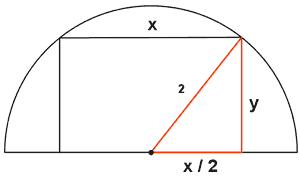
Llamaremos x a su base e y a su altura.
Podemos establecer una relación entre x e y aplicando el teorema de Pitágoras sobre el triángulo marcado en la figura.
La base de dicho triángulo será la mitad de la base del rectángulo.
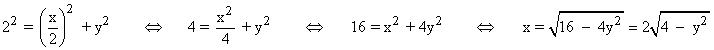
Reuniendo dicha expresión junto con la fórmula del área del rectángulo tenemos:
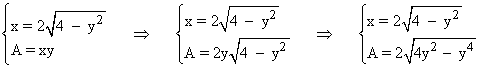
Para encontrar un máximo de la función área tenemos que calcular su derivada e igualarla a 0:
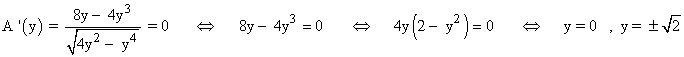
Si y = 0 m. el área del rectángulo será 0 , es decir el área será mínima, por lo que no nos interesa.
También descartamos la solución negativa y = -√2 , puesto que geométricamente no tiene sentido.
Por tanto, y = √2 m. será necesariamente el máximo de la función área del rectángulo.
![]()
Las dimensiones del rectángulo son: √2 m. 2√2 m.
SELECTIVIDAD
En una circunferencia de radio 10 cm, se divide uno de sus diámetros en dos partes que se toman como diámetros de dos circunferencias tangentes interiores a ella. ¿Qué longitud debe tener cada uno de estos dos diámetros para que sea máxima el área delimitada por las tres circunferencias (región sombreada en rojo)?
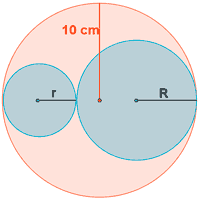
Si r y R son los radios de las circunferencias interiores, se tiene que cumplir que:
20 = 2r + 2R ⇒ 10 = r + R
El área sombreada en rojo vendrá determinada por la diferencia:
A = π102 - πr2 - πR2
Simplificamos la función del area:
A = π(102 - (10 -R)2 - R2) = π(20R - 2R2)
Para encontrar su máximo calculamos su derivada e igualamos a 0 :
A '(R) = 20π - 4πR = 0 ⇒ 4πR = 20π ⇒ 4R = 20 ⇒ R = 5 cm
Comprobamos que es un máximo calculando la segunda derivada:
A ''(R) = - 4π < 0 para cualquier valor de R
Por tanto R = 5 cm maximiza el área sombreada en rojo.
Calculamos r sustituyendo el valor de R en la primera ecuación:
r = 10 + R = 10 + 5 = 5 cm
Los diámetros de ambas circunferencias interiores miden: 2·5 = 10 cm
De los triángulos isósceles inscritos en una circunferencia de radio 5 m , ¿cuál es el de área máxima?
Consideremos x la base del triángulo y h su altura.
Para encontrar una relación entre x y h aplicamos el teorema de Pitágoras en el triángulo marcado en rojo.
base = x/2
altura = h - radio = h - 5
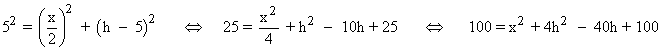
Despejando x:
![]()
Reuniendo dicha expresión y la fórmula del área del triángulo isósceles tenemos:
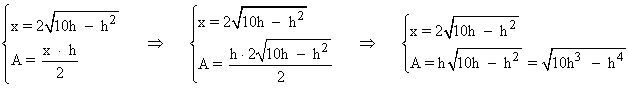
Para encontrar el máximo de la función área calculamos su derivada e igualamos a 0 :
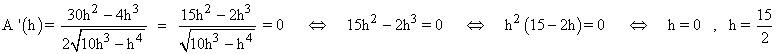
Si h = 0 el área del triángulo será 0 , qué es mínima, por lo que no nos interesa.
Para confirmar que x = 15/2 m corresponde a un máximo, calculamos el signo de la primera derivada antes y despues de dicho punto :
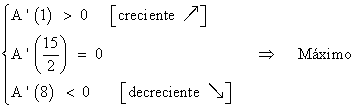
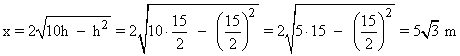
El triángulo deberá medir 15/2 m de base y 5√3 m altura.
Averigua cómo ha de ser un triángulo isósceles de área máxima inscrito en una circunferencia de radio R .
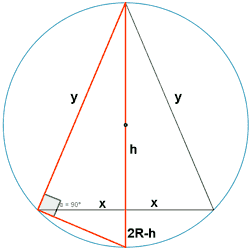
Para determinar el área del triángulo nos hacen falta su base y su altura. LLamemos 2x a su base.
Vamos a encontrar una expresión que describa la altura. Para ello usaremos el teorema de la altura:
Teorema de la altura:
![]()
Aplicamos el teorema de la altura sobre el triángulo marcado en rojo. A la altura de dicho triángulo la hemos llamado 'x' . Entonces:
![]()
Reuniendo dicha expresión y la fórmula del área para el triángulo isósceles tenemos:
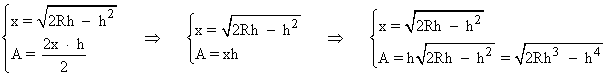
Para encontrar un máximo de la función área calculamos su derivada e igualamos a 0 :
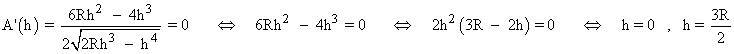
Si tomamos h = 0 el área del triángulo será 0 , que es un mínimo, por lo que no nos interesa.
Puesto que h = 0 es un mínimo de la función, necesariamente h = 3R/2 es un máximo.
La base del triángulo isósceles es 2x , es decir:
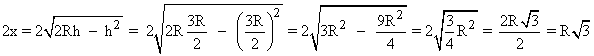
Luego las dimensiones del triángulo son R√3 y 3R/2 .
De los trapecios isósceles inscritos en una circunferencia de radio 5 dm. , ¿cuál es el de área máxima? Se conoce que su base mayor es un diámetro de la circunferencia.
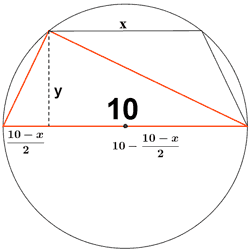
Para determinar el área del trapecio nos hacen falta saber sus bases y su altura.
La base mayor del trapecio se correponde con el diámetro de la circunferencia, luego medirá 10 dm.
Llamaremos a la base menor x .
Vamos a encontrar una expresión que describa la altura ' y ' del trapecio.
Para ello usaremos el teorema de la altura:
Teorema de la altura:
![]()

Aplicamos el teorema de la altura sobre el triángulo marcado en rojo. A la altura de dicho triángulo la hemos llamado ' y ' . Entonces:
![]()
![]()
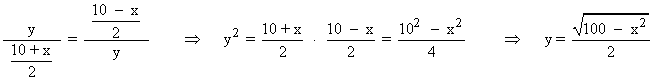
Reuniendo dicha expresión y la fórmula del área para el trapecio isósceles tenemos:
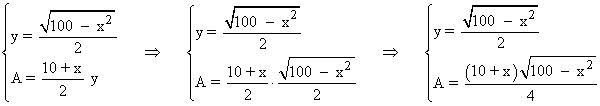
Para encontrar el máximo de la función área calculamos su derivada e igualamos a 0 :

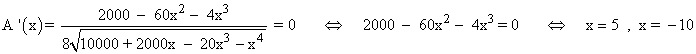
Descartamos la solución negativa, ya que geométricamente no tiene sentido.
Para confirmar que x = 5 dm corresponde a un máximo,  calculamos el signo de la primera derivada antes y despues de dicho punto :
calculamos el signo de la primera derivada antes y despues de dicho punto :
![]()
Las dimensiones del rectángulo serán: 5 dm , 5√3 /2 dm
De todos los rectángulos que se pueden inscribir en una elipse de semiejes 5 y 4 , ¿cuál es el de mayor área?
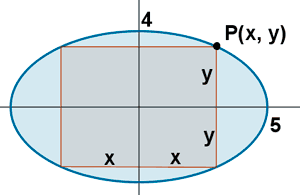
Al tratarse de una elipse, si P(x, y) es el vértice del rectángulo, entonces su área es: A = 2x·2y = 4xy
Además, al ser el vértice un punto de la alipse, sus coordenadas deben cumplir que: (x/a)2 + (y/b)2 = 1
Como los semiejes de la elipse son 5 y 4 tenemos que:
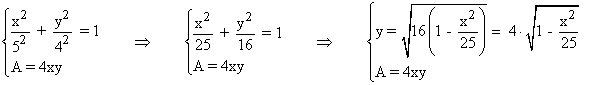
Por lo tanto la función a optimizar es la siguiente:
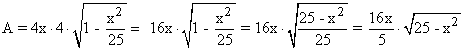
Calculamos la primera derivada e igualamos a 0:
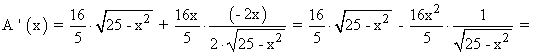
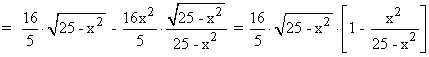
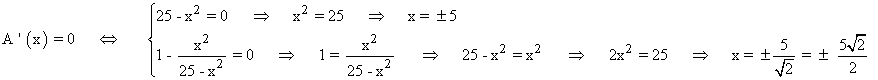
Las soluciones negativas no tienen sentido geométrico, al igual que la solución x = 5 puesto que el cuadrado sería mínimo (correspondería con la línea del eje X).
Por lo tanto la única solución geométricamente posible corresponde a:
![]()
Comprobamos que dicha solución es un máximo de la función A(x) :
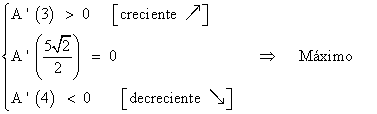
Sustituyendo el valor máximo en la función, tenemos que el área es:
![]()
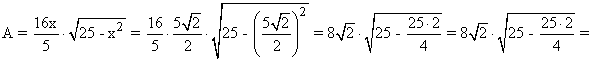


 INICIO
INICIO