Problemas resueltos de aplicaciones de sistemas de ecuaciones I
• Problemas con números:
1) El cajero de un banco solo dispone de billetes de 10, 20 y 50 euros. Hemos sacado 290 € del banco y el cajero ha entregado exactamente 8 billetes. El número de billetes de 19 € que nos ha dado es el doble del de 20 €. Plantee y resuelva el sistema de ecuaciones lineales asociado a este problema para obtener el número de billetes de cada tipo que nos ha entregado el cajero.
2) Luis, Juan y Óscar son tres amigos. Luis le dice a Juan: Si te doy la tercera parte del dinero que tengo, los tres tendremos la misma cantidad. Calcular lo que tiene cada uno de ellos sabiendo que entre los tres reúnen 60 €.
3) En una caja hay monedas de tres tipos: de 2 €, de 1 € y de 50 céntimos. Se sabe que, en total, hay 33 monedas y el valor conjunto de todas ellas es de 40 €. ¿Se puede determinar el número de cada tipo de monedas?
Si la respuesta es afirmativa, encuentra el número de cada uno de los tipos de moneda. Si la respuesta es negativa, encuentra, al menos, dos conjuntos diferentes de 33 monedas de los tipos descritos y de manera que el valor total sea de 40.
• Problemas de cifras:
4) Halla un número de tres cifras sabiendo que estas suman 9; que si al número dado se le resta el que resulta de invertir el orden de sus cifras la diferencia es 198, y que la cifra de las decenas es la media aritmética de las otras dos.
5) Un número capicúa de cinco cifras verifica:
a) La suma de sus cifras es 9
b) La cifra de las centenas es igual a la suma de la de las unidades y de la de las decenas
c) Si se intercambian las cifras de las unidades y de las decenas, el número resultante disminuye en 9
Encuentra el número.
6) Halla un número de tres cifras sabiendo que su suma es 12, que la cifra de las unidades es igual a la semisuma de las cifras de las centenas y de las decenas, y que, por último, el número que resulta al invertir las cifras del buscado es 198 unidades más pequeño que este.
• Problemas de edades:
7) La edad de un padre es el doble de la suma de las edades de sus dos hijos, mientras que hace unos años (exactamente la diferencia de las edades actuales de los hijos), la edad del padre era el triple que la suma de las edades en aquel tiempo de sus hijos. Cuando pasen tantos años como la suma de las edades actuales de los hijos, entre los tres sumarán 150 años. ¿Qué edad tenía el padre cuando nacieron sus hijos?
8) Calcula las edades actuales de una madre y sus dos hijos sabiendo que hace 14 años la edad de la madre era 5 veces la suma de las edades de los hijos, pero que dentro de 10 años la edad de la madre será la suma de las edades que los hijos tengan en ese momento y teniendo en cuenta que cuando el hijo mayor tenga la edad actual de la madre, el hijo menor tendrá 42 años.
9) La suma de las edades actuales de tres hermanos es 63 años. Hace dos años, la edad del mediano era 5 años más que un tercio de la suma de las edades de los otros dos, y dentro de cuatro años, el menor tendrá 9 años más quela quinta parte de la suma de los otros dos. Halla las edades actuales de cada uno de los hermanos.
• Problemas de porcentajes:
10) Dos amigos invierten 20.000 € cada uno. El primero coloca una cantidad A al 4% de interés, una cantidad B al 5% y el resto al 6%. El otro invierte la misma cantidad A al 5%, la B al 6% y el resto al 4%. Determina las cantidades A, B y C sabiendo que el primero obtiene unos intereses de 1.050 € y el segundo de 950 €.
11) Una tienda ha vendido 600 ejemplares de un videojuego por un total de 6.384 €. El precio original era de 12 €, pero también ha vendido copias defectuosas con descuentos del 30% y del 40%. Sabiendo que el número de copias defectuosas vendidas fue la mitad del de copias en buen estado, calcula a cuántas copias se le aplicó el 30% de descuento.
Problemas resueltos de aplicaciones de sistemas de ecuaciones II
1) El cajero de un banco solo dispone de billetes de 10, 20 y 50 euros. Hemos sacado 290 € del banco y el cajero ha entregado exactamente 8 billetes. El número de billetes de 19 € que nos ha dado es el doble del de 20 €. Plantee y resuelva el sistema de ecuaciones lineales asociado a este problema para obtener el número de billetes de cada tipo que nos ha entregado el cajero.
Empezamos asignandolas incógnitas:
x → billetes de 10 y → billetes de 20 z → billetes de 50
De las condiciones, obtenemos el siguiente sistema de ecuaciones:
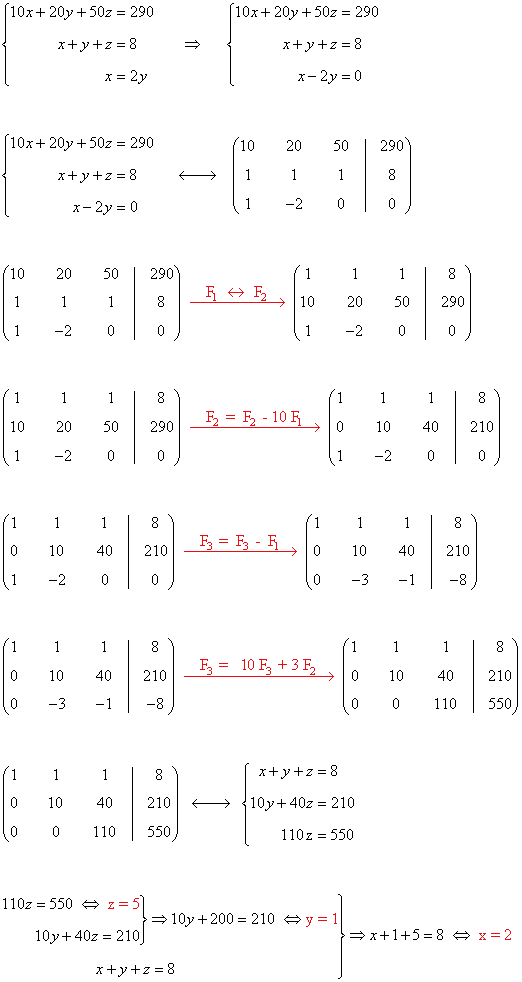
Solución:
Hemos sacado 2 billetes de 10 euros, 1 billete de 20 euros y 5 billetes de 50 euros.
2) Luis, Juan y Óscar son tres amigos. Luis le dice a Juan: Si te doy la tercera parte del dinero que tengo, los tres tendremos la misma cantidad. Calcular lo que tiene cada uno de ellos sabiendo que entre los tres reúnen 60 €.
Empezamos asignandolas incógnitas:
x → dinero de Luis y → dinero de Juán z → dinero de Óscar
De las condiciones, obtenemos el siguiente sistema de ecuaciones:
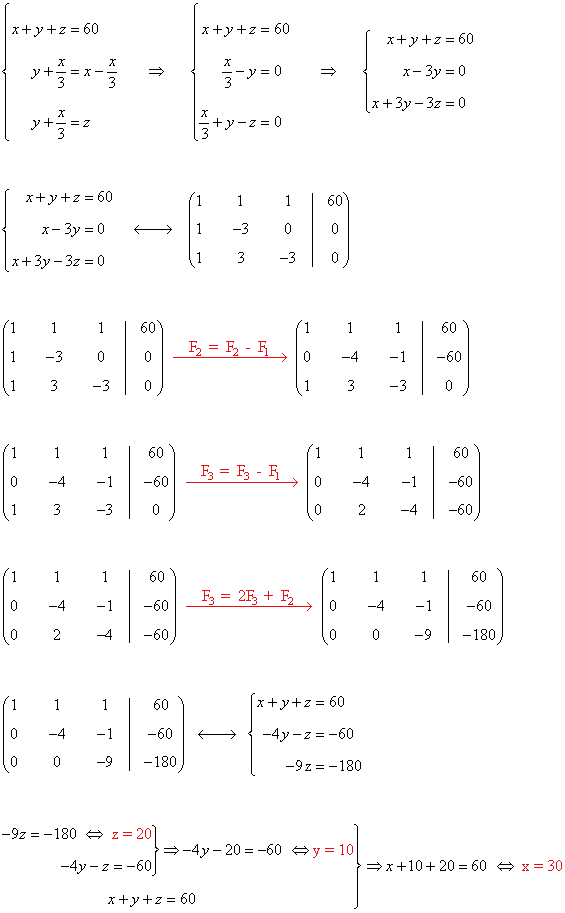
Solución:
Óscar tiene 20 euros, Juan tiene 10 euros y Luis tiene 30 euros.
3) En una caja hay monedas de tres tipos: de 2 €, de 1 € y de 50 céntimos. Se sabe que, en total, hay 33 monedas y el valor conjunto de todas ellas es de 40 €. ¿Se puede determinar el número de cada tipo de monedas?
Si la respuesta es afirmativa, encuentra el número de cada uno de los tipos de moneda. Si la respuesta es negativa, encuentra, al menos, dos conjuntos diferentes de 33 monedas de los tipos descritos y de manera que el valor total sea de 40.
Empezamos asignandolas incógnitas:
x → número de monedas de 1 € y → número de monedas de 1 € z → número de monedas de 50 céntimos
De las condiciones, obtenemos el siguiente sistema de ecuaciones:
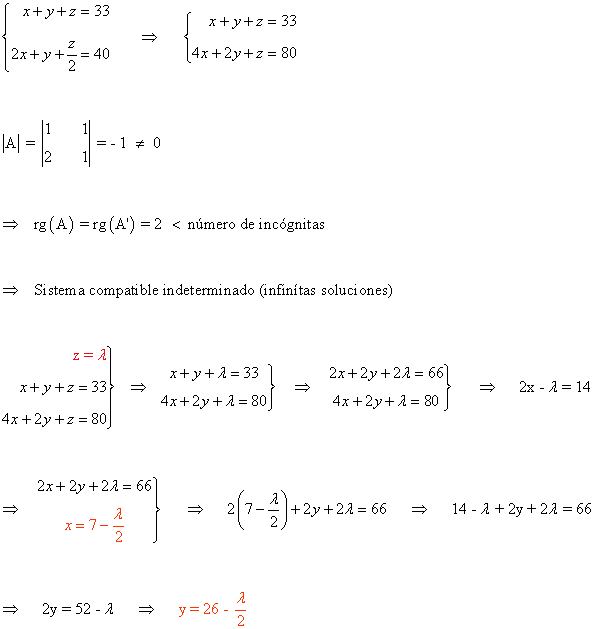
Dos posibles soluciones serían:
• 8 monedas de 2 €, 23 monedas de 1 € y 2 monedas de 50 céntimos.
• 2 monedas de 2 €, 21 monedas de 1 € y 10 monedas de 50 céntimos.
4) Halla un número de tres cifras sabiendo que estas suman 9; que si al número dado se le resta el que resulta de invertir el orden de sus cifras la diferencia es 198, y que la cifra de las decenas es la media aritmética de las otras dos.
- Traducir al lenguaje algebraico el enunciado:
- Calcular las soluciones empleando las herramientas algebraicas:
- Comprobar las soluciones obtenidas:
Empezamos asignando a cada una de las cifras una incógnita, ya que son los valores que queremos determinar. Llamamos
x → unidades y → decenas z → centenas
Nos dicen que estas cifras suman 9, es decir
x + y + z = 9
Que si al número dado se le resta el que resulta de invertir el orden de sus cifras la diferencia es 198, es decir,
100z + 10y + x - (100x + 10y + z) = 198
y que la cifra de las decenas es la media aritmética de las otras dos, es decir,![]()
Reuniendo las tres ecuaciones el número que queremos determinar será el que tenga por cifras a las soluciones del siguiente sistema de ecuaciones:
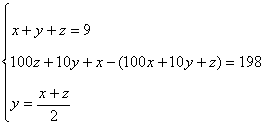
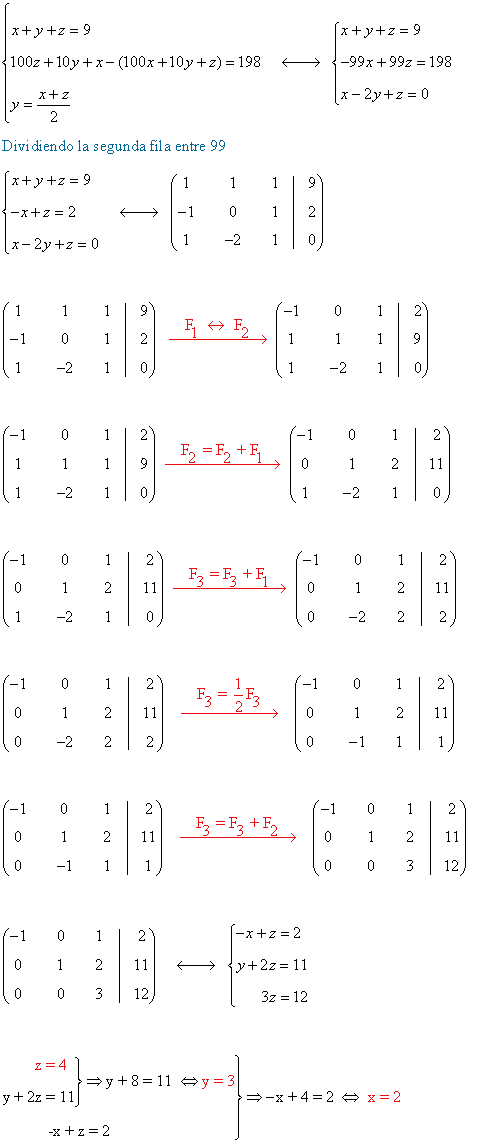
Esta solución tiene sentido, ya que se nos pedía determinar las cifras de un número de tres cifras y dichas cifras deben ser números naturales entre 0 y 9.
El número que queríamos determinar es el 432.
5) Un número capicúa de cinco cifras verifica:
a) La suma de sus cifras es 9
b) La cifra de las centenas es igual a la suma de la de las unidades y de la de las decenas
c) Si se intercambian las cifras de las unidades y de las decenas, el número resultante disminuye en 9
Encuentra el número.
- Traducir al lenguaje algebraico el enunciado:
- Calcular las soluciones empleando las herramientas algebraicas:
- Comprobar las soluciones obtenidas:
Empezamos asignando a cada una de las cifras una incógnita, ya que son los valores que queremos determinar. Llamamos
x → decena de millar y → millar z → centenas y → decenas x → unidades
Nos dicen que estas cifras suman 9, es decir:
x + y + z + y + z = 9
2x + 2y + z = 9
Que la cifra de las centenas es igual a la suma de las unidades y las decenas, es decir:
x + y - z = 0
Y que si se intercambian las cifras de las unidades y de las decenas, el número resultante disminuye en 9:
104x + 103y + 102z + 10y + x = 104x + 103y + 102z + 10x + y + 9
x - y = -1
Reuniendo las tres ecuaciones el número que queremos determinar será el que tenga por cifras a las soluciones del siguiente sistema de ecuaciones:
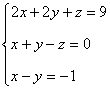
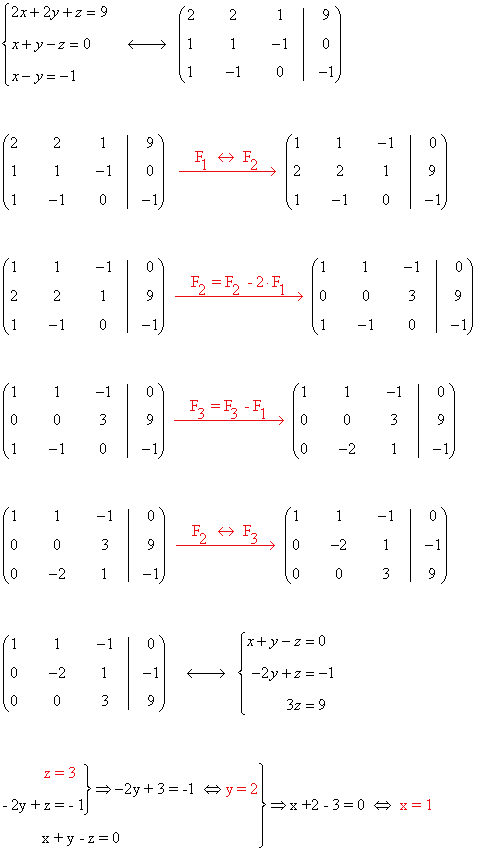
La solución al sistema es (1, 2, 3), por lo que el número es: 12.321
Esta solución tiene sentido, puesto que buscábamos tres cifras para un número capicúa de cinco cifras. El número que queríamos determinar es el 12.321
6) Halla un número de tres cifras sabiendo que su suma es 12, que la cifra de las unidades es igual a la semisuma de las cifras de las centenas y de las decenas, y que, por último, el número que resulta al invertir las cifras del buscado es 198 unidades más pequeño que este.
- Traducir al lenguaje algebraico el enunciado:
- Calcular las soluciones empleando las herramientas algebraicas:
- Comprobar las soluciones obtenidas:
Empezamos asignando a cada una de las cifras una incógnita, ya que son los valores que queremos determinar. Llamamos
z → centenas y → decenas x → unidades
Nos dicen que estas cifras suman 9, es decir
x + y + z = 12
Que la cifra de las unidades es igual a la semisuma de las centenas y las decenas:
y que la cifra de las decenas es la media aritmética de las otras dos, es decir,
![]()
y que el número que resulta al invertir las cifras buscado es 198 unidades más pequeño que este:
100x + 10y + z = 100z +10y + x + 198
Reuniendo las tres ecuaciones el número que queremos determinar será el que tenga por cifras a las soluciones del siguiente sistema de ecuaciones:
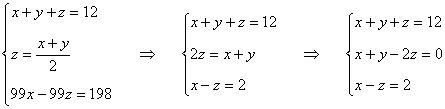
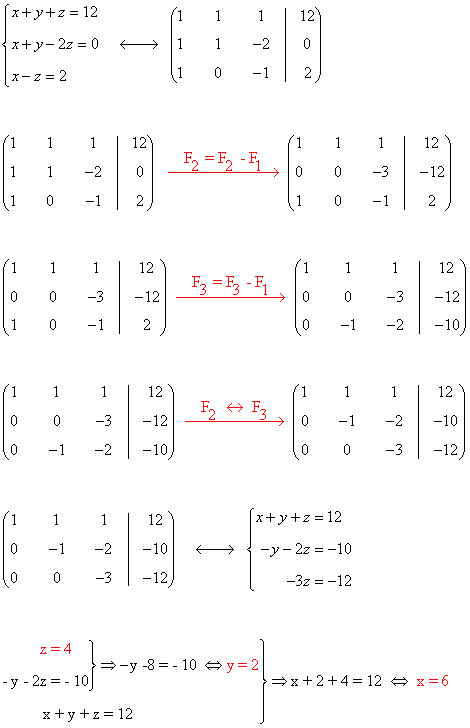
Esta solución tiene sentido, ya que se nos pedía determinar las cifras de un número de tres cifras y dichas cifras deben ser números naturales entre 0 y 9.
El número que queríamos determinar es el 624.
7) La edad de un padre es el doble de la suma de las edades de sus dos hijos, mientras que hace unos años (exactamente la diferencia de las edades actuales de los hijos), la edad del padre era el triple que la suma de las edades en aquel tiempo de sus hijos. Cuando pasen tantos años como la suma de las edades actuales de los hijos, entre los tres sumarán 150 años. ¿Qué edad tenía el padre cuando nacieron sus hijos?
Vamos a hacer una tabla que nos va a facilitar traducir al álgebra el problema que nos plantean:
Edad actual |
Edad hace y - z años |
Edad dentro de y + z años |
|
|---|---|---|---|
| Padre | x |
x - (y - z) = x - y + z |
x + (y+z) = x + y + z |
| Primer hijo | y |
y - (y - z) = z |
y + (y + z) = 2y + z |
| Segundo hijo | z |
z - (y - z) = -y + 2z |
z + (y + z) = y + 2z |
Teniendo en cuenta esta tabla es fácil obtener las ecuaciones que nos permiten resolver el problema:
- La edad de un padre es el doble de la suma de las edades de sus dos hijos: En este caso se nos habla de edad actual. Nos fijamos en la columna de edades actuales. La ecuación sería la siguiente:

- Hace unos años (exactamente la diferencia de las edades actuales de los hijos), la edad del padre era el triple que la suma de las edades en aquel tiempo de sus hijos: En este caso nos fijamos en las respectivas edades que vienen dadas por la segunda columna. La ecuación sería la siguiente:
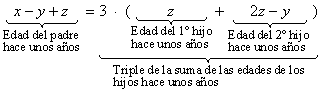
- Cuando pasen tantos años como la suma de las edades actuales de los hijos, entre los tres sumarán 150 años: En este caso consideramos la información de la tercera columna de la matriz. La ecuación que obtenemos es la siguiente:

Bastará por tanto que resolvamos el siguiente sistema de ecuaciones:
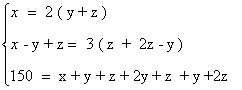
Aplicamos Gauss:
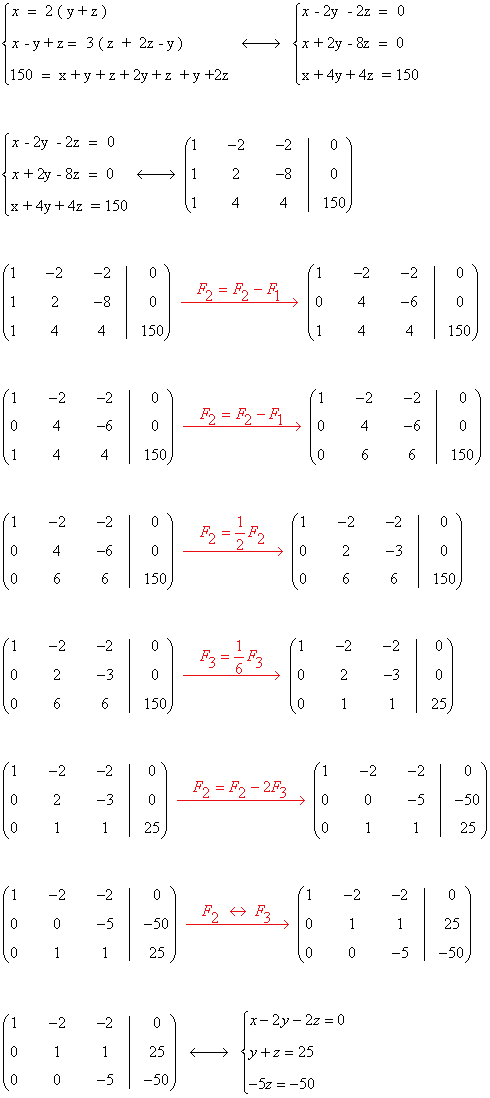
Resolvemos el sistema equivalente:
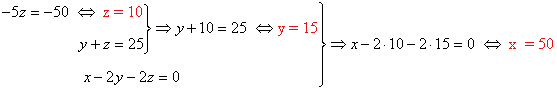
Actualmente el padre tiene 50 años, el primer hijo 15 y el segundo hijo 10.
La solución del sistema no es la respuesta a la pregunta que nos plantea el problema ya que nos piden la edad del padre cuando nacieron cada uno de sus hijos.
Solución:
- El padre tenía 35 años cuando nació su primer hijo, ya que actualmente tiene 50 años y el primer hijo nació hace 15.
- El padre tenía 40 cuando nació el segundo hijo, ya que actualmente tiene 50 años y su segundo hijo nació hace 10.
8) Calcula las edades actuales de una madre y sus dos hijos sabiendo que hace 14 años la edad de la madre era 5 veces la suma de las edades de los hijos, pero que dentro de 10 años la edad de la madre será la suma de las edades que los hijos tengan en ese momento y teniendo en cuenta que cuando el hijo mayor tenga la edad actual de la madre, el hijo menor tendrá 42 años.
Vamos a traducir al lenguaje algebráico las condiciones que nos da el problema, donde x es la edad de la madre, y la del hijo mayor y z la del hijo menor:
- La edad de la madre hace 14 años era 5 veces la suma de las edades de los hijos.
x - 14 = 5(y - 14 + z - 14)
- Dentro de 10 años la edad de la madre será la suma de las edades que los hijos tengan en ese momento.
x + 10 = y + 10 + z + 10
- Cuando el hijo mayor tenga la edad actual de la madre, el hijo menor tendrá 42 años.
z + x - y = 42
Bastará por tanto que resolvamos el siguiente sistema de ecuaciones:
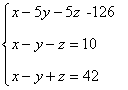
Aplicamos Gauss:
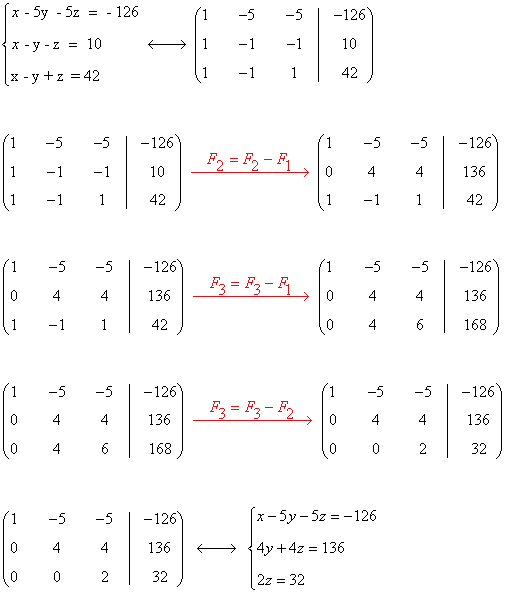
Resolvemos el sistema equivalente:
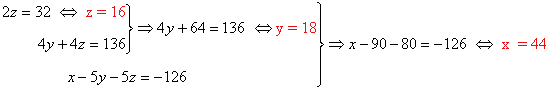
Solución:
Actualmente la madre tiene 44 años, el primer hijo 18 y el segundo hijo 16.
9) La suma de las edades actuales de tres hermanos es 63 años. Hace dos años, la edad del mediano era 5 años más que un tercio de la suma de las edades de los otros dos, y dentro de cuatro años, el menor tendrá 9 años más quela quinta parte de la suma de los otros dos. Halla las edades actuales de cada uno de los hermanos.
Empezamos asignando a cada uno de los hijos una incógnita, ya que son los valores que queremos determinar:
x→ hijo mayor y → hijo mediano z → hijo menor
Traducimos al lenguaje algebráico las condiciones que nos da el problema:
- La suma de las edades de los tres hermanos es 63 años.
x + y + z = 63
- Hace dos años, la edad del mediano era 5 años más que un tercio de la suma de las edades de los otros dos.
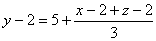
- Cuando pasen tantos años como la suma de las edades actuales de los hijos, la suma de las edades de las tres personas será 150 años:.
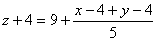
Bastará por tanto que resolvamos el siguiente sistema de ecuaciones:
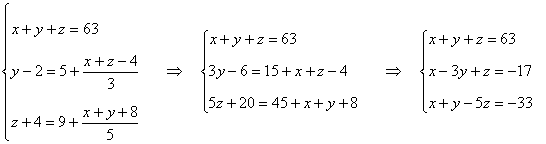
Aplicamos Gauss:
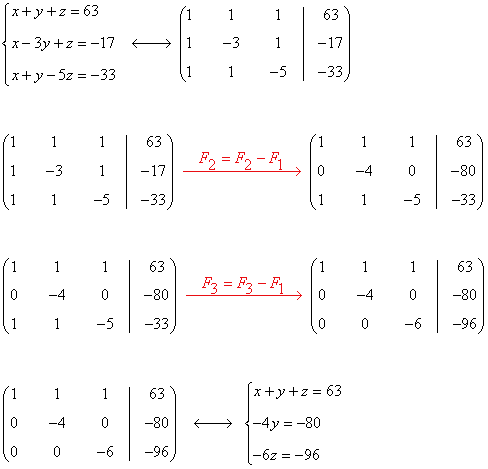
Resolvemos el sistema equivalente:
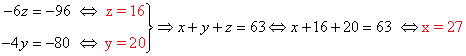
Solución:
Las edades de los tres hermanos son 27, 20 y 16 años.
10) Dos amigos invierten 20.000 € cada uno. El primero coloca una cantidad A al 4% de interés, una cantidad B al 5% y el resto al 6%. El otro invierte la misma cantidad A al 5%, la B al 6% y el resto al 4%. Determina las cantidades A, B y C sabiendo que el primero obtiene unos intereses de 1.050 € y el segundo de 950 €.
Vamos a traducir al lenguaje algebráico las condiciones que nos da el problema:
- Dos amigos invierten 20.000 €.
A + B + C = 20.000
- El primero coloca una cantidad A al 4%, B al 5% y el resto al 6%, con unos intereses de 1.050 €.
(4/100)A + (5/100)B + (6/100)C = 1.050
- El segundo coloca una cantidad A al 5%, B al 6% y el resto al 4%, con unos intereses de 950 €.
(5/100)A + (6/100)B + (4/100)C = 950
Bastará por tanto que resolvamos el siguiente sistema de ecuaciones:
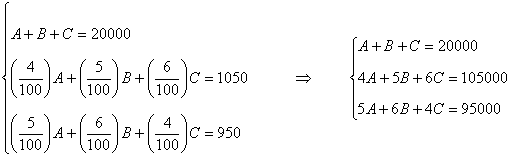
Aplicamos Gauss:
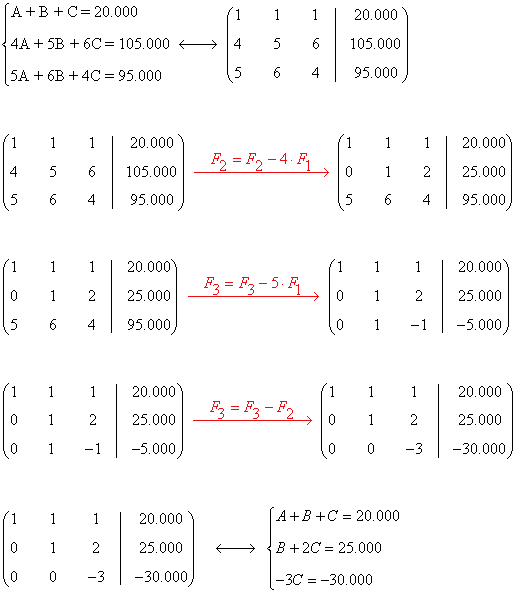
Resolvemos el sistema equivalente:
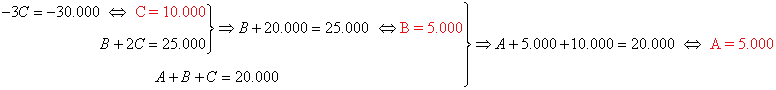
Solución:
Por lo tanto la cantidad A es de 5.000 €, la cantidad B también 5.000 € y la cantidad C asciende a 10.000 €.
11) Una tienda ha vendido 600 ejemplares de un videojuego por un total de 6.384 €. El precio original era de 12 €, pero también ha vendido copias defectuosas con descuentos del 30% y del 40%. Sabiendo que el número de copias defectuosas vendidas fue la mitad del de copias en buen estado, calcula a cuántas copias se le aplicó el 30% de descuento.
Vamos a llamar x al número de copias vendidas al precio original (12€), y al número de copias vendidas con un 30% de descuento (8,4 €), y z al número de copias vendidas con un 40% de descuento (7,2 €). Y a continuación traducimos el enunciado a lenguaje algebráico:
- La tienda ha vendido 600 copias..
x + y + z = 600
- La facturación total ha sido de 6.384 €.
12x + 8,4y + 7,2z = 6.384
- El número de copias defectuosas vendidas fue la mitad del de copias en buen estado.
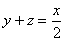
Bastará por tanto que resolvamos el siguiente sistema de ecuaciones:
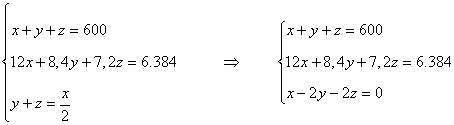
Aplicamos Gauss:
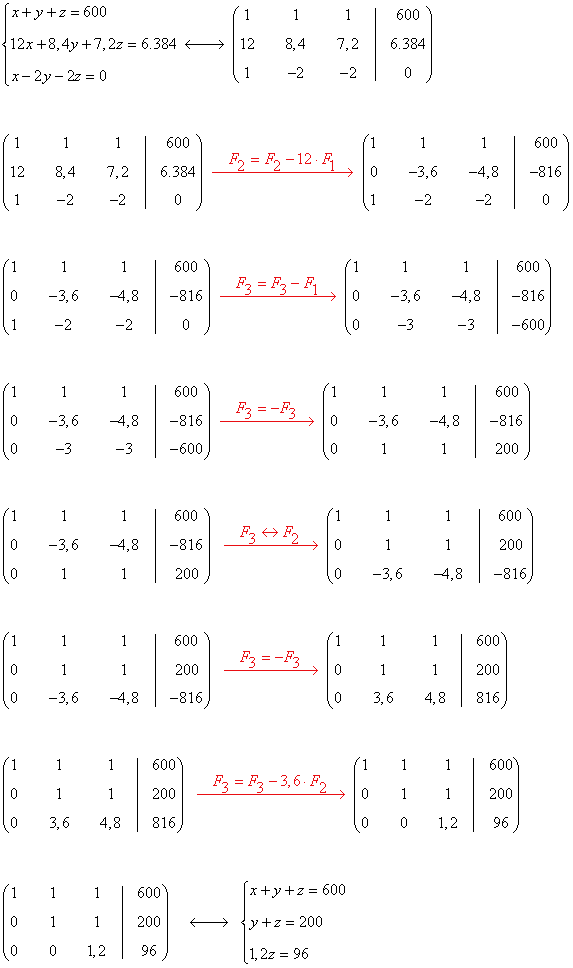
Resolvemos el sistema equivalente:
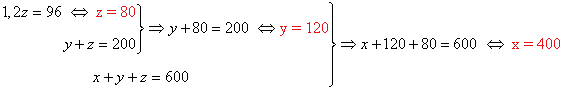
Solución:
Por lo tanto el 30% de descuento se le aplicó a 120 copias del videojuego.


 INICIO
INICIO